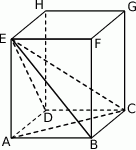
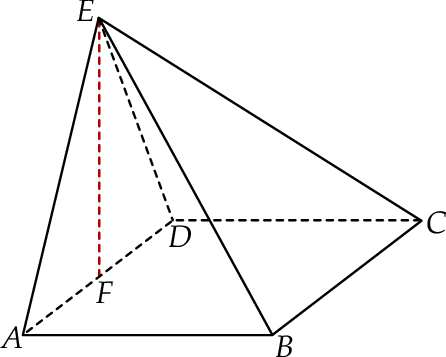
Podstawą ostrosłupa 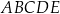 jest kwadrat o boku długości 12. Spodek
jest kwadrat o boku długości 12. Spodek 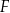 wysokości
wysokości 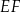 ostrosłupa jest środkiem krawędzi
ostrosłupa jest środkiem krawędzi 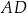 . Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi
. Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi 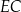 do płaszczyzny podstawy.
do płaszczyzny podstawy.

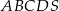 jest prostokąt
jest prostokąt 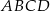 , w którym
, w którym 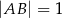 ,
, 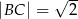 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.
. Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa. 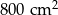 , a kąt ostry rombu ma miarę
, a kąt ostry rombu ma miarę 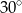 . Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:
. Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz: 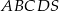 jest czworokąt
jest czworokąt 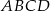 . Przekątna
. Przekątna 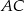 tego czworokąta ma długość
tego czworokąta ma długość 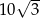 , a kąt
, a kąt 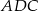 ma miarę
ma miarę 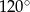 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 26. Oblicz odległość środka wysokości tego ostrosłupa od krawędzi 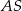 .
. 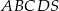 jest czworokąt
jest czworokąt 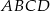 . Przekątna
. Przekątna 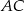 tego czworokąta ma długość
tego czworokąta ma długość 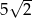 , a kąt
, a kąt 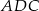 ma miarę
ma miarę 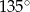 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 13. Oblicz sumę odległości spodka wysokości ostrosłupa od krawędzi bocznych 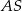 ,
, 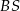 ,
, 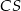 i
i 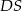 .
. 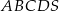 jest równoległobok
jest równoległobok 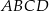 o przekątnej długości
o przekątnej długości 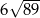 i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku
i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku 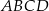 , a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa
, a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa 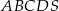 .
. 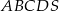 jest romb
jest romb 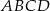 . Krawędź
. Krawędź 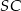 jest prostopadła do płaszczyzny podstawy, krawędź
jest prostopadła do płaszczyzny podstawy, krawędź 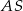 ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem
ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 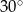 . Krawędź
. Krawędź 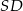 ma długość
ma długość 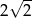 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 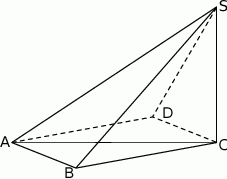
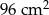 kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 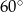 . Oblicz pole powierzchni całkowitej tej bryły.
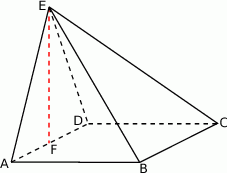
. Oblicz pole powierzchni całkowitej tej bryły. 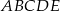 jest kwadrat
jest kwadrat 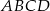 . Punkt
. Punkt 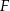 jest środkiem krawędzi
jest środkiem krawędzi 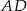 , odcinek
, odcinek 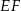 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że 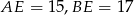 .
. 
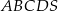 jest trapez
jest trapez 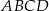 . Przekątna
. Przekątna 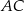 tego trapezu ma długość
tego trapezu ma długość 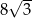 , jest prostopadła do ramienia
, jest prostopadła do ramienia 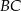 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 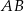 tego trapezu kąt o mierze
tego trapezu kąt o mierze 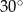 . Każda krawędź boczna tego ostrosłupa ma tę samą długość
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 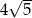 . Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 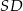 .
. 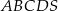 jest trapez
jest trapez 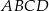 . Przekątna
. Przekątna 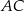 tego trapezu ma długość
tego trapezu ma długość 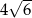 , jest prostopadła do ramienia
, jest prostopadła do ramienia 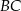 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 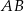 tego trapezu kąt o mierze
tego trapezu kąt o mierze 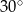 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 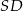 .
. 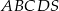 jest prostokąt
jest prostokąt 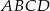 . Spodkiem wysokości ostrosłupa jest środek
. Spodkiem wysokości ostrosłupa jest środek 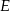 krawędzi
krawędzi 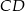 . Oblicz tangens kąta między ścianami bocznymi
. Oblicz tangens kąta między ścianami bocznymi 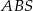 i
i 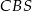 tego ostrosłupa jeżeli
tego ostrosłupa jeżeli 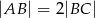 i
i 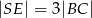 .
. 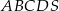 jest trapez równoramienny
jest trapez równoramienny 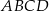 , którego ramiona mają długość
, którego ramiona mają długość 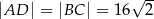 i tworzą z podstawą
i tworzą z podstawą 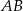 kąt ostry o mierze
kąt ostry o mierze 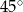 . Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem
. Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem  takim, że
takim, że 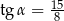 . Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej 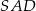 .
. 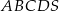 jest trapez
jest trapez 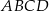 (
(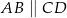 ). Ramiona tego trapezu mają długości
). Ramiona tego trapezu mają długości 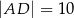 i
i 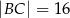 , a miara kąta
, a miara kąta 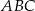 jest równa
jest równa 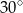 . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt  , taki, że
, taki, że 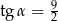 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 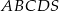 jest prostokąt
jest prostokąt 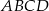 o bokach długości
o bokach długości 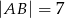 i
i 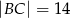 . Krawędź
. Krawędź 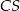 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 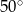 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość. 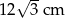 , a spodek
, a spodek 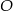 tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 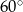 .
. 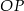 , którego długość jest równa odległości punktu
, którego długość jest równa odległości punktu 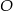 od ściany bocznej.
od ściany bocznej. 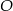 od ściany bocznej.
od ściany bocznej.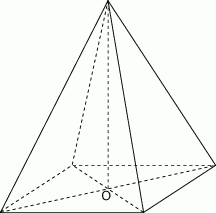
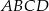 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 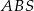 ,
, 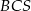 ,
, 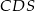 i
i 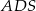 są odpowiednio równe: 740,
są odpowiednio równe: 740, 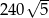 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa. 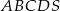 jest kwadrat
jest kwadrat 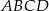 o boku długości 4. Odcinek
o boku długości 4. Odcinek 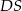 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 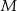 jest środkiem odcinka
jest środkiem odcinka 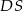 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 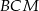 .
. 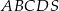 jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość
jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 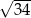 . Krawędź
. Krawędź 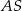 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 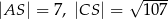 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 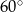 . Oblicz pole powierzchni ostrosłupa.
. Oblicz pole powierzchni ostrosłupa. 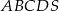 jest kwadrat
jest kwadrat 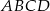 . Trójkąt równoramienny
. Trójkąt równoramienny 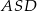 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 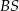 ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną
ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 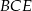 , gdzie
, gdzie 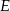 jest środkiem krawędzi
jest środkiem krawędzi 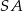 .
. 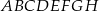 przekątna
przekątna 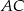 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 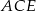 jest równy
jest równy 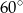 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 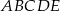 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.