W trójkącie 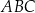 dane są długości dwóch boków
dane są długości dwóch boków 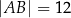 ,
, 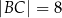 oraz miara kąta
oraz miara kąta 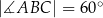 . Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
. Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Długości odcinków
W trójkącie 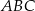 dane są kąt
dane są kąt 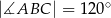 ,
, 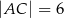 i
i 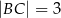 . Dwusieczna kąta
. Dwusieczna kąta 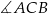 przecina bok
przecina bok 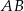 w punkcie
w punkcie 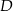 . Oblicz długość odcinka
. Oblicz długość odcinka 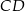 .
.
W trójkącie ostrokątnym 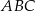 wysokości
wysokości 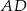 i
i 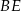 przecinają się w punkcie
przecinają się w punkcie 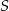 . Wiadomo, że
. Wiadomo, że 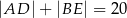 ,
, 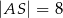 ,
, 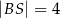 . Wyznacz długości odcinków
. Wyznacz długości odcinków 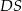 i
i 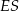 .
.
W trójkącie 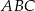 bok
bok 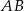 ma długość 8, a bok
ma długość 8, a bok 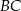 ma długość 10. Dwusieczna kąta
ma długość 10. Dwusieczna kąta 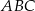 przecina bok
przecina bok 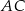 w punkcie
w punkcie 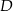 takim, że
takim, że 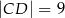 (zobacz rysunek).
(zobacz rysunek).
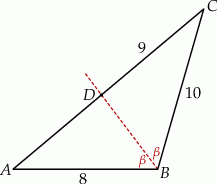
Oblicz długość odcinka 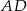 .
.
Na wysokości 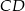 trójkąta
trójkąta 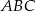 wybrano punkt
wybrano punkt 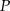 taki, że
taki, że 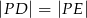 , gdzie
, gdzie 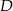 i
i 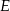 są rzutami tego punktu odpowiednio na boki
są rzutami tego punktu odpowiednio na boki 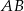 i
i 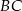 . Wiedząc, że
. Wiedząc, że 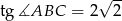 oblicz iloraz
oblicz iloraz  .
.
W okrąg o promieniu 4 wpisano trójkąt 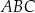 . Długość boku
. Długość boku 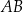 jest równa 6. Bok
jest równa 6. Bok 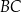 ma długość
ma długość 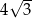 i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku
i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku 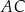 trójkąta
trójkąta 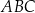 .
.
Trójkąt 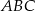 podzielony jest przez dwie proste równoległe do boku
podzielony jest przez dwie proste równoległe do boku 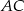 , na trzy figury o równych polach. Oblicz na jakie części proste te podzieliły bok
, na trzy figury o równych polach. Oblicz na jakie części proste te podzieliły bok 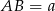 .
.
W trójkącie ostrokątnym 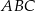 bok
bok 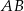 ma długość 18 cm, a wysokość
ma długość 18 cm, a wysokość 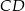 jest równa 15 cm. Punkt
jest równa 15 cm. Punkt 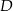 dzieli bok
dzieli bok 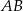 tak, że
tak, że 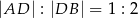 . Przez punkt
. Przez punkt 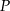 leżący na odcinku
leżący na odcinku 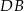 poprowadzono prostą równoległą do prostej
poprowadzono prostą równoległą do prostej 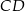 , odcinając od trójkąta
, odcinając od trójkąta 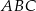 trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta
trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta 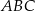 . Oblicz długość odcinka
. Oblicz długość odcinka 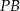 .
.
W trójkącie 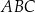 , w którym
, w którym 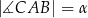 , poprowadzono dwusieczną
, poprowadzono dwusieczną 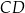 kąta wewnętrznego
kąta wewnętrznego 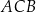 , przy czym
, przy czym 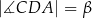 . Oblicz
. Oblicz 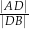 .
.
Oblicz sumę długości środkowych trójkąta o długościach boków: 2, 3 i 4.
Na trójkącie o bokach długości 15, 20, 25 opisano okrąg. Oblicz długość środkowej tego trójkąta poprowadzonej do środka najdłuższego boku.
W trójkącie 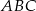 dane są:
dane są: 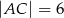 ,
, 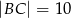 i kąt
i kąt 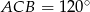 . Wyznacz długość środkowej
. Wyznacz długość środkowej 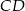 tego trójkąta.
tego trójkąta.
W trójkącie 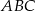 wysokość
wysokość 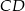 dzieli bok
dzieli bok 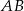 na odcinki długości
na odcinki długości 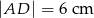 i
i 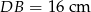 . Bok
. Bok 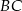 ma 20 cm długości. Poprowadzono symetralną boku
ma 20 cm długości. Poprowadzono symetralną boku 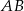 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 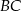 .
.
W trójkącie 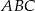 wysokość
wysokość 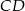 dzieli bok
dzieli bok 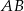 na odcinki długości
na odcinki długości 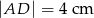 i
i 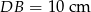 . Bok
. Bok 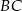 ma 16 cm długości. Poprowadzono symetralną boku
ma 16 cm długości. Poprowadzono symetralną boku 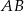 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 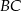 .
.
Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?
W trójkącie 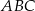 dane są długości boków:
dane są długości boków: 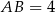 ,
, 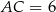 ,
, 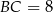 . Oblicz długości odcinków, na jakie dzieli bok
. Oblicz długości odcinków, na jakie dzieli bok 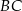 wysokość opuszczona z wierzchołka
wysokość opuszczona z wierzchołka 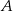 .
.
Na trójkącie 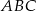 , w którym
, w którym 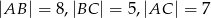 opisano okrąg o środku
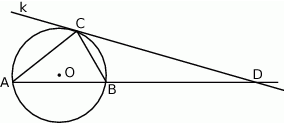
opisano okrąg o środku 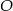 . Następnie poprowadzono styczną
. Następnie poprowadzono styczną 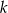 do okręgu w punkcie
do okręgu w punkcie 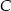 , która w punkcie
, która w punkcie 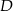 przecięła prostą zawierającą bok
przecięła prostą zawierającą bok 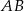 (jak na rysunku poniżej). Oblicz odległość punktu
(jak na rysunku poniżej). Oblicz odległość punktu 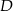 od wierzchołka
od wierzchołka 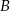 , jeżeli wiadomo, że
, jeżeli wiadomo, że 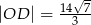 .
.
W trójkącie 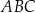 symetralna boku
symetralna boku 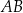 dzieli bok
dzieli bok 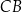 na odcinki długości
na odcinki długości 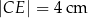 i
i 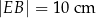 . Bok
. Bok 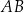 ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość
ma 16 cm długości. Wyznacz długości odcinków, na jakie wysokość 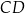 podzieliła bok
podzieliła bok 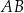 .
.

