Wyznacz te wartości parametru  , dla których zbiorem rozwiązań nierówności
, dla których zbiorem rozwiązań nierówności 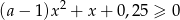 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
/Szkoła średnia/Nierówności/Kwadratowe/Z parametrem
Znajdź wszystkie wartości 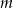 , dla których funkcja
, dla których funkcja 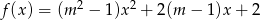 przyjmuje wartość dodatnią dla każdej liczby rzeczywistej
przyjmuje wartość dodatnią dla każdej liczby rzeczywistej  .
.
Dana jest nierówność kwadratowa z parametrem 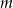 :
: 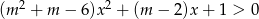 . Dla jakich wartości parametru
. Dla jakich wartości parametru 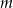 nierówność jest spełniona przez każdą liczbę rzeczywistą?
nierówność jest spełniona przez każdą liczbę rzeczywistą?
Funkcja 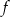 każdej liczbie naturalnej dodatniej
każdej liczbie naturalnej dodatniej  przyporządkowuje liczbę wszystkich liczb naturalnych należących do zbioru rozwiązań nierówności
przyporządkowuje liczbę wszystkich liczb naturalnych należących do zbioru rozwiązań nierówności 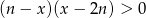 z niewiadomą
z niewiadomą  . Napisz wzór funkcji
. Napisz wzór funkcji 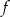 i narysuj jej wykres dla
i narysuj jej wykres dla 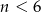 .
.
Dla jakich wartości parametru 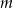 funkcja
funkcja
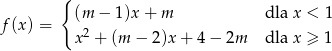
przyjmuje tylko dodatnie wartości?
Dla jakich wartości parametru  zbiór rozwiązań nierówności
zbiór rozwiązań nierówności 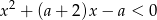 jest niepusty i należą do niego tylko liczby ujemne?
jest niepusty i należą do niego tylko liczby ujemne?
Dla jakich wartości parametru  zbiór rozwiązań nierówności
zbiór rozwiązań nierówności 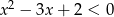 jest zawarty w zbiorze rozwiązań nierówności
jest zawarty w zbiorze rozwiązań nierówności 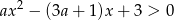 ?
?
Dla jakich wartości parametru 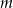 nierówność
nierówność 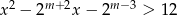 jest prawdziwa dla każdej liczby rzeczywistej.
jest prawdziwa dla każdej liczby rzeczywistej.
Dla jakich wartości parametru 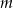 wartości funkcji
wartości funkcji 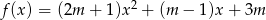 są dla każdego argumentu
są dla każdego argumentu  mniejsze od odpowiednich wartości funkcji
mniejsze od odpowiednich wartości funkcji 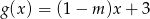 ?
?
Znajdź wszystkie wartości parametru 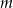 , dla których zbiór
, dla których zbiór 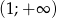 zawiera się w zbiorze rozwiązań nierówności
zawiera się w zbiorze rozwiązań nierówności 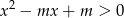 .
.
Rozwiązaniem nierówności 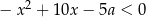 jest zbiór
jest zbiór 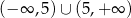 . Wyznacz
. Wyznacz  .
.
Wyznacz wszystkie wartości  , dla których nierówność
, dla których nierówność 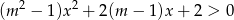 jest prawdziwa dla każdego
jest prawdziwa dla każdego 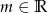 .
.
Wyznacz wszystkie wartości 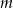 , dla których nierówność
, dla których nierówność 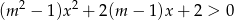 jest prawdziwa dla każdego
jest prawdziwa dla każdego 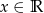 .
.
Wyznacz te wartości parametru 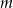 , dla których nierówność
, dla których nierówność 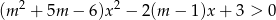 jest prawdziwa dla każdego
jest prawdziwa dla każdego 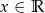 .
.
Wyznacz te wartości parametru 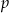 , dla których nierówność
, dla których nierówność 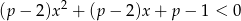 nie ma rozwiązań.
nie ma rozwiązań.

