W wyborach na przewodniczącego klasy kandydowało troje uczniów: Jacek, Helena i Grzegorz. Każdy uczeń tej klasy oddał jeden ważny głos. Jacek otrzymał 9 głosów, co stanowiło 36% wszystkich głosów. Helena otrzymała o 6 głosów więcej niż Grzegorz. Oblicz, ile głosów otrzymała Helena, a ile – Grzegorz.
/Szkoła podstawowa/Zadania z treścią/Liczba osób
Ukryj
Podobne zadania
W maratonie czytelniczym rywalizowało troje uczniów: Kasia, Ela i Romek. Kasia przeczytała 11 książek, co stanowiło 44% wszystkich książek przeczytanych przez te 3 osoby. Romek przeczytał o 4 książki mniej od Eli. Oblicz, ile książek przeczytał Romek, a ile – Ela.
Uczniowie klas trzecich pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było ośmioro uczniów. Jeśli w każdym przedziale byłoby sześcioro uczniów, to zajęliby oni o 3 przedziały więcej. Ilu uczniów pojechało na tę wycieczkę? Zapisz obliczenia.
Ukryj
Podobne zadania
Uczniowie klas pierwszych pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było sześcioro uczniów. Jeśli w każdym przedziale byłoby ośmioro uczniów, to zajęliby oni o 2 przedziały mniej. Ilu uczniów pojechało na tę wycieczkę? Zapisz obliczenia.
Na pozalekcyjne zajęcia sportowe zapisanych jest 37 osób. Uzasadnij, że w tej grupie są co najmniej 4 osoby, które urodziły się w tym samym miesiącu.
Ukryj
Podobne zadania
W pewnym mieście naukę w klasach pierwszych szkół podstawowych rozpoczęło 1854 uczniów urodzonych w roku 2012. Wykaż, że wśród tych uczniów jest co najmniej sześcioro uczniów z taką samą datą urodzenia.
Organizator czterodniowego spływu kajakowego zapłacił za wypożyczenie kajaków 1696 zł. Na koszt wypożyczenia kajaków złożyła się stała dzienna opłata za usługę oraz dodatkowo koszt wypożyczenia każdego z kajaków.
| Opłata stała (niezależna od liczby kajaków) | 64 zł/dzień |
| Każdy z pierwszych 6 kajaków | 35 zł/dzień |
| Każdy kolejny kajak | 30 zł/dzień |
Ile osób wzięło udział w tym spływie, jeżeli w każdym kajaku płynęły dwie osoby?
Gdyby 4 osoby przeszły z partii Cymbałków do partii Trąbek, obie partie liczyłyby tyle samo członków. Gdyby z partii Trąbek 4 osoby przeszły do partii Cymbałków, to w Cymbałkach byłoby 3 razy więcej członków niż w Trąbkach. Ile osób należy do partii Trąbek?
Pociągiem podróżuje 480 osób, przy czym mężczyzn jest o 160 więcej niż kobiet. Ile kobiet podróżuje tym pociągiem?
W zespole tańca nowoczesnego liczba dziewcząt jest dwa razy większa od liczby chłopców. Gdy na próbie nieobecnych było 2 chłopców i 1 dziewczyna, to liczba obecnych chłopców stanowiła 
liczby obecnych dziewcząt. Z ilu osób składa się zespół?
Ukryj
Podobne zadania
Na zawody sportowe miała pojechać grupa uczniów, w której miało być trzy razy więcej chłopców niż dziewcząt. Z powodu choroby na zawody nie pojechało dwóch chłopców i jedna dziewczynka. W konsekwencji, wśród uczniów, którzy pojechali na zawody liczba chłopców była równa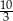 
liczby dziewczynek. Ilu uczniów miało początkowo pojechać na te zawody?
W pewnej szkole 40 uczniów to członkowie SKS-u. Wśród nich 26 gra w siatkówkę, 25 pływa, a 27 jeździ na nartach. Jednocześnie pływa i gra w siatkówkę 15 uczniów, gra w siatkówkę i jeździ na nartach 16, a pływa i jeździ na nartach 18. Jeden uczeń nie zajmuje się sportem. Ilu uczniów uprawia wszystkie trzy dyscypliny sportowe? Ilu uczniów uprawia tylko jedną dyscyplinę sportową?
Uczniów pewnej szkoły ustawiono w kwadrat (tj. tyle samo rzędów, co uczniów w rzędzie). Następnie próbowano ich ustawić w prostokąt, zmniejszając liczbę rzędów o 4, a zwiększając o 5 liczbę uczniów w rzędzie. Okazało się, że brakuje 3 uczniów do wypełnienia tego prostokąta. Ilu uczniów liczyła ta szkoła?
Liczby mieszkańców (w przybliżeniu) Polski, Czech i Słowacji są w stosunku 390:103:54. Różnica liczb mieszkańców w Czechach i Słowacji jest równa 4,9 mln osób. Ilu mieszkańców jest w każdym z tych krajów?
Na wycieczkę wyjechało 38 uczniów. Dzieci spały w 15 pokojach. Dziewczynki spały w pokojach dwuosobowych, a chłopcy spali w pokojach trzyosobowych. Wszystkie miejsca w pokojach były zajęte. Ile dziewczynek i ilu chłopców było na wycieczce? Zapisz obliczenia.
Ukryj
Podobne zadania
Każdy z 240 uczniów pewnej szkoły otrzymał 3 lub 4 darmowe bilety do kina. W sumie rozdano 880 biletów. Ilu uczniów otrzymało 3, a ilu 4 bilety? Zapisz obliczenia.
Uczniowie klasy 3a napisali prace klasową z matematyki. Oceny bardzo dobre otrzymało 30% uczniów, oceny dobre 40% uczniów, oceny dostateczne 8 uczniów, a pozostali uczniowie otrzymali oceny dopuszczające. Średnia ocen z tej klasówki wynosiła 3,9. Ilu uczniów otrzymało poszczególne oceny?
W trzech salach lekcyjnych było początkowo 44 uczniów. Gdy z trzeciej sali 2 uczniów przeszło do pierwszej sali, a z pierwszej sali 6 uczniów przeszło do drugiej sali to okazało się, że w drugiej sali jest dwa razy więcej uczniów niż w pierwszej sali oraz trzy razy więcej uczniów niż w trzeciej sali. Ilu uczniów było początkowo w trzeciej sali?
Powierzchnia Polski wynosi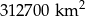 
, a liczba ludności około 38 700 000. Oblicz średnią gęstość zaludnienia w naszym kraju.
Wśród uczestników obozu sportowego było o 28 chłopców więcej niż dziewcząt. W trakcie gry terenowej wszystkich chłopców podzielono na grupy siedmioosobowe, a wszystkie dziewczynki na grupy pięcioosobowe. W ten sposób powstały o 2 więcej grupy składających się z dziewcząt, niż jest grup składających się z chłopców. Ilu chłopców i ile dziewcząt brało udział w tym obozie?
Uczestnicy turnieju szachowego rozgrywali partie według zasady „każdy z każdym”. Uzupełnij tabelę.
| Liczba uczestników turnieju | Liczba wszystkich partii rozegranych przez jednego uczestnika | Liczba wszystkich partii rozegranych w turnieju |
| 2 | 1 | 1 |
| 3 | 2 | 3 |
| 4 | 3 | 6 |
| 5 | 4 | |
| 10 | 45 | |
| 21 | 20 | |
 |  |
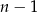Jeżeli uczniów klasy IIb ustawi się trójkami, a uczniów klasy IIc ustawi się parami, to liczba par jest o 3 większa niż liczba trójek. Jeżeli natomiast uczniów klasy IIb ustawi się w parach, a uczniów klasy IIc ustawi się trójkami, to jeden uczeń klasy IIb pozostanie bez pary, a liczba par będzie o 5 większa niż liczba trójek. Ilu uczniów jest w klasach IIb i IIc? Zapisz obliczenia.
Jacek miał wziąć udział w obozie narciarskim, ale zachorował i zamiast niego na obóz pojechał jego dwa razy starszy brat. Ta zamiana spowodowała, że średnia wieku uczestników obozu wzrosła o rok. Oblicz, ile lat ma Jacek, jeżeli w obozie wzięło udział 12 osób. Zapisz obliczenia.
Na statku wycieczkowym są 33 miejsca dla pasażerów. Uczniowie klas IIIa i IIIb planują wycieczkę tym statkiem. W każdej z tych klas jest mniej niż 33 uczniów. Aby wszystkie miejsca dla pasażerów były na statku zajęte, należy do wszystkich uczniów klasy IIIa dołączyć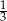 
uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć 
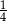uczniów klasy IIIa. Ilu uczniów jest w każdej z tych klas?
Pewna szkoła podstawowa wzięła udział w programie przesiewowych badań słuchu. Pierwszego dnia przebadano 1/5 wszystkich uczniów szkoły. Drugiego dnia przebadano 1/3 pozostałych uczniów. Trzeciego dnia przebadano jeszcze 96 uczniów, a pozostałych 288 uczniów nie wzięło udziału w badaniu. Ilu uczniów uczy się w tej szkole podstawowej?
