Za 4 jednakowe swetry i spodnie zapłacono 384 zł, a za sam sweter i spodnie 132 zł. Ile kosztuje sweter, a ile spodnie?
/Szkoła podstawowa/Zadania z treścią/Ceny i zakupy
Marek kupił w sklepie sportowym kask narciarski, buty i narty. Kask kosztował 500 zł. Narty i kask kosztowały razem o 700 zł mniej niż narty i buty łącznie. Buty i kask kosztowały razem tyle co narty. Oblicz, ile kosztowały narty, a ile kosztowały buty, które kupił Marek w tym sklepie.
Za 4 jednakowe swetry i spodnie zapłacono 464 zł, a za sam sweter i spodnie 242 zł. Ile kosztuje sweter, a ile spodnie?
Cena biletu do teatru jest o 64 zł większa od ceny biletu do kina. Za 4 bilety do teatru i 5 biletów do kina zapłacono łącznie 400 zł. Oblicz cenę jednego biletu do teatru.
Cena biletu do kina jest o 148 zł mniejsza od ceny biletu do teatru. Za 3 bilety do teatru i 5 biletów do kina zapłacono łącznie 700 zł. Oblicz cenę jednego biletu do kina.
Na pływalni w marcu obowiązywała promocja.

Wojtek był w marcu codziennie jeden raz na pływalni i wykorzystał wszystkie ulgi promocyjne. Ile kosztowało go korzystanie z pływalni w marcu?
Pan Stanisław kupił w okolicach Warszawy działkę budowlaną o powierzchni 0,08 ha, płacąc 30 dolarów amerykańskich (USD) za 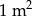 . Przyjmując, że 1 USD=3 zł, oblicz ile pan Stanisław zapłacił za tę działkę.
. Przyjmując, że 1 USD=3 zł, oblicz ile pan Stanisław zapłacił za tę działkę.
Cena godziny korzystania z basenu wynosi 12 zł. Można jednak kupić miesięczną kartę rabatową za 50 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 10 godzin pływania płaci się 8 złotych za godzinę, a za każdą następną godzinę – 9 złotych. Wojtek kupił kartę rabatową i korzystał z basenu przez 16 godzin. Czy zakup karty był dla Wojtka opłacalny? Zapisz obliczenia.
Cena godziny korzystania z kręgielni wynosi 42 zł. Można jednak kupić miesięczną kartę rabatową za 50 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 4 godziny gry płaci się 35 złotych za godzinę, a za każdą następną godzinę – 40 złotych. Ela kupiła kartę rabatową i korzystała z kręgielni przez 12 godzin. Czy zakup karty był dla Eli opłacalny? Zapisz obliczenia.
Cena godziny korzystania z basenu wynosi 12 zł. Można jednak kupić miesięczną kartę rabatową za 49 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 10 godzin pływania płaci się 8 złotych za godzinę, a za każdą następną godzinę – 9 złotych. Kamila kupiła kartę rabatową, a Kacper zdecydował się korzystać z basenu bez karty rabatowej. Po miesiącu korzystania z basenu, okazało się, że Kamila i Kacper byli na basenie przez dokładnie tyle samo godzin, oraz ich wydatki na basen były dokładnie takie same. Ile godzin spędziła na basenie Kamila?
Cena godziny korzystania z basenu wynosi 12 zł. Można jednak kupić miesięczną kartę rabatową za 50 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 10 godzin pływania płaci się 8 złotych za godzinę, a za każdą następną godzinę – 9 złotych. Kamil kupił kartę rabatową i korzystał z basenu przez 15 godzin. Czy zakup karty był dla Kamila opłacalny? Zapisz obliczenia.
Antek stwierdził, że ma tylko 20 zł w skarbonce, a jego kolega Wojtek ma 160 zł. Antek postanowił co tydzień dokładać do skarbonki 2 zł, podczas gdy Wojtek co tydzień wydawał 5 zł ze swych oszczędności. Po ilu tygodniach koledzy będą mieli tyle samo pieniędzy?
Pan Henryk ma do wyboru dwa warianty abonamentu telefonicznego, których szczegóły przedstawiono w poniższej tabeli.
| Wariant I | Wariant II | |
| Miesięczny koszt abonamentu | 30 zł | 24 zł |
| Liczba darmowych minut w abonamencie | 30 | 20 |
| Koszt 1 minuty połączenia | 15 groszy | 20 groszy |
Pan Henryk średnio rozmawia przez telefon przez 90 minut w miesiącu. Który z wariantów abonamentu telefonicznego jest dla niego bardziej korzystny? Zapisz obliczenia.
W tabeli podano wybrane informacje na temat dwóch rodzajów herbat, które pije rodzina Nowaków.
| Rodzaj opakowania | Zawartość opakowania | Cena opakowania | Ilość herbaty potrzebna do zaparzenia jednego kubka naparu |
| herbata w torebkach | 50 torebek | 8,50 zł | 1 torebka |
| herbata sypka | 50 g | 5,00 zł | 2 g |
Rodzina ta wypija dziennie średnio 12 kubków herbaty i zamierza kupić możliwie najmniejszą liczbę opakowań herbaty jednego rodzaju, aby wystarczyło jej na 30 dni. Oblicz koszt zakupu herbaty w torebkach oraz koszt zakupu herbaty sypkiej.
Pani Kowalska pobrała w banku kwotę 1000 zł w banknotach 20 zł i 50 zł. Łącznie otrzymała 32 banknoty. Ile otrzymała banknotów każdego rodzaju?
Na mecz siatkówki wybrała się grupa uczniów z opiekunami, razem 30 osób. Cena biletu normalnego dla opiekuna wynosi 40 zł, a bilet ulgowy dla uczniów jest o 20% tańszy. Łącznie za bilety zapłacono 1016 zł. Oblicz, ilu uczniów i opiekunów udało się na mecz. Zapisz obliczenia.
Piotrek kupił 3 rodzaje ciastek: duże, średnie i małe. Duże ciastko kosztuje 4 zł za sztukę, średnie po 2 zł, a małe po 1 zł. Piotrek kupił łącznie 10 ciastek za które zapłacił 16 zł. Ile kupił dużych ciastek?
Właściciel sklepu sportowego kupił w hurtowni deskorolki i kaski. Cena hurtowa deskorolki była o 60 zł wyższa niż cena hurtowa kasku. Właściciel sklepu ustalił cenę sprzedaży deskorolki o 20% wyższą od ceny hurtowej, a cenę sprzedaży kasku – o 40% wyższą od ceny hurtowej. Deskorolka i kask łącznie kosztowały w sklepie 397 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej deskorolki i jednego kasku. Zapisz obliczenia.
Właściciel sklepu komputerowego kupił w hurtowni klawiatury i myszki. Cena hurtowa klawiatury była o 30 zł wyższa niż cena hurtowa myszki. Właściciel sklepu ustalił cenę sprzedaży klawiatury o 10% wyższą od ceny hurtowej, a cenę sprzedaży myszki – o 30% wyższą od ceny hurtowej. Klawiatura i myszka łącznie kosztowały w sklepie 213 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej klawiatury i jednej myszki. Zapisz obliczenia.
Ania chciała kupić 10 jednakowych puszek karmy dla psa, ale zabrakło jej 11 złotych. Kupiła 6 takich puszek karmy i zostało jej 3,40 złotych. Ile kosztuje jedna puszka karmy?
Adrian chciał kupić 12 jednakowych butelek soku owocowego, ale zabrakło mu 23,80 złotych. Kupił więc 8 butelek soku i zostało mu 5,80 złotego. Ile kosztuje jedna butelka tego soku?
Do sklepu warzywno-owocowego zakupiono w hurtowni 250 kg pomidorów za 800 zł. Pierwszego dnia sprzedano 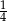 ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia
ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia 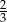 tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
Maja, Ola i Jagna kupowały zeszyty. Maja za 3 grube zeszyty i 8 cienkich zapłaciła 10 zł. Ola kupiła 4 grube oraz 4 cienkie zeszyty i również zapłaciła 10 zł. Czy Jagnie wystarczy 10 złotych na zakup 5 grubych zeszytów i 1 cienkiego? Zapisz obliczenia i odpowiedź.
Olaf, Kacper i Łukasz kupowali słodycze. Olaf za 10 cukierków czekoladowych i 3 lizaki zapłacił 21 zł. Kacper kupił 6 cukierków czekoladowych i 6 lizaków i również zapłacił 21 zł. Czy Łukaszowi wystarczy 21 złotych na zakup 8 cukierków czekoladowych i 4 lizaków? Zapisz obliczenia i odpowiedź.
Troje przyjaciół: Adam, Wojtek i Karol postanowiło kupić losy na loterii, w której jeden los kosztował 4 zł. Adam kupił 12 losów, Wojtek kupił 9 losów, a Karol kupił 3 losy. Po sprawdzeniu wszystkich losów okazało się, że chłopcy wygrali w sumie 168 zł. Wygraną kwotę postanowili podzielić następująco: każdy z chłopców z wygranej kwoty zabrał tyle pieniędzy, ile wydał na losy, a pozostałą kwotę chłopcy podzieli między siebie, proporcjonalnie do liczby kupionych losów. Ile pieniędzy z wygranych 168 zł otrzymał każdy z chłopców?
Na zakup biletów do kina klasa 3a zebrała 360 zł, klasy 3b i 3c po 300 zł, a klasa 3d – 240 zł. Szkole udzielono rabatu i wszystkie bilety kosztowały 1000 zł. Uzyskany rabat podzielono między cztery klasy proporcjonalnie do zebranych kwot. Jaką kwotę zwrócono klasie 3a?
Trzy sąsiadki zamówiły wspólnie kawę w sklepie internetowym. Kawa dla pani Malinowskiej miała kosztować 120 zł, a dla pani Wiśniewskiej i dla pani Śliwińskiej – po 90 zł. Sąsiadki przy zakupie otrzymały rabat i za zamówioną kawę zapłaciły 260 zł. Oblicz, ile pieniędzy powinna zapłacić każda z pań, aby jej wpłata była proporcjonalna do pierwotnej wartości zamówienia.
Jacek, Marek, Karol i Andrzej kupili losy na loterii, przy czym Jacek kupił losy za 24 zł, Marek kupił losy za 36 zł, a Karol i Andrzej kupili losy za 30 złoty każdy. Wśród kupionych losów jeden okazał się być wygrywającym i chłopcy otrzymali 600 zł nagrody. Otrzymaną kwotę chłopcy podzielili następująco: każdy otrzymał zwrot kosztów zakupu losów, a pozostałą kwotę podzieli pomiędzy siebie proporcjonalnie do kwot, które przeznaczyli na zakup losów. Ile pieniędzy z nagrody (nie licząc zwrotu kosztów zakupu losów) otrzymał Marek?
W tabeli podano cenniki dwóch korporacji taksówkowych. Należność za przejazd składa się z jednorazowej opłaty początkowej i doliczonej do niej opłaty zależnej od długości przejechanej trasy.
| Taxi „Jedynka” | Taxi „Dwójka” | |
| Opłata początkowa | 3,20 zł | 8,00 zł |
| Cena za 1 km trasy | 3,20 zł | 2,40 zł |
Pan Jan korzystał z Taxi „Jedynka”, a pan Wojciech – z Taxi „Dwójka”. Obaj panowie pokonali trasę o tej samej długości i zapłacili tyle samo. Ile kilometrów miała trasa, którą przejechał każdy z nich?
Pewną kwotę rozdzielono na trzy nagrody pieniężne. Marcin dostał 2 razy więcej pieniędzy niż Jędrek, a Kamil 2 razy mniej niż Jędrek. Uzasadnij, że Kamil otrzymał 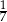 tej kwoty.
tej kwoty.
Pewną liczbę cukierków rozdzielono pomiędzy trzy osoby. Kasia otrzymała 3 razy mniej cukierków niż Zosia, a Ela 2 razy więcej niż Zosia. Uzasadnij, że Kasia otrzymała 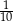 wszystkich cukierków.
wszystkich cukierków.
Na przedstawienie sprzedano 200 biletów po 25 zł i 35 zł. Po potrąceniu 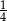 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4650 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4650 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
Na przedstawienie sprzedano 300 biletów po 15 zł i 20 zł. Po potrąceniu 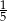 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
W wypożyczalni Gierka za wypożyczenie gry planszowej trzeba zapłacić 8 zł za 3 dni i dodatkowo po 2,50 zł za każdy kolejny dzień wypożyczenia. Natomiast w wypożyczalni Planszówka płaci się 12 zł za 3 dni i po 2 zł za każdy kolejny dzień. Przy jakiej liczbie dni koszty wypożyczenia tej gry w jednej i drugiej wypożyczalni są jednakowe?
Lodziarnia sprzedaje małe lody po 1,50 zł, a duże po 2,5 zł. Pewnego dnia sprzedano 190 lodów, otrzymując ze sprzedaży 415 zł. Ile dużych i ile małych lodów sprzedano?

