Rozwiązaniem równania 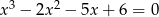 nie jest liczba
nie jest liczba
A) 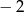 B) 1 C) 4 D) 3
B) 1 C) 4 D) 3
/Szkoła średnia/Zadania testowe/Równania/Wielomianowe/Stopnia 3
Suma wszystkich pierwiastków równania 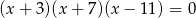 jest równa
jest równa
A) 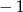 B) 21 C) 1 D)
B) 21 C) 1 D) 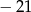
Suma wszystkich rozwiązań równania 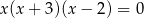 jest równa
jest równa
A) 0 B) 1 C) 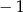 D) 6
D) 6
Suma wszystkich rozwiązań równania 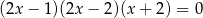 jest równa
jest równa
A) 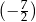 B)
B) 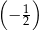 C)
C) 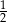 D) 1
D) 1
Suma wszystkich rozwiązań równania 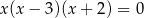 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Iloczyn wszystkich pierwiastków równania 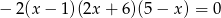 jest równy
jest równy
A) 15 B) 30 C) 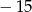 D)
D) 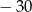
Suma wszystkich pierwiastków równania 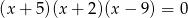 jest równa
jest równa
A) 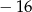 B) 2 C) 16 D)
B) 2 C) 16 D) 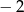
Jednym z rozwiązań równania 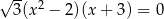 jest liczba
jest liczba
A) 3 B) 2 C) 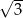 D)
D) 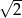
Jednym z rozwiązań równania 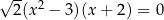 jest liczba
jest liczba
A) 3 B) 2 C) 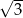 D)
D) 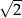
Suma odwrotności pierwiastków wielomianu 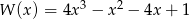 jest równa
jest równa
A) 4 B) 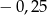 C) 6 D)
C) 6 D) 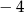
Równanie 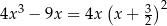 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
Wśród miejsc zerowych wielomianu są liczby 0, 1, 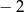 . Wielomian może mieć postać:
. Wielomian może mieć postać:
A) 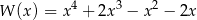 B)
B) 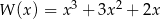
C) 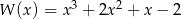 D)
D) 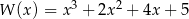
Liczba niewymiernych pierwiastków równania 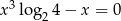 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba niewymiernych pierwiastków równania 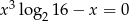 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba niewymiernych pierwiastków równania 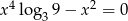 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba pierwiastków wielomianu 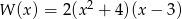 jest równa
jest równa
A) 4 B) 3 C) 2 D) 1
Liczba pierwiastków rzeczywistych wielomianu 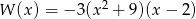 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba rozwiązań równania 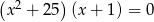 to
to
A) 3 B) 2 C) 1 D) 0
Dany jest wielomian 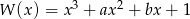 , gdzie
, gdzie  i
i 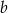 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Równanie 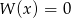 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
B) Jeżeli równanie 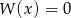 ma pierwiastek całkowity, to
ma pierwiastek całkowity, to 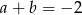 .
.
C) Jeżeli równanie 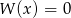 ma ujemny pierwiastek wymierny, to
ma ujemny pierwiastek wymierny, to 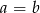 .
.
D) Równanie 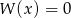 może nie mieć rozwiązań.
może nie mieć rozwiązań.
Dany jest wielomian 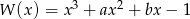 , gdzie
, gdzie  i
i 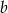 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 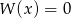 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 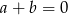 .
.
B) Jeżeli równanie 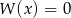 ma ujemny pierwiastek całkowity, to
ma ujemny pierwiastek całkowity, to 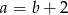 .
.
C) Równanie 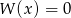 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 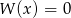 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Dany jest wielomian 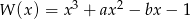 , gdzie
, gdzie  i
i 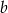 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 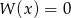 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 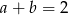 .
.
B) Jeżeli równanie 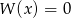 ma dodatni pierwiastek całkowity, to
ma dodatni pierwiastek całkowity, to 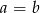 .
.
C) Równanie 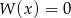 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 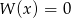 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Liczba 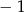 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 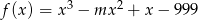 . Zatem
. Zatem
A) 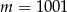 B)
B) 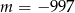 C)
C) 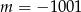 D)
D) 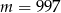
Liczba 5 jest pierwiastkiem wielomianu 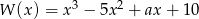 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 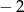 B)
B) 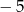 C) 2 D) 5
C) 2 D) 5
Liczba 2 jest pierwiastkiem wielomianu 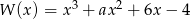 . Współczynnik
. Współczynnik  jest równy
jest równy
A) 2 B) -2 C) 4 D) -4
Liczba 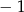 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 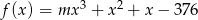 . Zatem
. Zatem
A) 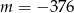 B)
B) 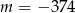 C)
C) 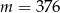 D)
D) 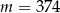
Liczby 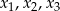 są rozwiązaniami równania
są rozwiązaniami równania 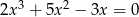 . Suma
. Suma 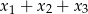 jest równa
jest równa
A) 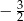 B)
B) 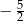 C)
C) 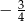 D)
D) 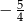
Zbiorem wszystkich rozwiązań równania 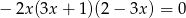 jest
jest
A) 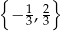 B)
B) 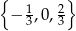 C)
C) 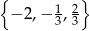 D)
D) 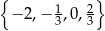
Funkcja 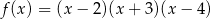 ma
ma
A) 1 miejsce zerowe B) 2 miejsca zerowe
C) 3 miejsca zerowe D) nie ma miejsc zerowych
Funkcja 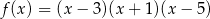
A) nie ma miejsc zerowych B) ma 1 miejsce zerowe
C) ma 2 miejsca zerowe D) ma 3 miejsca zerowe
Iloczyn wszystkich rozwiązań równania 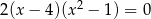 jest równy
jest równy
A) 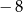 B)
B) 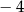 C) 4 D) 8
C) 4 D) 8
Iloczyn wszystkich rozwiązań równania 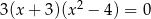 jest równy
jest równy
A) 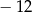 B)
B) 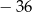 C) 36 D) 12
C) 36 D) 12
Równanie 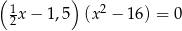
A) ma trzy różne rozwiązania B) ma dwa różne rozwiązania
C) ma jedno rozwiązanie D) nie ma rozwiązań
Liczba pierwiastków wielomianu 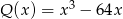 , które są liczbami parzystymi jest równa
, które są liczbami parzystymi jest równa
A) 0 B) 1 C) 2 D) 3
Liczba pierwiastków wielomianu 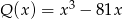 , które są liczbami parzystymi jest równa
, które są liczbami parzystymi jest równa
A) 0 B) 1 C) 2 D) 3
Rozwiązaniem równania 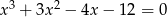 nie jest liczba
nie jest liczba
A) 2 B) 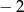 C)
C) 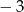 D) 3
D) 3
Dany jest wielomian 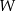 określony wzorem
określony wzorem 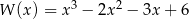 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 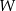 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 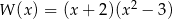 B)
B) 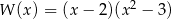
C) 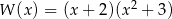 D)
D) 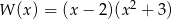
Dany jest wielomian 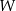 określony wzorem
określony wzorem 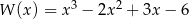 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 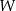 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 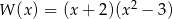 B)
B) 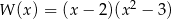
C) 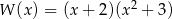 D)
D) 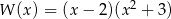
Pierwiastkami równania 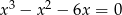 są liczby
są liczby
A) 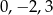 B)
B) 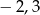 C)
C) 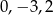 D)
D) 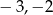
Iloczyn pierwiastków równania 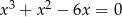 jest równy
jest równy
A) 1 B) 3 C) 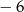 D) 0
D) 0

