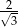Obwód trójkąta równobocznego jest równy 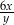 , gdzie
, gdzie 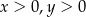 . Pole powierzchni tego trójkąta jest równe
. Pole powierzchni tego trójkąta jest równe
A) 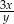 B)
B) 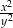 C)
C) 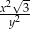 D)
D) 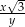
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Równoboczny
Okrąg wpisany w trójkąt równoboczny ma promień równy 6. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 36 D) 24
Okrąg wpisany w trójkąt równoboczny ma promień równy 8. Wysokość tego trójkąta jest równa
A) 12 B) 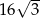 C)
C) 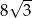 D) 24
D) 24
Długość boku trójkąta równobocznego wynosi 8. Pole koła opisanego na tym trójkącie jest równe
A) 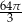 B)
B) 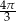 C)
C) 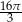 D)
D) 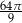
Wysokość trójkąta równobocznego jest o 2 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 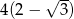 B)
B) 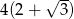 C)
C) 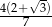 D)
D) 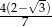
Wysokość trójkąta równobocznego jest o 3 krótsza od boku tego trójkąta. Bok trójkąta jest ma długość
A) 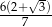 B)
B) 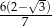 C)
C) 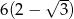 D)
D) 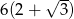
Wysokość trójkąta równobocznego jest o 4 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 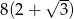 B)
B) 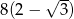 C)
C) 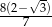 D)
D) 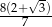
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 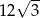 B)
B) 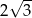 C)
C)  D)
D) 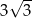
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 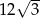 B)
B) 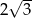 C)
C) 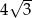 D)
D) 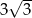
Promień okręgu wpisanego w trójkąt równoboczny jest o 1 krótszy od promienia okręgu opisanego na tym trójkącie. Bok trójkąta ma więc długość
A) 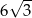 B)
B) 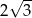 C)
C) 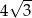 D)
D) 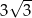
Długość boku trójkąta równobocznego wynosi 12. Pole koła wpisanego w ten trójkąt jest równe
A) 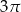 B)
B) 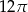 C)
C) 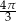 D)
D) 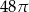
Dany jest trójkąt równoboczny, którego pole jest równe 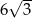 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 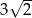 B)
B) 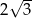 C)
C) 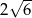 D)
D) 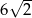
Pole pewnego trójkąta równobocznego jest równe 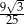 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 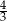 D)
D) 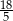
Dany jest trójkąt równoboczny, którego pole jest równe 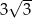 . Bok tego trójkąta ma długość
. Bok tego trójkąta ma długość
A) 3 B) 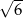 C) 6 D)
C) 6 D) 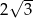
Pole pewnego trójkąta równobocznego jest równe 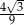 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 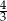 D)
D) 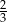
Pole trójkąta równobocznego o obwodzie 6 jest równe
A) 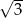 B)
B) 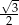 C)
C) 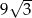 D)
D) 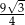
W trójkącie równobocznym 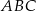 poprowadzono odcinki
poprowadzono odcinki 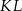 i
i 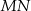 , które podzieliły boki
, które podzieliły boki 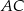 i
i 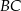 na trzy równe części. Stosunek pola trójkąta
na trzy równe części. Stosunek pola trójkąta 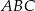 do pola trapezu
do pola trapezu 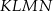 jest równy
jest równy
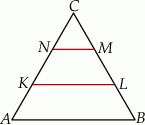
A) 3 B) 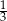 C) 9 D) 6
C) 9 D) 6
Okrąg opisany na trójkącie równobocznym ma promień równy 6. Wysokość tego trójkąta jest równa
A) 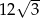 B) 18 C) 9 D)
B) 18 C) 9 D) 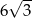
Okrąg opisany na trójkącie równobocznym ma promień równy 8. Wysokość tego trójkąta jest równa
A) 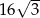 B) 12 C) 24 D)
B) 12 C) 24 D) 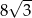
Promień okręgu opisanego na trójkącie równobocznym jest równy 8. Wysokość tego trójkąta jest równa
A) 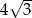 B)
B) 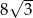 C) 12 D) 6
C) 12 D) 6
Okrąg opisany na trójkącie równobocznym ma promień równy 12. Wysokość tego trójkąta jest równa
A) 18 B) 20 C) 22 D) 24
Pole trójkąta równobocznego 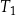 jest równe
jest równe 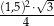 . Pole trójkąta równobocznego
. Pole trójkąta równobocznego 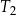 jest równe
jest równe 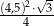 . Trójkąt
. Trójkąt 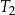 jest podobny do trójkąta
jest podobny do trójkąta 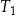 w skali
w skali
| A) 3, | B) 9, |
ponieważ
| 1) | każdy z tych trójkątów ma dokładnie trzy osie symetrii. |
| 2) | pole trójkąta 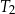 jest 9 razy większe od pola trójkąta jest 9 razy większe od pola trójkąta 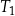 . . |
| 3) | bok trójkąta 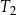 jest o 3 dłuższy od boku trójkąta jest o 3 dłuższy od boku trójkąta 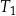 . . |
Pole trójkąta równobocznego 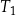 jest równe
jest równe 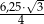 . Pole trójkąta równobocznego
. Pole trójkąta równobocznego 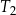 jest równe
jest równe 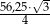 . Trójkąt
. Trójkąt 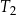 jest podobny do trójkąta
jest podobny do trójkąta 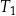 w skali
w skali
| A) 5, | B) 3, |
ponieważ
| 1) | pole trójkąta 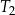 jest 25 razy większe od pola trójkąta jest 25 razy większe od pola trójkąta 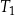 . . |
| 2) | bok trójkąta 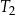 jest o 5 dłuższy od boku trójkąta jest o 5 dłuższy od boku trójkąta 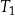 . . |
| 3) | bok trójkąta 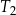 jest 3 razy dłuższy od boku trójkąta jest 3 razy dłuższy od boku trójkąta 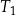 . . |
Wysokość trójkąta równobocznego 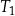 jest równa
jest równa 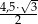 . Wysokość trójkąta równobocznego
. Wysokość trójkąta równobocznego 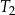 jest równa
jest równa 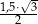 . Stosunek pola trójkąta
. Stosunek pola trójkąta 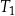 do pola trójkąta
do pola trójkąta 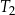 jest równy
jest równy
| A) 3, | B) 9, |
ponieważ
| 1) | bok trójkąta 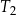 jest 9 razy krótszy od boku trójkąta jest 9 razy krótszy od boku trójkąta 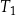 . . |
| 2) | wysokość trójkąta 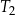 jest 3 razy krótsza od wysokości trójkąta jest 3 razy krótsza od wysokości trójkąta 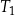 . . |
| 3) | bok trójkąta 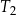 jest o 3 krótszy od boku trójkąta jest o 3 krótszy od boku trójkąta 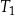 . . |
Promień okręgu wpisanego w trójkąt równoboczny jest o 2 krótszy od promienia okręgu opisanego na tym trójkącie. Wysokość trójkąta ma więc długość
A) 6 B) 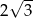 C)
C) 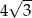 D) 12
D) 12
Promień okręgu wpisanego w trójkąt równoboczny jest o 3 krótszy od promienia okręgu opisanego na tym trójkącie. Wysokość trójkąta ma więc długość
A) 6 B) 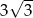 C)
C) 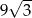 D) 9
D) 9
Symetralne boków trójkąta równobocznego przecinają się w punkcie odległym od wierzchołka o 5 cm. Wysokość tego trójkąta ma długość
A) 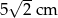 B)
B) 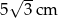 C)
C) 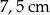 D)
D) 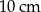
Symetralne boków trójkąta równobocznego przecinają się w punkcie odległym od boku trójkąta o 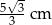 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 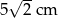 B)
B) 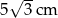 C)
C) 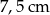 D)
D) 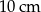
Jeżeli wysokość trójkąta równobocznego wynosi 2, to długość jego boku jest równa
A) 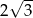 B)
B) 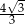 C)
C) 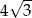 D) 6
D) 6
Długość boku trójkąta równobocznego o wysokości 6 cm jest równa:
A) 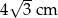 B) 12 cm C)
B) 12 cm C) 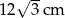 D)
D) 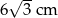
Jeżeli wysokość trójkąta równobocznego wynosi 4, to długość jego boku jest równa
A) 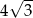 B)
B) 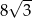 C)
C) 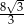 D) 12
D) 12
Jeżeli wysokość trójkąta równobocznego wynosi 6, to długość jego boku jest równa
A) 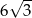 B)
B) 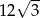 C)
C) 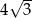 D) 18
D) 18
Jeżeli wysokość trójkąta równobocznego wynosi 3, to długość jego boku jest równa
A) 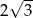 B)
B) 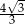 C)
C) 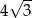 D) 6
D) 6
W trójkącie równobocznym wysokość jest równa 12. Zatem bok tego trójkąta ma długość
A) 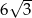 B)
B) 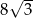 C) 24 D) 8
C) 24 D) 8
Długość boku trójkąta równobocznego jest równa 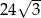 . Promień okręgu wpisanego w ten trójkąt jest równy
. Promień okręgu wpisanego w ten trójkąt jest równy
A) 36 B) 18 C) 12 D) 6
Długość boku trójkąta równobocznego jest równa 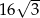 . Promień okręgu wpisanego w ten trójkąt jest równy
. Promień okręgu wpisanego w ten trójkąt jest równy
A) 4 B) 8 C) 12 D) 24
W trójkącie równobocznym długość każdego boku zmniejszono o 20%. Wtedy pole tego trójkąta
A) zmniejszy się o 20% B) zmniejszy się o 40%
C) zmniejszy się o mniej niż 20% D) zmniejszy się o 36%
Pole trójkąta równobocznego wpisanego w koło o polu 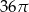 jest równe
jest równe
A) 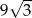 B) 81 C)
B) 81 C) 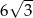 D)
D) 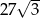
Wysokość trójkąta równobocznego o długości boku 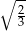 wynosi
wynosi
A) 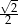 B)
B) 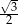 C)
C) 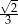 D)
D) 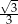
Pole koła opisanego na trójkącie równobocznym jest równe 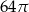 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 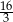 B) 16 C) 12 D) 24
B) 16 C) 12 D) 24
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku kwadratu do długości boku trójkąta równobocznego jest wtedy równy
A) 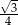 B)
B) 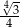 C)
C) 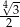 D)
D) 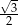
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku trójkąta równobocznego do długości boku kwadratu jest wtedy równy
A) 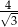 B)
B) 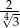 C)
C) 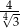 D)
D)