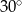Czworokąty 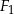 i
i 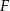 są podobne. Pole czworokąta
są podobne. Pole czworokąta 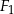 jest o 36% mniejsze od pola czworokąta
jest o 36% mniejsze od pola czworokąta 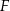 . Obwód czworokąta
. Obwód czworokąta 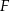 jest większy od obwodu czworokąta
jest większy od obwodu czworokąta 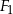 o:
o:
A) 20% B) 25% C) 36% D) 18%
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt/Dowolny
Czworokąt 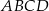 jest deltoidem (zobacz rysunek), w którym
jest deltoidem (zobacz rysunek), w którym 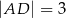 ,
, 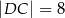 oraz
oraz 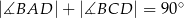 .
.
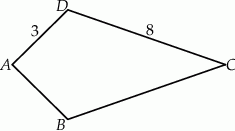
Pole tego deltoidu jest równe
A) 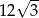 B)
B) 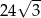 C)
C) 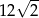 D)
D) 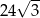
Czworokąt 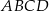 jest wpisany w okrąg, przy czym przekątna
jest wpisany w okrąg, przy czym przekątna 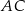 jest średnicą tego okręgu oraz
jest średnicą tego okręgu oraz 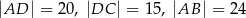 . Wtedy
. Wtedy
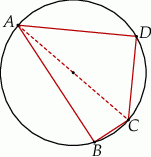
A) 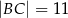 B)
B) 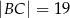 C)
C) 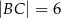 D)
D) 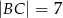
Który z czworokątów ma zawsze więcej niż dwie osie symetrii?
A) deltoid B) prostokąt C) kwadrat D) romb
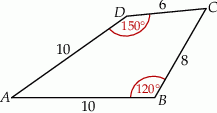
Pole czworokąta przedstawionego na rysunku jest równe
A) 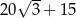 B)
B) 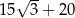 C)
C) 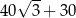 D)
D) 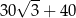
Czworokąt 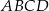 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 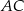 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 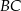 i
i 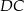 , a kąt
, a kąt 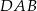 ma miarę
ma miarę 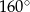 .
.
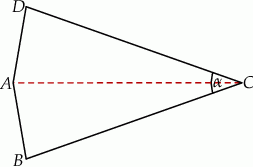
Miara kąta 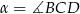 jest równa
jest równa
A) 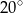 B)
B) 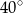 C)
C) 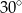 D)
D) 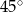
Punkty 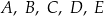 leżą na okręgu o środku
leżą na okręgu o środku 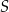 . Miara kąta
. Miara kąta 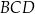 jest równa
jest równa 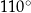 , a miara kąta
, a miara kąta 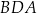 jest równa
jest równa 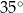 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 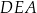 ma miarę równą
ma miarę równą
A) 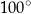 B)
B) 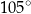 C)
C) 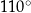 D)
D) 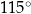
Odległości punktu 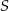 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 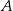 i
i 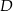 są równe
są równe 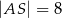 i
i 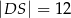 . Bok
. Bok 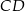 tego czworokąta ma długość
tego czworokąta ma długość
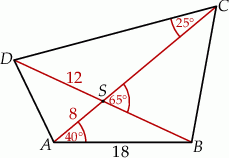
A) 27 B) 16 C) 24 D) 30
Które z poniższych zdań nie jest prawdziwe?
A) Na każdym prostokącie można opisać okrąg.
B) W każdy romb można wpisać okrąg.
C) Na każdym równoległoboku można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Które z poniższych zdań nie jest prawdziwe?
A) W każdy romb można wpisać okrąg.
B) W każdy prostokąt można wpisać okrąg.
C) Na każdym prostokącie można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Różnica miar dwóch przeciwległych kątów deltoidu jest równa 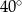 . Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
. Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
A) 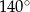 B)
B) 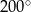 C)
C) 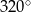 D)
D) 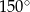
Na czworokącie 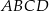 opisano okrąg o środku
opisano okrąg o środku 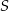 i promieniu
i promieniu 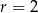 (zobacz rysunek). Pole tego czworokąta jest równe
(zobacz rysunek). Pole tego czworokąta jest równe
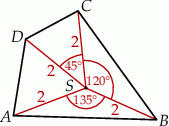
A) 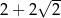 B) 4 C)
B) 4 C) 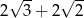 D)
D) 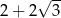
Przekątna 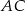 jest średnicą okręgu opisanego na czworokącie
jest średnicą okręgu opisanego na czworokącie 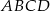 . Punkt przecięcia przekątnych dzieli przekątną
. Punkt przecięcia przekątnych dzieli przekątną 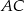 na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie
na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie 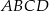 jest równa
jest równa
A) 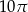 B)
B) 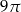 C)
C) 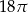 D)
D) 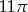
Pole czworokąta 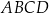 jest równe
jest równe 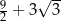 . Ponadto:
. Ponadto: 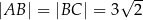 ,
, 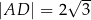 ,
, 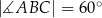 ,
, 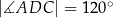 (zobacz rysunek).
(zobacz rysunek).
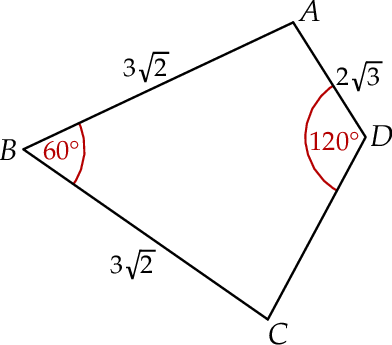
Długość boku 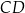 jest równa
jest równa
A) 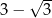 B)
B) 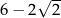 C)
C) 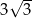 D)
D) 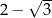
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 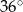 B)
B) 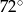 C)
C) 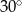 D)
D) 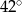
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem największy kąt tego wielokąta ma miarę
A) 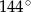 B)
B) 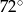 C)
C) 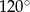 D)
D) 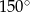
Stosunek miar kątów czworokąta jest równy 6:7:8:9. Najmniejszy kąt tego czworokąta ma miarę
A) 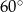 B)
B) 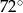 C)
C) 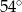 D)
D) 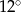
Miary kątów pewnego czworokąta pozostają w stosunku 2:3:3:4. Wynika stąd, że najmniejszy kąt tego czworokąta ma miarę
A) 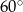 B)
B) 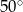 C)
C) 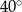 D)
D)