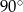W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
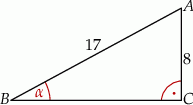
A) 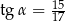 B)
B) 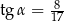 C)
C) 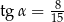 D)
D) 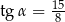
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy

A) 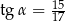 B)
B) 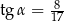 C)
C) 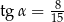 D)
D) 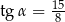
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
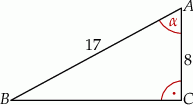
A) 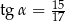 B)
B) 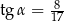 C)
C) 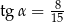 D)
D) 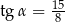
W trójkącie prostokątnym (patrz rysunek poniżej) tangens kąta ostrego  jest równy
jest równy
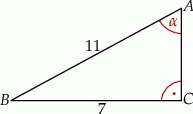
A) 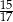 B)
B) 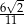 C)
C) 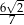 D)
D) 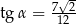
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
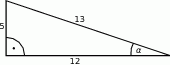
A) 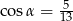 B)
B) 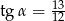 C)
C) 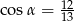 D)
D) 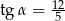
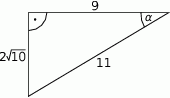
W trójkącie prostokątnym dane są długości boków (zobacz rysunek). Wtedy
A) 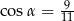 B)
B) 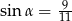 C)
C) 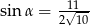 D)
D) 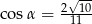
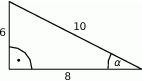
Na rysunku zaznaczono długości boków i kąt  trójkąta prostokątnego (zobacz rysunek). Wtedy
trójkąta prostokątnego (zobacz rysunek). Wtedy
A) 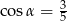 B)
B) 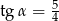 C)
C) 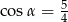 D)
D) 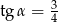
Dany jest trójkąt prostokątny (patrz rysunek).
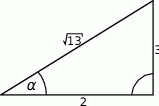
Wartość wyrażenia 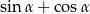 wynosi
wynosi
A) 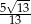 B)
B) 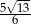 C)
C) 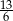 D) 1
D) 1
Dany jest trójkąt prostokątny (patrz rysunek).
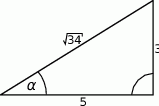
Wartość wyrażenia 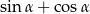 wynosi
wynosi
A) 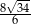 B)
B) 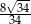 C)
C) 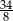 D) 1
D) 1
Dany jest trójkąt prostokątny (patrz rysunek).
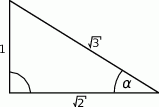
Wtedy 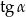 jest równy
jest równy
A) 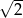 B)
B) 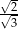 C)
C) 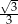 D)
D) 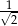
Dany jest trójkąt prostokątny (patrz rysunek).
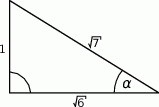
Wtedy 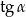 jest równy
jest równy
A) 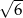 B)
B) 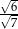 C)
C) 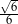 D)
D) 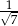
Dany jest trójkąt prostokątny (patrz rysunek).
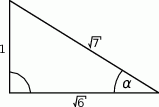
Wtedy 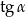 jest równy
jest równy
A) 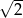 B)
B) 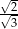 C)
C) 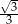 D)
D) 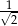
Dany jest trójkąt prostokątny (patrz rysunek).
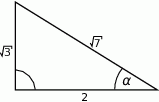
Wtedy 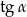 jest równy
jest równy
A) 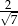 B)
B) 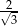 C)
C) 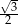 D)
D) 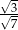
Przeciwprostokątna 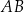 trójkąta prostokątnego
trójkąta prostokątnego 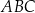 ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
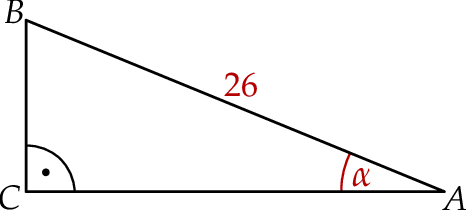
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 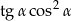 jest równa
jest równa
A) 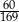 B)
B) 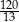 C)
C) 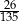 D)
D) 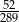
Dany jest trójkąt prostokątny o kątach ostrych  i
i 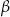 (zobacz rysunek).
(zobacz rysunek).
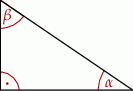
Wyrażenie 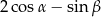 jest równe
jest równe
A) 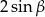 B)
B) 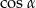 C) 0 D) 2
C) 0 D) 2
Dany jest trójkąt prostokątny o kątach ostrych  i
i 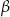 (zobacz rysunek).
(zobacz rysunek).
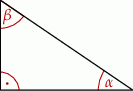
Wyrażenie 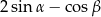 jest równe
jest równe
A) 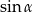 B)
B) 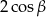 C) 0 D) 2
C) 0 D) 2
Dane są długości boków 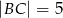 i
i 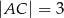 trójkąta prostokątnego
trójkąta prostokątnego 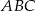 o kącie ostrym
o kącie ostrym 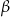 (zobacz rysunek).
(zobacz rysunek).
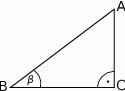
Wtedy
A) 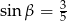 B)
B) 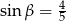 C)
C) 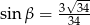 D)
D) 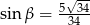
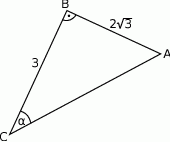
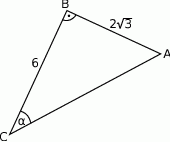
W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego  jest równy
jest równy
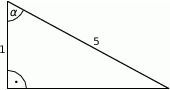
A) 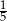 B)
B) 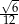 C)
C) 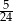 D)
D) 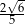
Dane są długości boków 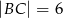 i
i 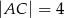 trójkąta prostokątnego
trójkąta prostokątnego 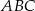 o kącie ostrym
o kącie ostrym 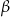 (zobacz rysunek).
(zobacz rysunek).
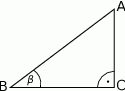
Wtedy
A) 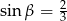 B)
B) 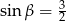 C)
C) 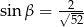 D)
D) 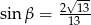
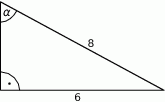
W trójkącie, przedstawionym na rysunku poniżej, cosinus kąta ostrego  jest równy
jest równy
A)  B)
B)  C)
C) 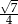 D)
D) 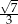
W trójkącie prostokątnym 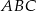 przyprostokątne mają długość
przyprostokątne mają długość 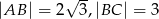 , a kąt
, a kąt 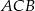 ma miarę
ma miarę  .
.
Zatem
A) 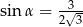 B)
B) 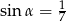 C)
C) 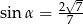 D)
D) 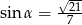
W trójkącie prostokątnym 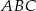 przyprostokątne mają długość
przyprostokątne mają długość 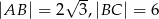 , a kąt
, a kąt 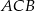 ma miarę
ma miarę  .
.
Zatem
A) 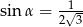 B)
B) 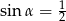 C)
C) 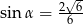 D)
D) 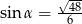
W trójkącie prostokątnym 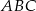 przyprostokątne mają długość
przyprostokątne mają długość 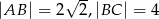 , a kąt
, a kąt 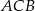 ma miarę
ma miarę  .
.
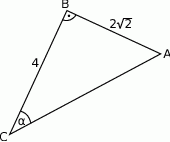
Zatem
A) 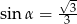 B)
B) 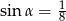 C)
C) 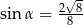 D)
D) 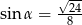
Dany jest trójkąt prostokątny (patrz rysunek).
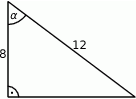
Wartość wyrażenia 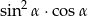 wynosi
wynosi
A) 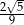 B)
B)  C)
C) 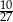 D)
D) 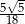
Odcinek 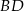 jest zawarty w dwusiecznej kąta ostrego
jest zawarty w dwusiecznej kąta ostrego 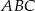 trójkąta prostokątnego, w którym przyprostokątne
trójkąta prostokątnego, w którym przyprostokątne 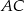 i
i 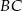 mają długości odpowiednio 5 i 3.
mają długości odpowiednio 5 i 3.
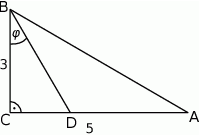
Wówczas miara 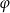 kąta
kąta 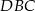 spełnia warunek
spełnia warunek
A) 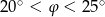 B)
B) 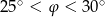 C)
C) 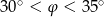 D)
D) 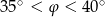
Odcinek 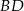 jest zawarty w dwusiecznej kąta ostrego
jest zawarty w dwusiecznej kąta ostrego 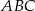 trójkąta prostokątnego, w którym przyprostokątne
trójkąta prostokątnego, w którym przyprostokątne 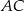 i
i 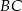 mają długości odpowiednio 8 i 3.
mają długości odpowiednio 8 i 3.
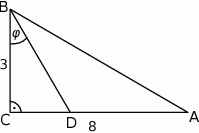
Wówczas miara 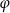 kąta
kąta 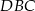 spełnia warunek
spełnia warunek
A) 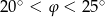 B)
B) 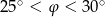 C)
C) 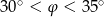 D)
D) 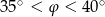
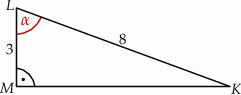
Przyprostokątna 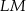 trójkąta prostokątnego
trójkąta prostokątnego 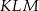 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 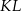 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
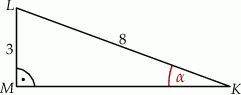
Wtedy miara  kąta ostrego
kąta ostrego 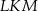 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 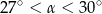 B)
B) 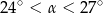 C)
C) 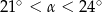 D)
D) 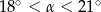
Przyprostokątna 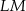 trójkąta prostokątnego
trójkąta prostokątnego 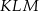 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 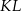 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
Wtedy miara  kąta ostrego
kąta ostrego 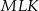 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 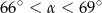 B)
B) 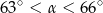 C)
C) 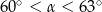 D)
D) 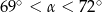
W trójkącie prostokątnym 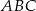 , w którym
, w którym 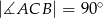 , na boku
, na boku 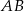 wybrano punkt
wybrano punkt 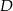 taki, że
taki, że 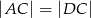 (zobacz rysunek).
(zobacz rysunek).
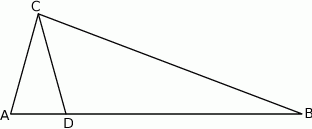
Wynika stąd, że różnica miar kątów 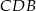 i
i 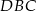 jest równa
jest równa
A) 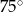 B)
B) 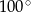 C)
C) 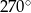 D)
D)