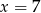Rozwiązaniem układu równań 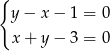 jest para
jest para
A) 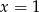 i
i 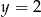 B)
B) 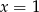 i
i 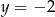 C)
C) 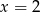 i
i 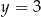 D)
D) 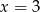 i
i 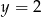
/Szkoła podstawowa/Zadania testowe/Układy równań
Rozwiązaniem układu równań 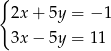 jest
jest
A) 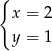 B)
B) 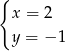 C)
C) 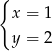 D)
D) 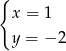
Rozwiązaniem układu równań 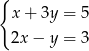 jest
jest
A) 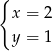 B)
B) 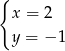 C)
C) 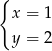 D)
D) 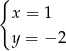
Rozwiązaniem układu równań 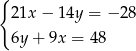 jest para liczb
jest para liczb
A) 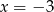 i
i 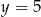 B)
B) 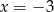 i
i 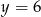 C)
C) 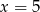 i
i 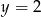 D)
D) 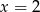 i
i 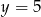
Dany jest układ równań
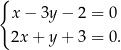
Rozwiązaniem tego układu równań jest para liczb
A) 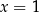 i
i 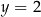 B)
B) 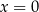 i
i 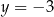 C)
C) 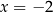 i
i 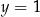 D)
D) 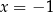 i
i 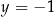
Dany jest układ równań
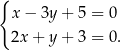
Rozwiązaniem tego układu równań jest para liczb
A) 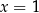 i
i 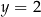 B)
B) 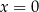 i
i 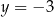 C)
C) 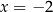 i
i 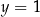 D)
D) 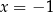 i
i 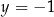
Układ równań 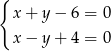 opisuje w układzie współrzędnych na płaszczyźnie punkt
opisuje w układzie współrzędnych na płaszczyźnie punkt
A) 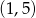 B)
B) 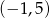 C)
C) 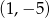 D)
D) 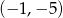
Rozwiązaniem układu równań 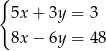 jest para liczb
jest para liczb
A) 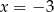 i
i 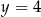 B)
B) 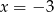 i
i 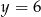 C)
C) 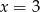 i
i 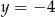 D)
D) 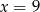 i
i 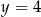
Rozwiązaniem układu równań 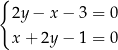 jest para
jest para
A) 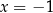 i
i 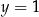 B)
B) 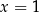 i
i 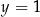 C)
C) 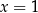 i
i 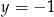 D)
D) 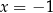 i
i 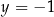
Układ równań 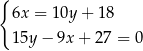
A) ma dokładnie jedno rozwiązanie. B) ma dwa rozwiązania.
C) ma nieskończenie wiele rozwiązań. D) nie ma rozwiązań.
Układ równań 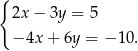
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 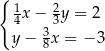
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 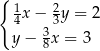
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Układ równań 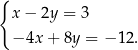
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 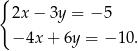
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 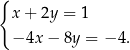
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Układ równań 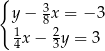
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma nieskończenie wiele rozwiązań.
Pary liczb 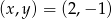 i
i 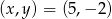 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 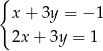 B)
B) 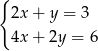 C)
C) 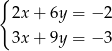 D)
D) 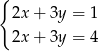
Pary liczb 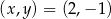 i
i 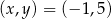 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 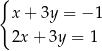 B)
B) 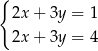 C)
C) 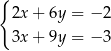 D)
D) 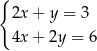
Ania ma w skarbonce 99 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy więcej niż pięciozłotowych.
Jeżeli przez  oznaczymy liczbę monet pięciozłotowych, a przez
oznaczymy liczbę monet pięciozłotowych, a przez 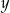 – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
– liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
A) 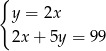 B)
B) 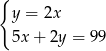 C)
C) 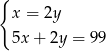 D)
D) 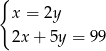
Piotrek ma w skarbonce  monet dwuzłotowych i
monet dwuzłotowych i 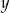 pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 27 złotych. Podane informacje przedstawia układ
pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 27 złotych. Podane informacje przedstawia układ
A) 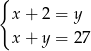 B)
B) 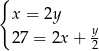 C)
C) 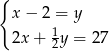 D)
D) 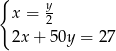
Piotrek ma w skarbonce  monet dwuzłotowych i
monet dwuzłotowych i 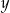 pięćdziesięciogroszówek. Dwuzłotówek jest o trzy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 52 złotych. Podane informacje przedstawia układ
pięćdziesięciogroszówek. Dwuzłotówek jest o trzy więcej od pięćdziesięciogroszówek, a wszystkie monety dają kwotę 52 złotych. Podane informacje przedstawia układ
A) 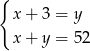 B)
B) 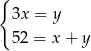 C)
C) 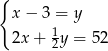 D)
D) 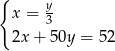
Piotrek ma w skarbonce  monet dwuzłotowych i
monet dwuzłotowych i 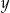 pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy mniej niż pięćdziesięciogroszówek, a wszystkie monety dają kwotę 36 złotych. Podane informacje przedstawia układ
pięćdziesięciogroszówek. Dwuzłotówek jest dwa razy mniej niż pięćdziesięciogroszówek, a wszystkie monety dają kwotę 36 złotych. Podane informacje przedstawia układ
A) 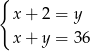 B)
B) 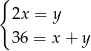 C)
C) 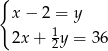 D)
D) 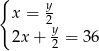
Tomek ma w skarbonce 156 zł w monetach o nominałach 2 zł i 5 zł. Monet dwuzłotowych jest 2 razy mniej niż pięciozłotowych.
Jeżeli przez  oznaczymy liczbę monet pięciozłotowych, a przez
oznaczymy liczbę monet pięciozłotowych, a przez 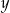 – liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
– liczbę monet dwuzłotowych, to podane zależności opisuje układ równań
A) 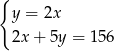 B)
B) 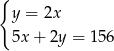 C)
C) 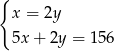 D)
D) 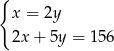
Zmieszano dwa gatunki herbaty, droższą i tańszą, w stosunku 2:3. Cena jednego kilograma tej herbacianej mieszanki wynosi 110 zł. Gdyby te herbaty zmieszano w stosunku 1:4, to cena za 1 kg tej mieszanki wynosiłaby 80 zł. Na podstawie podanych informacji zapisano poniższy układ równań.
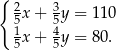
Co oznacza  w tym układzie równań?
w tym układzie równań?
A) Cenę 1 kg herbaty droższej. B) Cenę 1 kg herbaty tańszej.
C) Cenę 5 kg herbaty droższej. D) Cenę 5 kg herbaty tańszej.
Zmieszano dwa gatunki kawy, droższą i tańszą, w stosunku 1:4. Cena jednego kilograma tej mieszanki kaw wynosi 110 zł. Gdyby te kawy zmieszano w stosunku 2:3, to cena za 1 kg tej mieszanki wynosiłaby 120 zł. Na podstawie podanych informacji zapisano poniższy układ równań.
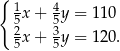
Co oznacza 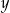 w tym układzie równań?
w tym układzie równań?
A) Cenę 1 kg kawy droższej. B) Cenę 1 kg kawy tańszej.
C) Cenę 5 kg kawy droższej. D) Cenę 5 kg kawy tańszej.
Dane są trzy równania
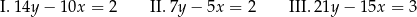
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Układ równań złożony z równań I i III ma jedno rozwiązanie. | P | F |
| Układ równań złożony z równań II i III nie ma rozwiązań. | P | F |
Rozwiązaniem układu równań 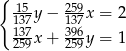 jest para liczb
jest para liczb
A) 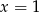 i
i 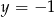 B)
B) 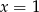 i
i 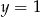 C)
C) 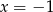 i
i 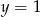 D)
D) 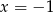 i
i 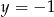
Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości  i
i 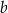 jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 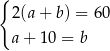 B)
B) 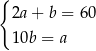 C)
C) 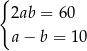 D)
D) 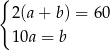
Rozważmy treść następującego zadania:
Pole prostokąta o bokach długości  i
i 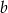 jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 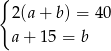 B)
B) 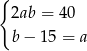 C)
C) 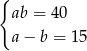 D)
D) 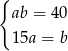
Ania jest 4 razy starsza od Pawła. Za 8 lat Ania i Paweł będą mieli w sumie 38 lat. Jeżeli przez  oznaczymy wiek Pawła, a przez
oznaczymy wiek Pawła, a przez 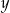 wiek Ani, to powyższą sytuację opisuje układ równań
wiek Ani, to powyższą sytuację opisuje układ równań
A) 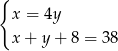 B)
B) 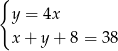 C)
C) 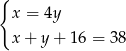 D)
D) 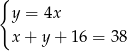
Rozważmy treść następującego zadania:
Obwód rombu o przekątnych długości  i
i 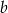 jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
Który układ równań opisuje zależności między długościami przekątnych tego rombu?
A) 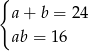 B)
B) 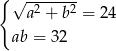 C)
C) 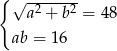 D)
D) 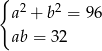
Układ równań 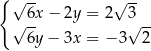
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C)ma nieskończenie wiele rozwiązań. D) ma dokładnie dwa rozwiązania.
Rozwiązaniem układu równań 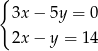 jest para
jest para 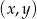 liczb takich, że
liczb takich, że
A) 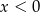 i
i 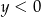 B)
B) 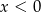 i
i 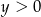 C)
C) 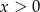 i
i 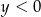 D)
D) 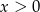 i
i 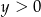
Rozwiązaniem układu równań 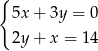 jest para
jest para 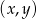 liczb takich, że
liczb takich, że
A) 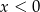 i
i 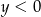 B)
B) 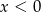 i
i 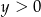 C)
C) 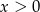 i
i 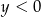 D)
D) 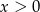 i
i 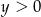
Rozwiązaniem układu równań 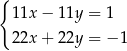 jest para liczb:
jest para liczb: 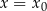 ,
, 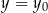 . Wtedy
. Wtedy
A) 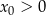 i
i 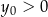 B)
B) 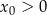 i
i 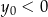 C)
C) 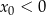 i
i 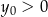 D)
D) 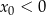 i
i 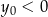
Rozwiązanie 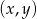 układu równań
układu równań 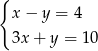 spełnia warunki
spełnia warunki
A) 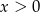 i
i 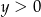 B)
B) 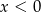 i
i 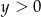 C)
C) 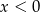 i
i 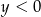 D)
D) 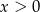 i
i 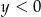
Rozwiązanie 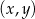 układu równań
układu równań 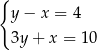 spełnia warunki
spełnia warunki
A) 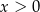 i
i 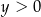 B)
B) 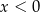 i
i 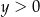 C)
C) 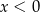 i
i 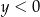 D)
D) 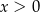 i
i 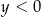
Para liczb 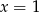 i
i 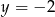 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 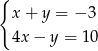 B)
B) 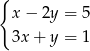 C)
C) 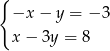 D)
D) 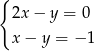
Para liczb 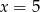 i
i 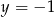 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 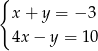 B)
B) 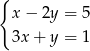 C)
C) 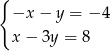 D)
D) 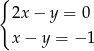
Para liczb 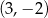 spełnia układ równań
spełnia układ równań
A) 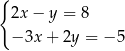 B)
B) 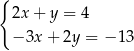
C) 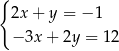 D)
D) 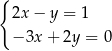
Para liczb 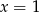 i
i 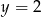 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 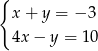 B)
B) 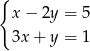 C)
C) 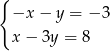 D)
D) 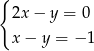
Para liczb 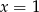 i
i 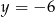 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 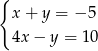 B)
B) 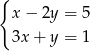 C)
C) 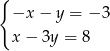 D)
D) 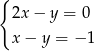
Dany jest układ równań
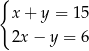
Liczby  i
i 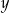 spełniające ten układ równań spełniają też warunek:
spełniające ten układ równań spełniają też warunek:
A)  i
i 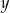 są liczbami parzystymi. B)
są liczbami parzystymi. B)  i
i 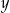 są liczbami ujemnymi.
są liczbami ujemnymi.
C) suma  i
i 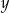 jest podzielna przez 3. D) różnica
jest podzielna przez 3. D) różnica  i
i 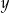 jest równa 0.
jest równa 0.
Dany jest układ równań
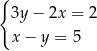
Liczby  i
i 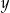 spełniające ten układ równań spełniają też warunek:
spełniające ten układ równań spełniają też warunek:
A)  i
i 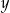 są liczbami parzystymi. B)
są liczbami parzystymi. B)  i
i 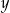 są liczbami ujemnymi.
są liczbami ujemnymi.
C) suma  i
i 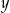 jest podzielna przez 3. D) różnica
jest podzielna przez 3. D) różnica  i
i 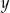 jest liczbą pierwszą.
jest liczbą pierwszą.
W klasie IIIa stosunek liczby chłopców do dziewcząt jest równy 3:2, a w klasie IIIb jest dwa razy więcej dziewcząt niż chłopców. Łącznie w obu tych klasach jest 24 chłopców i 28 dziewcząt. Na podstawie podanych informacji zapisano poniższy układ równań.
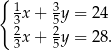
Co oznacza  w tym układzie równań?
w tym układzie równań?
A) Liczbę chłopców w klasie IIIa. B) Liczbę chłopców w klasie IIIb.
C) Liczbę uczniów klasy IIIa. D) Liczbę uczniów klasy IIIb.
Jeżeli 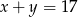 i
i 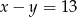 to
to
A) 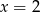 B)
B) 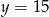 C)
C) 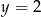 D)
D) 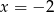
Jeżeli 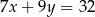 i
i 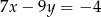 to
to
A) 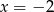 B)
B) 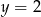 C)
C) 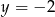 D)
D)