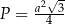Wykonano następującą konstrukcję.
1. Narysowano romb 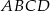 .
.
2. Wykreślono przekątne rombu i ich punkt przecięcia oznaczono literą 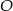 .
.
3. Poprowadzono prostą prostopadłą do boku 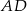 i przechodzącą przez punkt
i przechodzącą przez punkt 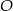 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 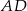 oznaczono literą
oznaczono literą 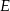 .
.
4. Narysowano okrąg o środku w punkcie 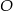 i promieniu
i promieniu 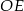 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego rombu.
B) jest styczny do wszystkich boków tego rombu.
C) jest styczny do przekątnych tego rombu.
D) nie ma punktów wspólnych z jednym z boków rombu.
/Szkoła podstawowa/Zadania testowe/Geometria/Romb
Punkt 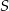 jest środkiem okręgu wpisanego w romb
jest środkiem okręgu wpisanego w romb 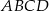 . Okrąg ten jest styczny do boku
. Okrąg ten jest styczny do boku 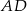 w punkcie
w punkcie 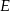 oraz
oraz 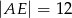 ,
, 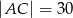 .
.
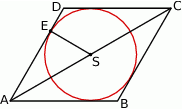
Promień 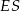 okręgu ma długość
okręgu ma długość
A) 12 B) 9 C) 8 D) 6
Kąt ostry rombu ma miarę 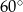 , a bok tego rombu ma długość równą 4 cm. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, a bok tego rombu ma długość równą 4 cm. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Krótsza przekątna dzieli ten romb na dwa trójkąty równoboczne. | P | F |
Pole tego rombu jest równe 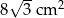 . . | P | F |
Kąt ostry rombu ma miarę 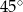 , a bok tego rombu ma długość równą 4 cm. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, a bok tego rombu ma długość równą 4 cm. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Krótsza przekątna dzieli ten romb na dwa trójkąty prostokątne. | P | F |
Pole tego rombu jest równe 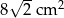 . . | P | F |
Przekątne rombu mają długości 24 i 10. Jaka jest długość boku rombu?
A) 13 B) 26 C) 6,5 D) 14
Pole rombu jest równe 36, a jedna z jego przekątnych jest dwa razy krótsza od drugiej.
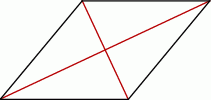
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt ostry rombu ma miarę 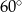 | P | F |
Bok rombu ma długość 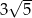 . . | P | F |
Bok rombu ma długość 17 cm, a jedna z jego przekątnych ma długość 30 cm. Pole tego rombu jest równe
A) 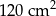 B)
B) 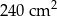 C)
C) 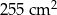 D)
D) 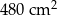
Bok rombu ma długość 26 cm, a jedna z jego przekątnych ma długość 48 cm. Pole tego rombu jest równe
A) 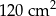 B)
B) 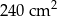 C)
C) 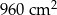 D)
D) 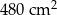
W pewnym rombie jeden z kątów wewnętrznych ma miarę 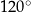 . Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
A) 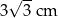 B) 6 cm C)
B) 6 cm C) 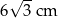 D) 12 cm
D) 12 cm
W pewnym rombie jeden z kątów wewnętrznych ma miarę 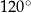 . Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
A) 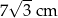 B) 7 cm C)
B) 7 cm C) 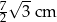 D) 14 cm
D) 14 cm
W pewnym rombie jeden z kątów wewnętrznych ma miarę 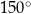 . Pole tego rombu jest równe
. Pole tego rombu jest równe 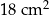 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bok rombu jest dwa razy dłuższy od jego wysokości. | P | F |
| Obwód tego rombu jest równy 27 cm. | P | F |
Kąt ostry rombu ma miarę 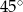 , a wysokość rombu jest równa
, a wysokość rombu jest równa 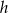 .
.
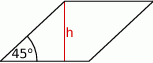
Pole tego rombu można wyrazić wzorem
A) 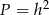 B)
B) 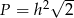 C)
C) 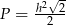 D)
D) 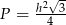
Kąt ostry rombu ma miarę 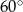 , a wysokość rombu jest równa
, a wysokość rombu jest równa 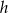 .
.
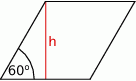
Pole tego rombu można wyrazić wzorem
A) 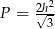 B)
B) 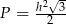 C)
C) 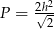 D)
D) 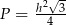
Dany jest romb, którego przekątne mają długość 24 cm i 18 cm. Pole tego rombu jest równe
A) 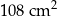 B)
B) 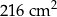 C)
C) 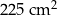 D)
D) 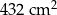
Na rysunku przedstawiono romb i jego przekątne. Długości odcinków na jakie dzielą się przekątne tego rombu są opisane za pomocą wyrażeń.
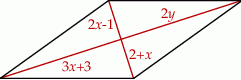
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód rombu jest równy 52. | P | F |
| Pole rombu jest równe 240. | P | F |
Kąt ostry rombu ma miarę 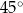 , a jego bok ma długość
, a jego bok ma długość  .
.
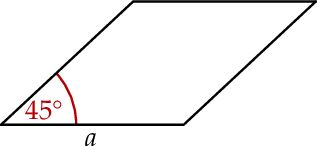
Pole tego rombu można wyrazić wzorem
A) 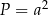 B)
B) 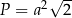 C)
C) 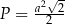 D)
D)