W urnie znajdują się kule czarne, białe i niebieskie, przy czym są co najmniej dwie kule każdego koloru i w sumie jest 15 kul. Losujemy z urny trzy kule. Rozważmy następujące zdarzenia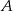 
– wylosowano trzy kule tego samego koloru;
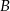– żadne dwie z wylosowanych kul nie są tego samego koloru.
Oblicz prawdopodobieństwo zdarzenia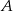 
jeżeli prawdopodobieństwo zdarzenia 
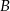jest równe 
.
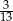/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna
W pierwszej urnie znajduje się 5 kul białych i 17 kul czarnych. W drugiej urnie znajduje się 16 kul białych i 34 kule czarne. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Ukryj
Podobne zadania
W pierwszej urnie znajdują się 4 kule białe i 13 kul czarnych. W drugiej urnie znajduje się 17 kul białych i 26 kul czarnych. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę białą. Wynik przedstaw w postaci ułamka nieskracalnego.
Ukryj
Podobne zadania
Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej.
Ukryj
Podobne zadania
W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej lub czerwonej.
W urnie znajdują się kule białe, zielone i czerwone. Kul zielonych jest dwa razy więcej niż kul białych, a kul czerwonych jest 3 razy więcej niż białych. Wyjęto dwa razy po jednej kuli bez zwracania. Oblicz liczbę kul białych w urnie, jeśli prawdopodobieństwo wylosowania dwóch kul zielonych jest równe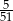 
.
Z urny, w której znajduje się 20 kul białych i 2 czarne losujemy 
kul. Znajdź najmniejszą wartość 
, taką przy której prawdopodobieństwo wylosowania przynajmniej jednej kuli czarnej jest większe od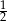 
.
Co czwarta kula w urnie to biała, pozostałe mają kolor czarny lub niebieski. Losujemy jedna kulę. Prawdopodobieństwo wylosowania kuli niebieskiej lub białej jest dwukrotnie mniejsze niż prawdopodobieństwo wylosowania kuli niebieskiej lub czarnej. Oblicz prawdopodobieństwo wylosowania kuli czarnej.
Z urny zawierającej 10 kul ponumerowanych kolejnymi liczbami od 1 do 10 losujemy jednocześnie trzy kule. Oblicz prawdopodobieństwo zdarzenia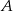 
polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.
Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.
Ukryj
Podobne zadania
Z urny, w której jest 7 kul czarnych i 3 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule różnych kolorów.
Z urny, w której jest 5 kul czerwonych i 7 czarnych wyjęto dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wyjęto kule w różnych kolorach.
Z urny, w której jest 6 kul czarnych i 2 zielone, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule różnych kolorów.
W urnie znajduje się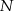 
losów, przy czym 
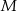z nich to losy wygrywające (
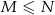). Wybieramy losowo 
losów z urny (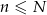
) i niech 
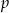oznacza prawdopodobieństwo, że dokładnie 
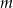spośród tych losów to losy wygrywające (
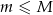oraz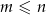 
). Uzasadnij, że
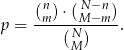
W urnie jest pewna liczba kul białych i jedna kula czarna. Losujemy jedną kulę z tej urny, zatrzymujemy ją, a następnie z pozostałych kul losujemy jedną kulę. Ile powinno być kul białych w urnie, aby prawdopodobieństwo wylosowania dwóch kul białych było równe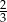 
?
