W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od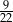 
.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Urna
W urnie znajdują się 52 kule, które mogą się różnić wyłącznie kolorem. Wśród nich jest 26 kul białych, 6 kul czarnych, 12 niebieskich i 8 zielonych. Z tej urny losujemy czterokrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania czterech kul, wśród których są 2 białe i 2 niebieskie. Wynik podaj w postaci ułamka nieskracalnego.
W urnie znajduje się 16 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 10 kul białych i 6 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul białych.
Ukryj
Podobne zadania
W urnie znajduje się 18 kul, które mogą się różnić wyłącznie kolorem. Wśród nich jest 6 kul białych i 12 kul czarnych. Z tej urny losujemy dwukrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania dwóch kul czarnych.
W urnie znajduje się dwa razy więcej kul białych niż czarnych. Losujemy z urny jednocześnie dwie kule. Prawdopodobieństwo wylosowania obu kul białych jest równe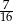 
. Oblicz prawdopodobieństwo wylosowania kul różnych kolorów.
W urnie znajduje się 5 kul białych i 3 czarne. Wyjmujemy losowo 4 kule. Oblicz prawdopodobieństwo, że wśród wyjętych są przynajmniej 2 kule czarne.
W jednej urnie są 3 kule: czerwona, biała i zielona, a w drugiej urnie są 2 kule: czerwona i biała. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
Ukryj
Podobne zadania
W jednej urnie są 4 kule: czerwona, biała, niebieska i zielona, a w drugiej urnie są 3 kule: czerwona, biała i zielona. Losujemy po jednej kuli z każdej urny. Jakie jest prawdopodobieństwo wyciągnięcia dwóch kul w tym samym kolorze?
W urnie jest pewna liczba kul białych i pewna liczba kul czarnych – razem 9 kul. Ile jest kul białych w urnie, jeśli wiadomo, że przy jednoczesnym losowaniu dwóch kul z tej urny prawdopodobieństwo otrzymania kul tego samego koloru jest równe prawdopodobieństwu otrzymania kul różnych kolorów?
Ile maksymalnie kul zielonych można włożyć do urny, w której jest 7 kul czerwonych, aby prawdopodobieństwo wylosowania 2 kul różnokolorowych było większe lub równe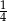 
?
Liczby kul białych, niebieskich i czerwonych tworzą - w podanej kolejności - ciąg arytmetyczny o różnicy 2. Spośród tych kul losujemy jednocześnie trzy. Prawdopodobieństwo wylosowania trzech kul, z których każda jest innego koloru wynosi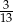 
. Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.
W każdej z czterech urn są 24 kule, w tym dokładnie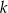 
białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości 
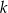prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.
W urnie znajduje się 20 kul: 9 białych, 9 czerwonych i 2 zielone. Z tej urny losujemy bez zwracania 3 kule. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że co najmniej dwie z wylosowanych kul są tego samego koloru.
Ukryj
Podobne zadania
W urnie jest dziesięć kul różniących się wyłącznie kolorem: 4 czarne, 3 białe, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przynajmniej dwie z wylosowanych kul mają ten sam kolor.
W jednej urnie jest 5 kul białych i pewna liczba kul czarnych, w drugiej zaś 6 kul czarnych i pewna liczba kul białych. Z każdej urny losujemy po dwie kule. Prawdopodobieństwo wylosowania jednocześnie dwóch kul białych z pierwszej urny jest większe od 
, a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od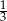 
. W której urnie jest więcej kul białych, a w której czarnych?
Z urny zawierającej 8 kul białych i 4 czarne wylosowano bez zwracania 5 kul. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu?
Ukryj
Podobne zadania
Z urny zawierającej 7 kul białych i 3 kule czarne wylosowano bez zwracania 4 kule. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu?
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowana kula jest czerwona lub zielona.
Ukryj
Podobne zadania
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowano kulę czerwoną lub kulę z numerem parzystym.
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że numer wylosowanej kuli jest podzielny przez 3.
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowano kulę zieloną z numerem dwucyfrowym.
W urnie znajduje się 
kul czarnych i 
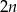kul białych (
, 
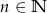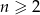). Losujemy jednocześnie dwie kule. Dla jakich 
prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?
W urnie znajdują się drewniane klocki, przy czym każdy z klocków jest biały lub czarny oraz każdy z klocków ma kształt kuli lub sześcianu. Wiadomo, że prawdopodobieństwo wylosowania czarnego klocka jest równe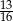 
, prawdopodobieństwo wylosowania klocka w kształcie sześcianu jest równe 
, a prawdopodobieństwo wylosowania klocka, który jest biały lub jest kulą jest równe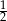 
. Oblicz prawdopodobieństwo wybrania klocka, który jest białą kulą.
W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych. Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi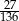 
. Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.
W urnie są 3 kule białe, 4 czarne i 5 zielonych. Losujemy ze zwracaniem 3 kule. Oblicz prawdopodobieństwo tego, że wśród wylosowanych kul będą kule biała i czarna.
W urnie jest 15 kartek, ponumerowanych liczbami od 1 do 15. Wyciągamy 5 kartek bez zwracania. Jakie jest prawdopodobieństwo, że numer trzeciej kartki jest liczbą podzielną przez 3 i jednocześnie numer piątej kartki jest liczbą podzielną przez 5?
W urnie jest dziesięć kul: 4 białe, 3 czarne, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród wylosowanych kul nie ma kul w tym samym kolorze. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
