Podstawą ostrosłupa  jest kwadrat
jest kwadrat  (patrz rysunek).
(patrz rysunek).
Krawędź 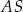 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 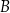 od krawędzi
od krawędzi 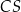 jest równa
jest równa 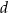 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 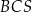 i
i 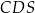 ma miarę
ma miarę 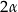 , gdzie
, gdzie 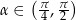 . Oblicz:
. Oblicz:
-
odległość punktu
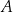 od krawędzi
od krawędzi 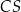
-
wysokość tego ostrosłupa.

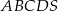 jest kwadrat
jest kwadrat 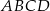 . Krawędź boczna
. Krawędź boczna 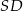 jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi
jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi 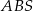 i
i 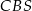 tego ostrosłupa.
tego ostrosłupa. 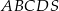 jest kwadrat
jest kwadrat 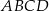 o boku długości
o boku długości  , a krawędź boczna
, a krawędź boczna 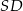 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi 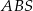 i
i 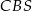 tego ostrosłupa jest równy
tego ostrosłupa jest równy 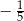 .
. 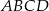 o boku długości 25. Ściany boczne
o boku długości 25. Ściany boczne 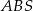 i
i 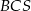 mają takie same pola, każde równe 250. Ściany boczne
mają takie same pola, każde równe 250. Ściany boczne 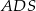 i
i 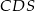 też mają jednakowe pola, każde równe 187,5. Krawędzie boczne
też mają jednakowe pola, każde równe 187,5. Krawędzie boczne 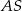 i
i 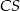 mają równe długości. Oblicz objętość tego ostrosłupa.
mają równe długości. Oblicz objętość tego ostrosłupa. 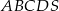 jest kwadrat
jest kwadrat 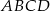 . Trójkąt równoramienny
. Trójkąt równoramienny 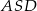 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 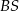 ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny
ma długość 17. Oblicz cosinus kąta nachylenia płaszczyzny 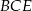 do płaszczyzny podstawy, gdzie
do płaszczyzny podstawy, gdzie 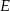 jest środkiem krawędzi
jest środkiem krawędzi 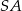 .
. 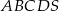 jest kwadrat
jest kwadrat 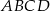 . Pole trójkąta równoramiennego
. Pole trójkąta równoramiennego 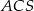 jest równe 120 oraz
jest równe 120 oraz 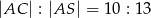 . Oblicz pole powierzchni bocznej tego ostrosłupa.
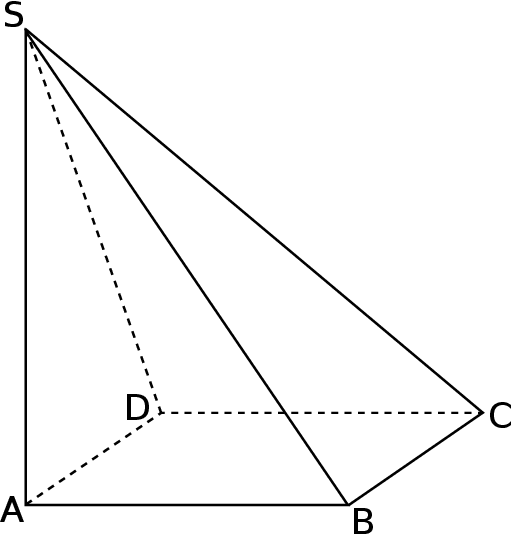
. Oblicz pole powierzchni bocznej tego ostrosłupa. 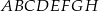 przekątna
przekątna 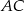 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 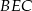 jest równy
jest równy 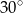 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 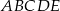 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku. 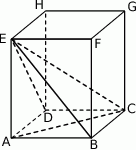
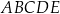 jest kwadrat o boku długości 12. Spodek
jest kwadrat o boku długości 12. Spodek 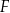 wysokości
wysokości 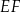 ostrosłupa jest środkiem krawędzi
ostrosłupa jest środkiem krawędzi 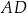 . Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi
. Wiedząc, że dwie krótsze krawędzie boczne mają tę samą długość, równą 10, oblicz tangens kąta nachylenia krawędzi 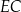 do płaszczyzny podstawy.
do płaszczyzny podstawy. 
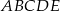 jest kwadrat
jest kwadrat 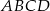 . Punkt
. Punkt 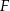 jest środkiem krawędzi
jest środkiem krawędzi 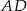 , odcinek
, odcinek 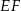 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że 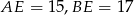 .
. 
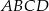 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych  ,
, 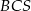 ,
, 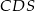 i
i 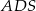 są odpowiednio równe: 740,
są odpowiednio równe: 740, 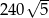 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa. 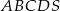 jest kwadrat
jest kwadrat 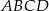 o boku długości 4. Odcinek
o boku długości 4. Odcinek 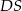 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 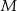 jest środkiem odcinka
jest środkiem odcinka 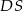 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 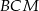 .
. 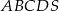 jest kwadrat
jest kwadrat 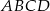 . Trójkąt równoramienny
. Trójkąt równoramienny 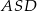 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 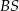 ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną
ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 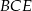 , gdzie
, gdzie 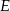 jest środkiem krawędzi
jest środkiem krawędzi 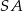 .
.  przekątna
przekątna 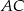 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 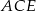 jest równy
jest równy 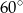 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 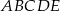 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.