Na dowodzenie/Geometryczny - zadania z matematyki

/Szkoła średnia/Ciągi/Geometryczny/Na dowodzenie

Dany jest ciąg geometryczny 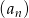(an) o pierwszym wyrazie równym 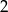, i ilorazie równym 10. Wykaż, że wszystkie punkty o współrzędnych 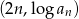(2n ,lo gan) leżą na jednej prostej.

Wykaż, że jeżeli ciąg 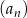(an) jest ciągiem geometrycznym, to

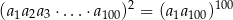
2 100 (a1a2a3 ⋅ ...⋅a100) = (a1a100)

Uzasadnij, że ciąg określony wzorem 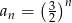(3)n an = 2 jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.

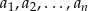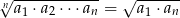Liczby a1,a2,...,an są dodatnie i w podanej kolejności tworzą ciąg geometryczny. Uzasadnij, że prawdziwa jest równość √ ------------ √ ------ na1 ⋅a2⋅⋅⋅an = a1 ⋅ an .

Liczby dodatnie 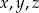x,y ,z są wyrazami ciągu geometrycznego o numerach równych odpowiednio 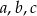a,b,c , a liczby 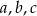a,b,c są kolejnymi wyrazami ciągu geometrycznego. Wykaż, że

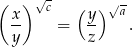
( ) √- √- x c ( y) a -- = -- . y z

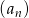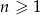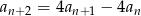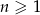Ciąg geometryczny (an ) , gdzie n ≥ 1 spełnia warunek an+2 = 4an +1 − 4an dla n ≥ 1 . Uzasadnij, że ciąg ten spełnia też warunek 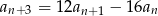an+ 3 = 12an+ 1 − 16an dla n ≥ 1 .

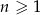Udowodnij, że jeżeli cztery liczby dodatnie 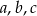a,b ,c i 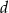są kolejnymi wyrazami ciągu geometrycznego, to a+ d ≥ b + c .

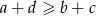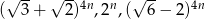Wykaż, że dla każdej liczby naturalnej , liczby √ -- √ --4n n √ -- 4n ( 3+ 2) ,2 ,( 6 − 2) są kolejnymi wyrazami ciągu geometrycznego.

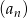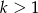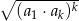Udowodnij, że w ciągu geometrycznym (an) o wyrazach dodatnich iloczyn k > 1 początkowych wyrazów ciągu jest równy ∘ --------- (a1 ⋅ak)k .

Wykaż, że jeżeli 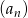(an) jest ciągiem geometrycznym, to ciąg 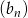(bn) o wyrazie ogólnym określonym wzorem 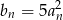bn = 5a2n też jest ciągiem geometrycznym.

Ukryj Podobne zadania

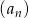Ciąg (an) jest ciągiem geometrycznym. Wykaz, że ciąg 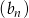(bn) określony wzorem 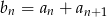bn = an + an +1 jest również ciągiem geometrycznym.

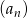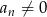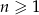Wyrazy ciągu geometrycznego (an) , w którym an ⁄= 0 dla n ≥ 1 spełniają warunek

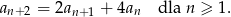
an+ 2 = 2an+1 + 4an dla n ≥ 1.

Wykaż, że wyrazy tego ciągu spełniają również warunek

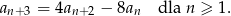
an+ 3 = 4an+2 − 8an dla n ≥ 1.

Udowodnij, że jeżeli liczby 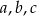a,b,c są kolejnymi wyrazami ciągu geometrycznego, to

(a − b + c)(a + b + c) = a2 + b2 + c2.

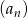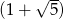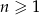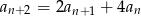Iloraz ciągu geometrycznego (an) jest równy √ -- (1 + 5) . Uzasadnij, że dla każdej liczby naturalnej n ≥ 1 prawdziwy jest wzór an+ 2 = 2an+1 + 4an .

Liczby niezerowe 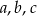a,b,c są wyrazami ciągu geometrycznego o numerach odpowiednio 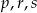p ,r,s . Oblicz wartość wyrażenia

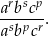
r s p a-b-c-. asbpcr

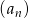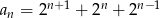Ciąg (an) określony jest wzorem n+ 1 n n−1 an = 2 + 2 + 2 .

Oblicz pierwszy i trzeci wyraz tego ciągu.
Uzasadnij, korzystając z deﬁnicji ciągu geometrycznego, że ciąg 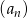jest geometryczny.

Udowodnij że w ciągu geometrycznym o parzystej liczbie wyrazów stosunek sumy wyrazów stojących na miejscach parzystych do sumy wyrazów stojących na miejscach nieparzystych jest równy ilorazowi tego ciągu.

Uzasadnij, że ciąg określony wzorem 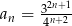32n+-1 an = 4n+2 jest ciągiem geometrycznym. Wyznacz iloraz osiemnastego wyrazu tego ciągu przez wyraz 16.