Pole powierzchni całkowitej graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy  wyraża się wzorem
wyraża się wzorem 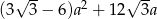 . Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.
. Wyznacz sumę długości krawędzi podstawy i wysokości tego graniastosłupa.
/Szkoła średnia/Geometria/Stereometria/Graniastosłup/Prawidłowy sześciokątny
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez dłuższą przekątną dolnej podstawy oraz przez jedną z krawędzi górnej podstawy. Płaszczyzna ta wyznacza przekrój graniastosłupa, który jest trapezem równoramiennym. Wiedząc, że w trapez ten można wpisać okrąg o promieniu 1, oblicz objętość graniastosłupa.
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Oblicz cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa.
Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 5 cm, zaś najdłuższa przekątna graniastosłupa jest 4 razy dłuższa od najkrótszej przekątnej podstawy.
Oblicz wysokość graniastosłupa sześciokątnego prawidłowego, wiedząc, że krawędź podstawy ma długość 4 cm, zaś najdłuższa przekątna graniastosłupa jest 5 razy dłuższa od najkrótszej przekątnej podstawy.
W graniastosłupie prawidłowym sześciokątnym 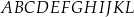 płaszczyzna
płaszczyzna 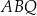 przechodzi przez krawędź
przechodzi przez krawędź 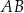 i przez środek
i przez środek 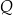 krawędzi
krawędzi 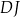 (zobacz rysunek).
(zobacz rysunek).
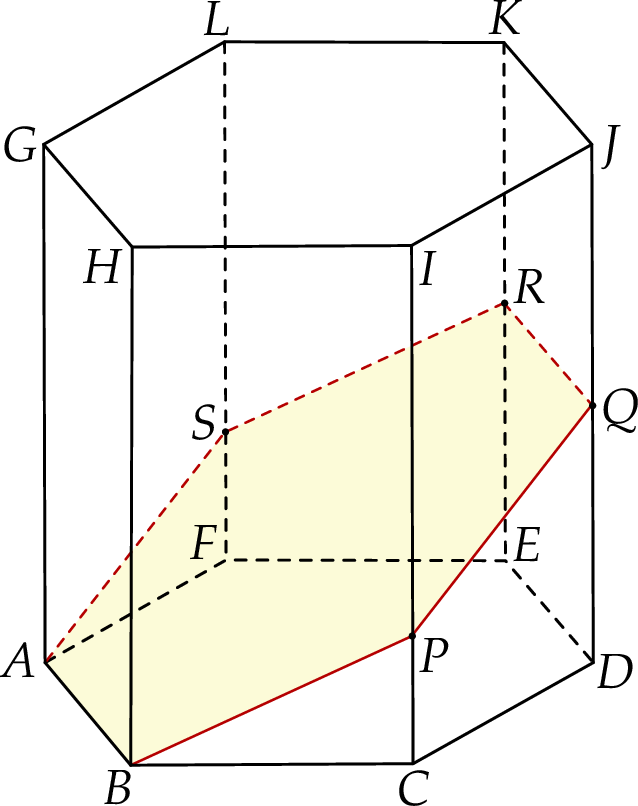
Stosunek pola przekroju graniastosłupa płaszczyzną 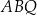 do pola jego podstawy jest równy
do pola jego podstawy jest równy 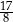 . Oblicz objętość graniastosłupa
. Oblicz objętość graniastosłupa 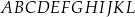 , jeżeli jego krawędź boczna ma długość
, jeżeli jego krawędź boczna ma długość 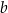 .
.
Pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego jest równe 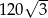 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 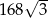 . Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez krawędź podstawy oraz przez środek symetrii graniastosłupa. Płaszczyzna ta wyznacza przekrój o polu równym 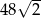 . Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy
. Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy 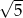 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Krótsza przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt 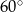 . Przekątna ściany bocznej ma długość
. Przekątna ściany bocznej ma długość 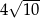 .
.
- Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
- Oblicz cosinus kąta między krótszymi przekątnymi graniastosłupa wychodzącymi z jednego wierzchołka.
W graniastosłupie prawidłowym sześciokątnym płaszczyzna 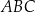 zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem
zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 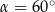 . Pole przekroju graniastosłupa tą płaszczyzną równa się
. Pole przekroju graniastosłupa tą płaszczyzną równa się 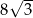 . Zaznacz na poniższym rysunku kąt
. Zaznacz na poniższym rysunku kąt  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
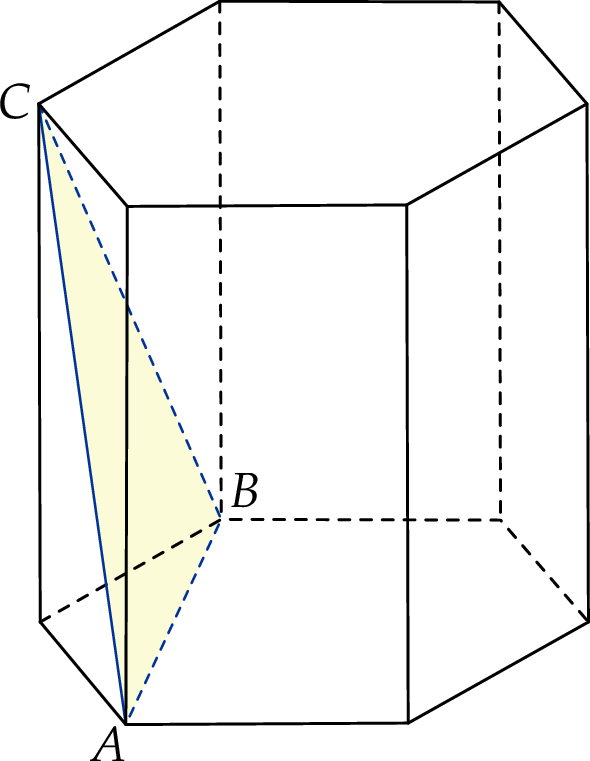
Dany jest graniastosłup prawidłowy sześciokątny o podstawie 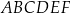 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 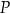 . Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka
. Kąt między przekątnymi ścian bocznych wychodzącymi z wierzchołka 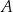 ma miarę
ma miarę 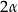 . Objętość tego graniastosłupa jest równa
. Objętość tego graniastosłupa jest równa
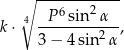
gdzie 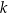 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 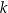 .
.
Krawędź podstawy graniastosłupa prawidłowego sześciokątnego ma długość  . Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa.
. Przekątne sąsiednich ścian bocznych poprowadzone z tego samego wierzchołka są prostopadłe. Oblicz objętość tego graniastosłupa.
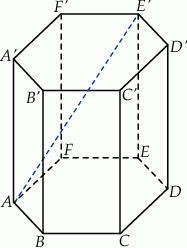
Przekątna 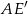 graniastosłupa prawidłowego sześciokątnego ma długość
graniastosłupa prawidłowego sześciokątnego ma długość 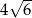 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 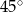 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
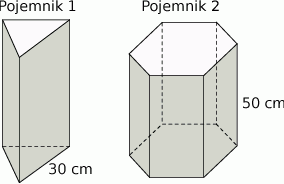
Dwa pojemniki mają kształt graniastosłupów prawidłowych, przy czym pierwszy ma kształt graniastosłupa trójkątnego o krawędzi podstawy długości 30 cm, a drugi sześciokątnego o wysokości 50 cm. Objętość pierwszego pojemnika stanowi 45% objętości drugiego pojemnika i jest mniejsza od tej objętości o 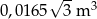 . Oblicz objętości obu pojemników.
. Oblicz objętości obu pojemników.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest dwa razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy.
W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie mają jednakową długość. Oblicz objętość tego graniastosłupa jeżeli jego pole powierzchni całkowitej jest równe 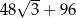 .
.

