Na bokach 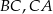 i
i 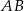 trójkąta
trójkąta 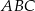 wybrano punkty
wybrano punkty 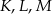 takie, że
takie, że
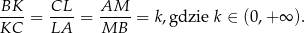
Wyznacz wartość 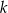 , dla której stosunek pola trójkąta
, dla której stosunek pola trójkąta 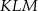 do pola trójkąta
do pola trójkąta 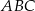 jest najmniejszy.
jest najmniejszy.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na bokach 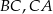 i
i 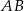 trójkąta
trójkąta 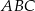 wybrano punkty
wybrano punkty 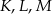 takie, że
takie, że
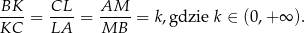
Wyznacz wartość 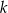 , dla której stosunek pola trójkąta
, dla której stosunek pola trójkąta 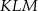 do pola trójkąta
do pola trójkąta 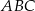 jest najmniejszy.
jest najmniejszy.
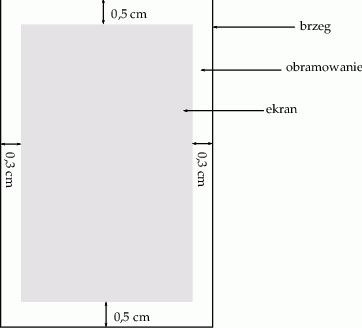
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 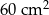 . Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
. Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
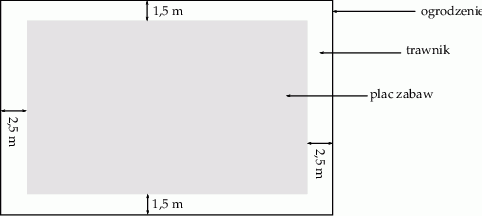
Należy zaprojektować wymiary prostokątnego placu zabaw, tak aby szerokość trawnika wzdłuż dłuższych brzegów placu była równa 1,5 m, a szerokość trawnika wzdłuż krótszych brzegów placu była równa 2,5 m (zobacz rysunek – plac zabaw zaznaczono kolorem szarym). Sam plac zabaw ma mieć powierzchnię 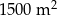 . Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
. Wyznacz takie wymiary placu zabaw, przy których powierzchnia placu wraz z trawnikami jest najmniejsza.
Dany jest odcinek 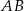 o długości 10. Rozpatrujemy wszystkie sześciokąty foremne
o długości 10. Rozpatrujemy wszystkie sześciokąty foremne 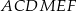 i trójkąty równoboczne
i trójkąty równoboczne 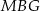 , których wspólny wierzchołek
, których wspólny wierzchołek 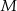 leży na odcinku
leży na odcinku 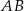 (zobacz rysunek).
(zobacz rysunek).
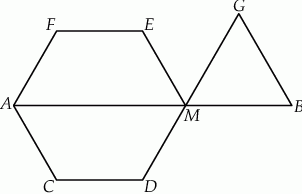
Oblicz stosunek obwodu sześciokąta 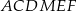 do obwodu trójkąta
do obwodu trójkąta 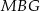 w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.
w przypadku, gdy suma pól tych dwóch wielokątów jest najmniejsza.
Na bokach prostokąta o obwodzie 16 cm opisano, jako na średnicach, półokręgi leżące na zewnątrz prostokąta. Zbadaj, dla jakich długości boków prostokąta, pole figury ograniczonej krzywą złożoną z tych czterech półokręgów jest najmniejsze. Oblicz to pole
Bok kwadratu 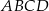 ma długość 1. Na bokach
ma długość 1. Na bokach 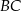 i
i 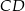 wybrano odpowiednio punkty
wybrano odpowiednio punkty 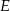 i
i 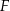 umieszczone tak, by
umieszczone tak, by 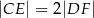 . Oblicz wartość
. Oblicz wartość 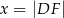 , dla której pole trójkąta
, dla której pole trójkąta 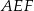 jest najmniejsze.
jest najmniejsze.
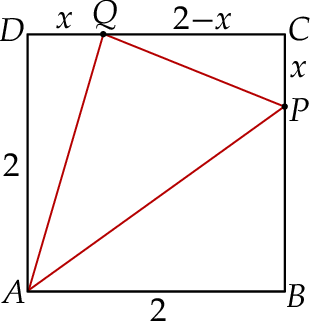
Dany jest kwadrat 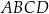 o boku długości 2. Na bokach
o boku długości 2. Na bokach 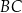 i
i 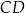 tego kwadratu wybrano – odpowiednio – punkty
tego kwadratu wybrano – odpowiednio – punkty 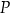 i
i 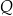 , takie, że długość odcinka
, takie, że długość odcinka 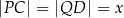 (zobacz rysunek). Wyznacz tę wartość
(zobacz rysunek). Wyznacz tę wartość  , dla której pole trójkąta
, dla której pole trójkąta 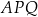 osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
osiąga wartość najmniejszą. Oblicz to najmniejsze pole.
Na kole o promieniu 4 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.
Na kole o promieniu 12 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.
Na kole o promieniu 1 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.
Dany jest trójkąt równoboczny 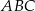 o boku długości
o boku długości  . Punkty
. Punkty 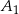 ,
, 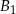 i
i 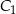 należą do boków
należą do boków 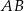 ,
, 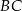 i
i 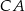 , przy czym
, przy czym 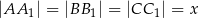 .
.
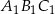 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji.
. Wyznacz dziedzinę tej funkcji.  , dla której pole trójkąta
, dla której pole trójkąta 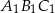 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.Drut o długości 72 cm rozcięto na dwa kawałki i z każdego kawałka zbudowano brzeg trójkąta równoramiennego, przy czym stosunek długości ramienia do długości podstawy w jednym trójkącie wynosi 5:8, a w drugim 13:10. Jakie obwody mają te trójkąty jeżeli suma ich pól jest najmniejsza z możliwych?
Boki 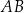 i
i 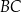 prostokąta
prostokąta 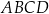 mają długości
mają długości 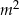 i
i 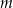 odpowiednio, gdzie
odpowiednio, gdzie 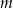 jest ustaloną dodatnią liczbą rzeczywistą. Na bokach
jest ustaloną dodatnią liczbą rzeczywistą. Na bokach 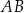 i
i 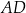 wybrano odpowiednio punkty
wybrano odpowiednio punkty 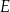 i
i 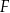 w ten sposób, że
w ten sposób, że 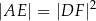 . Oblicz dla jakiej długości odcinka
. Oblicz dla jakiej długości odcinka 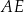 pole trójkąta
pole trójkąta 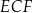 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.
Drut o długości 28 cm należy podzielić na dwie części i z jednej zrobić kwadratową ramkę, a z drugiej ramkę prostokątną, której jeden bok jest trzy razy dłuższy od drugiego. Jak należy podzielić drut, jeżeli chcemy, aby suma pól otrzymanego kwadratu i prostokąta była najmniejsza?
Suma długości dwóch boków trójkąta jest równa 12 cm, a kąt między tymi bokami ma miarę 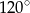 . Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.
. Oblicz jakie powinny być długości boków tego trójkąta aby jego pole było największe.
Obwód trójkąta równobocznego 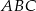 jest równy 12 cm. Punkty
jest równy 12 cm. Punkty 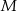 ,
, 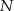 i
i 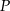 należą odpowiednio do boków
należą odpowiednio do boków 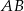 ,
, 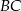 ,
, 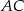 tego trójkąta przy czym
tego trójkąta przy czym 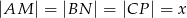 . Zbadaj dla jakiej wartości
. Zbadaj dla jakiej wartości  , pole trójkąta
, pole trójkąta 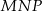 będzie najmniejsze. Znajdź wartość tego pola.
będzie najmniejsze. Znajdź wartość tego pola.
