Dany jest wielomian 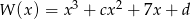 .
.
- Wyznacz wartości współczynników
 i
i 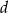 wielomianu
wielomianu 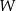 , wiedząc, że jest podzielny przez dwumian
, wiedząc, że jest podzielny przez dwumian 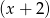 , zaś przy dzieleniu przez dwumian
, zaś przy dzieleniu przez dwumian 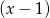 otrzymujemy resztę 3.
otrzymujemy resztę 3. - Dla
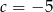 i
i 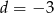 rozwiąż nierówność
rozwiąż nierówność 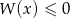 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest wielomian 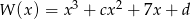 .
.
 i
i 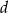 wielomianu
wielomianu 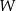 , wiedząc, że jest podzielny przez dwumian
, wiedząc, że jest podzielny przez dwumian 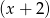 , zaś przy dzieleniu przez dwumian
, zaś przy dzieleniu przez dwumian 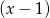 otrzymujemy resztę 3.
otrzymujemy resztę 3. 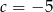 i
i 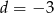 rozwiąż nierówność
rozwiąż nierówność 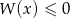 .
.Dla jakich wartości parametru  reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 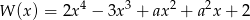 przez dwumian
przez dwumian 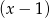 jest większa od 3.
jest większa od 3.
Wyznacz wartości  i
i 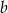 współczynników wielomianu
współczynników wielomianu 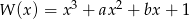 wiedząc, że
wiedząc, że 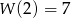 oraz, że reszta z dzielenia
oraz, że reszta z dzielenia 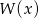 przez
przez 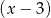 jest równa 10.
jest równa 10.
Jednym z pierwiastków wielomianu 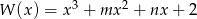 jest liczba 1. Reszta z dzielenia wielomianu
jest liczba 1. Reszta z dzielenia wielomianu 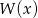 przez dwumian
przez dwumian 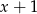 jest równa 4. Oblicz współczynniki
jest równa 4. Oblicz współczynniki 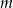 i
i  .
.
Reszty z dzielenia wielomianu 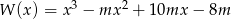 przez dwumiany
przez dwumiany 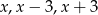 są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru
są kolejnymi wyrazami ciągu arytmetycznego. Oblicz wartość parametru 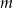 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Wynikiem dzielenia wielomianu 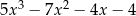 przez dwumian
przez dwumian 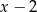 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 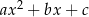 . Oblicz
. Oblicz 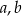 i
i  .
.
Wynikiem dzielenia wielomianu 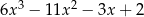 przez dwumian
przez dwumian 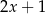 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 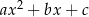 . Oblicz
. Oblicz 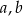 i
i  .
.
W wyniku podzielenia wielomianu 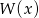 przez
przez 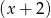 otrzymujemy iloraz
otrzymujemy iloraz 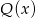 i resztę 0. Jeśli natomiast podzielimy wielomian
i resztę 0. Jeśli natomiast podzielimy wielomian 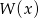 przez
przez 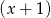 , to otrzymamy iloraz
, to otrzymamy iloraz 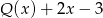 i resztę 2.
i resztę 2.
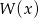 .
. 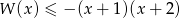 .
.Wielomian 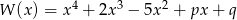 jest podzielny przez dwumian
jest podzielny przez dwumian 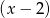 , a przy dzieleniu przez
, a przy dzieleniu przez 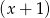 daje resztę
daje resztę 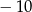 . Wyznacz
. Wyznacz 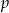 i
i 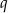 .
.
Wielomian 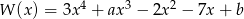 jest podzielny przez dwumian
jest podzielny przez dwumian 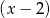 , a przy dzieleniu przez
, a przy dzieleniu przez 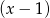 daje resztę 3. Wyznacz
daje resztę 3. Wyznacz  i
i 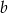 .
.
Wielomian 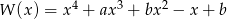 przy dzieleniu przez każdy z dwumianów:
przy dzieleniu przez każdy z dwumianów: 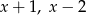 i
i 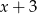 daję tę samą resztę. Wyznacz
daję tę samą resztę. Wyznacz  i
i 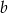 .
.
Wielomian 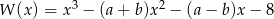 jest podzielny przez dwumian
jest podzielny przez dwumian 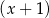 , a reszta z dzielenia wielomianu
, a reszta z dzielenia wielomianu 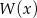 przez dwumian
przez dwumian 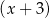 wynosi
wynosi 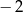 . Oblicz
. Oblicz  i
i 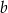 , a następnie rozwiąż nierówność
, a następnie rozwiąż nierówność 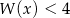 .
.
Wielomian 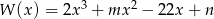 jest podzielny przez każdy z dwumianów
jest podzielny przez każdy z dwumianów 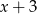 i
i 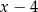 . Oblicz wartości współczynników
. Oblicz wartości współczynników  i
i 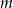 oraz rozwiąż nierówność
oraz rozwiąż nierówność 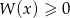 .
.
Wielomian określony wzorem 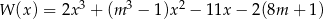 jest podzielny przez dwumian
jest podzielny przez dwumian 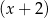 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 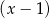 daje resztę 12. Oblicz
daje resztę 12. Oblicz 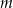 i dla wyznaczonej wartości
i dla wyznaczonej wartości 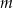 rozwiąż nierówność
rozwiąż nierówność 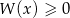 .
.
Wielomian określony wzorem 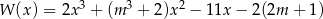 jest podzielny przez dwumian
jest podzielny przez dwumian 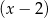 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 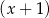 daje resztę 6. Oblicz
daje resztę 6. Oblicz 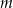 oraz pierwiastki wielomianu
oraz pierwiastki wielomianu 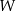 dla wyznaczonej wartości
dla wyznaczonej wartości 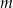 .
.
Wielomian określony wzorem 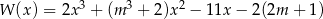 jest podzielny przez dwumian
jest podzielny przez dwumian 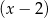 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 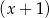 daje resztę 6. Oblicz
daje resztę 6. Oblicz 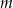 i dla wyznaczonej wartości
i dla wyznaczonej wartości 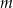 rozwiąż nierówność
rozwiąż nierówność 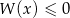 .
.
Dany jest wielomian 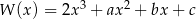 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 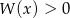 jest zbiór
jest zbiór 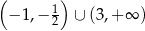 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 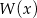 przez dwumian
przez dwumian 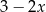 .
.
