Funkcja 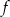 jest określona wzorem
jest określona wzorem 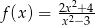 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 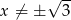 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 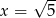 jest równa
jest równa
A) 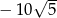 B)
B) 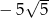 C)
C) 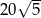 D)
D) 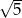
/Szkoła średnia/Zadania testowe/Funkcje/Wymierna/Różne
Funkcja 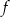 jest określona wzorem
jest określona wzorem 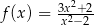 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 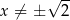 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 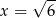 jest równa
jest równa
A) 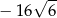 B)
B) 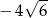 C)
C) 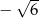 D)
D) 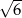
Funkcja 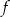 jest określona wzorem
jest określona wzorem 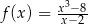 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 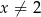 . Wartość pochodnej tej funkcji dla argumentu
. Wartość pochodnej tej funkcji dla argumentu 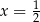 jest równa
jest równa
A) 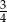 B)
B) 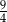 C) 3 D)
C) 3 D) 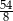
Funkcja 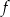 jest określona wzorem
jest określona wzorem 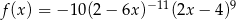 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 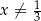 . Wartość funkcji
. Wartość funkcji 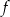 dla argumentu 2019 jest taka sama jak
dla argumentu 2019 jest taka sama jak 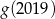 jeżeli
jeżeli
A) 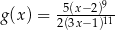 B)
B) 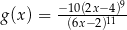
C) 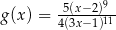 D)
D) 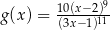
Dana jest funkcja 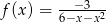 . Wskaż maksymalny zbiór, na którym funkcja
. Wskaż maksymalny zbiór, na którym funkcja 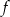 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
A) 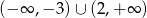 B)
B) 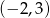 C)
C) 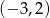 D)
D) 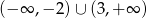
Pochodna funkcji 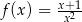 jest równa
jest równa
A) 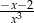 B)
B) 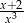 C)
C) 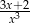 D)
D) 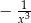
Funkcja 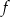 jest określona wzorem
jest określona wzorem 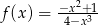 . Wartość tej funkcji dla argumentu równego
. Wartość tej funkcji dla argumentu równego 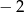 wynosi:
wynosi:
A) 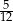 B)
B) 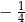 C)
C)  D)
D) 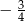
Funkcja 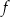 jest określona wzorem
jest określona wzorem 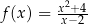 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 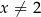 . Wartość funkcji
. Wartość funkcji 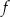 dla argumentu 4 jest równa
dla argumentu 4 jest równa
A) 6 B) 2 C) 10 D) 8
Funkcja 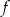 jest określona wzorem
jest określona wzorem 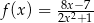 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wartość funkcji
. Wartość funkcji 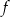 dla argumentu 1 jest równa
dla argumentu 1 jest równa
A) 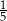 B)
B) 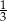 C) 1 D) 2
C) 1 D) 2
Funkcja 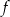 jest określona wzorem
jest określona wzorem 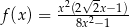 . Wtedy dla argumentu
. Wtedy dla argumentu 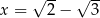 wartość funkcji
wartość funkcji 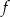 jest równa
jest równa
A) 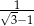 B)
B) 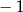 C) 1 D)
C) 1 D) 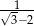
Wartość liczbowa wyrażenia 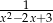 jest największa, gdy liczba
jest największa, gdy liczba  jest równa
jest równa
A) 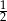 B) 1 C)
B) 1 C) 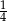 D) 2
D) 2
Wartość liczbowa wyrażenia 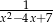 jest największa, gdy liczba
jest największa, gdy liczba  jest równa
jest równa
A) 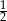 B) 1 C)
B) 1 C) 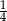 D) 2
D) 2
Wartość liczbowa wyrażenia 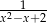 jest największa, gdy liczba
jest największa, gdy liczba  jest równa
jest równa
A) 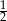 B) 1 C)
B) 1 C) 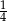 D) 2
D) 2
Funkcja 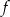 jest określona wzorem
jest określona wzorem 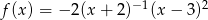 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 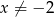 . Wartość funkcji
. Wartość funkcji 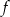 dla argumentu 2 jest równa
dla argumentu 2 jest równa
A) 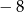 B)
B) 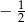 C)
C) 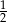 D) 8
D) 8
Funkcja 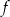 jest określona wzorem
jest określona wzorem 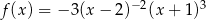 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 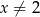 . Wartość funkcji
. Wartość funkcji 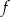 dla argumentu
dla argumentu 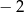 jest równa
jest równa
A) 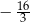 B)
B) 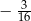 C)
C) 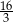 D)
D) 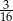
Funkcja 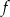 jest określona wzorem
jest określona wzorem 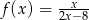 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 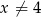 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 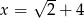 jest równa
jest równa
A) 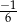 B)
B) 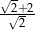 C)
C) 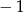 D)
D) 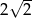
Funkcja 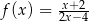 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej 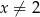 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 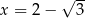 jest równa
jest równa
A)  B)
B) 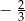 C)
C) 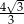 D)
D) 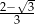
Funkcja 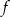 jest określona wzorem
jest określona wzorem 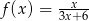 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 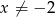 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 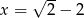 jest równa
jest równa
A) 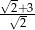 B)
B) 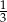 C)
C) 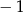 D)
D) 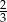
Funkcja 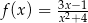 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Pochodna tej funkcji jest określona wzorem
. Pochodna tej funkcji jest określona wzorem
A) 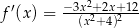 B)
B) 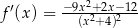
C) 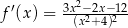 D)
D) 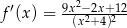
Pochodna 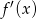 funkcji
funkcji 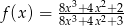 jest określona wzorem
jest określona wzorem
A) 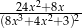 B)
B) 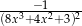 C)
C) 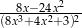 D)
D) 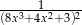
Funkcja 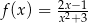 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  . Pochodna tej funkcji jest określona wzorem
. Pochodna tej funkcji jest określona wzorem
A) 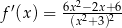 B)
B) 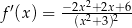
C) 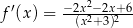 D)
D) 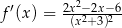
Jeżeli 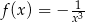 , to
, to
A) 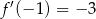 B)
B) 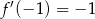 C)
C) 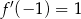 D)
D) 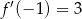
Funkcja 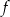 jest określona wzorem
jest określona wzorem 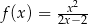 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 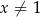 . Wtedy dla argumentu
. Wtedy dla argumentu 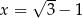 wartość funkcji
wartość funkcji 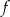 jest równa
jest równa
A) 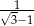 B)
B) 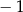 C) 1 D)
C) 1 D) 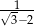
Funkcja 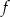 jest określona wzorem
jest określona wzorem 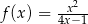 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 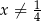 . Wtedy dla argumentu
. Wtedy dla argumentu 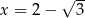 wartość funkcji
wartość funkcji 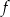 jest równa
jest równa
A) 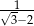 B)
B) 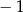 C) 1 D)
C) 1 D) 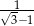
Funkcja 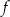 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 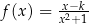 , gdzie
, gdzie 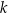 jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek
jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek 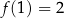 . Wartość współczynnika
. Wartość współczynnika 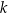 we wzorze tej funkcji jest równa
we wzorze tej funkcji jest równa
A) 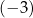 B) 3 C)
B) 3 C) 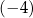 D) 4
D) 4
Funkcja 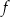 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 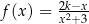 , gdzie
, gdzie 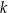 jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek
jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek 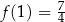 . Wartość współczynnika
. Wartość współczynnika 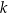 we wzorze tej funkcji jest równa
we wzorze tej funkcji jest równa
A) 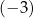 B) 3 C)
B) 3 C) 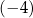 D) 4
D) 4
Wykresy funkcji 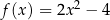 i
i 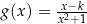 określonych dla każdej liczby rzeczywistej
określonych dla każdej liczby rzeczywistej  przecinają się w dwóch punktach – jednym z nich jest punkt
przecinają się w dwóch punktach – jednym z nich jest punkt 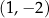 . Liczba
. Liczba 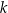 jest równa
jest równa
A) 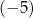 B) 5 C)
B) 5 C) 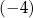 D) 4
D) 4
Funkcja 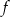 określona jest wzorem
określona jest wzorem 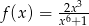 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 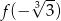 jest równa
jest równa
A) 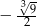 B)
B) 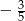 C)
C)  D)
D) 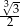
Funkcja 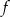 określona jest wzorem
określona jest wzorem 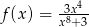 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 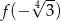 jest równa
jest równa
A) 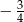 B)
B) 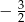 C)
C) 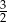 D)
D) 
Funkcja 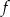 określona jest wzorem
określona jest wzorem 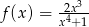 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 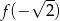 jest równa
jest równa
A) 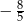 B)
B) 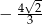 C)
C) 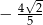 D)
D) 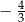
Funkcja 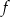 określona jest wzorem
określona jest wzorem 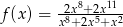 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 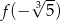 jest równa
jest równa
A) 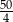 B)
B) 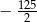 C)
C) 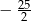 D)
D) 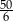
Liczba punktów wspólnych wykresu funkcji wymiernej 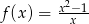 z osią
z osią 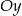 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba punktów wspólnych wykresu funkcji wymiernej 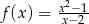 z osią
z osią 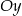 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0

