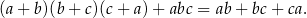Uzasadnij, że dla każdej liczby 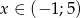 wyrażenie
wyrażenie 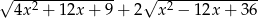 ma stałą wartość.
ma stałą wartość.
/Szkoła średnia/Liczby/Wyrażenia algebraiczne/Udowodnij...
Uzasadnij, że jeżeli  i
i 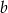 są liczbami całkowitymi i
są liczbami całkowitymi i 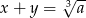 oraz
oraz 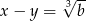 , to
, to 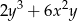 też jest liczbą całkowitą.
też jest liczbą całkowitą.
Udowodnij, że jeżeli liczby niezerowe 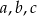 spełniają warunek
spełniają warunek 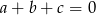 to
to
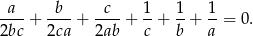
Wykaż, że jeżeli liczby rzeczywiste 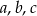 spełniają równość
spełniają równość 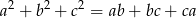 to
to 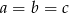 .
.
Wykaż, że jeżeli liczby rzeczywiste  i
i 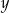 spełniają warunek
spełniają warunek
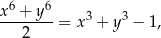
to 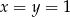 .
.
Wykaż, że jeżeli liczby dodatnie  i
i 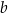 spełniają warunek
spełniają warunek
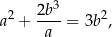
to spełniają też równość
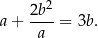
Wykaż, że jeżeli liczby rzeczywiste 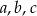 spełniają warunek
spełniają warunek 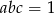 , to
, to
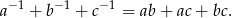
Wykaż, że jeżeli liczby rzeczywiste 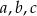 spełniają warunek
spełniają warunek 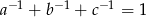 , to
, to
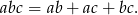
Wykaż, że jeżeli  jest parzystą liczbą całkowitą dodatnią, to liczba
jest parzystą liczbą całkowitą dodatnią, to liczba 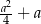 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.
Wykaż, że jeżeli 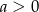 i
i 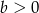 oraz
oraz 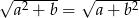 , to
, to 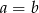 lub
lub 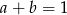 .
.
Wykaż, że jeżeli 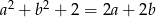 , to
, to 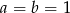 .
.
Wykaż, że jeśli 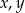 są liczbami różnymi od zera i
są liczbami różnymi od zera i 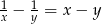 , to
, to 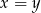 lub
lub 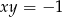 .
.
Wykaż, że dla 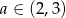 zachodzi równość
zachodzi równość 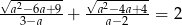 .
.
Udowodnij, że jeżeli 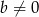 i
i 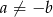 , to
, to 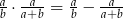 .
.
Wykaż, że jeśli 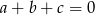 , to
, to 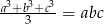 .
.
Uzasadnij, że jeśli 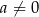 oraz
oraz 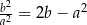 , to
, to 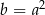 .
.
Uzasadnij, że jeśli 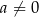 oraz
oraz 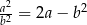 , to
, to 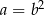 .
.
Uzasadnij, że jeśli 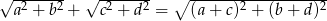 to
to 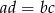 .
.
Wykaż, że jeśli 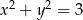 i
i 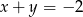 , to
, to 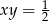 .
.
Wykaż, że jeśli 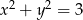 i
i 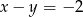 , to
, to 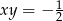 .
.
Udowodnij, że jeżeli liczba 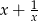 jest liczbą całkowitą, to liczba
jest liczbą całkowitą, to liczba 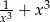 jest też liczbą całkowitą.
jest też liczbą całkowitą.
Udowodnij, że jeżeli liczby 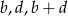 są różne od zera oraz
są różne od zera oraz 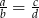 to
to 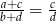 .
.
Udowodnij, że jeżeli liczby 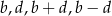 są różne od zera oraz
są różne od zera oraz 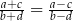 , to
, to 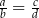 .
.
Udowodnij, że jeżeli liczby 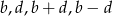 są różne od zera oraz
są różne od zera oraz 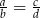 , to
, to 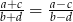 .
.
Suma dwóch liczb jest równa 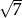 , a ich różnica jest równa
, a ich różnica jest równa 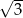 . Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
. Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
Uzasadnij, że jeżeli 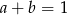 i
i 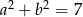 , to
, to 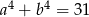 .
.
Uzasadnij, że jeżeli 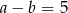 i
i 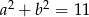 , to
, to 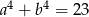 .
.
Wykaż, że jeżeli liczby rzeczywiste 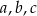 spełniają warunek
spełniają warunek  , to
, to