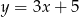Do wykresu funkcji 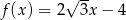 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 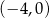 B)
B) 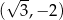 C)
C) 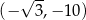 D)
D) 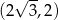
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Liniowy/Różne
Punkt 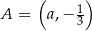 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 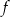 określonej wzorem
określonej wzorem 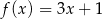 . Wynika stąd, że
. Wynika stąd, że
A) 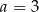 B)
B) 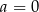 C)
C) 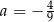 D)
D) 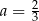
Wykres funkcji 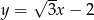 tworzy z osią
tworzy z osią 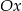 kąt rozwarty o mierze
kąt rozwarty o mierze
A) 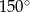 B)
B) 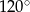 C)
C) 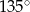 D)
D) 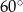
Wykres funkcji 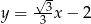 tworzy z osią
tworzy z osią 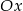 kąt rozwarty o mierze
kąt rozwarty o mierze
A) 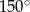 B)
B) 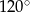 C)
C) 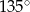 D)
D) 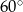
Gdy przesuniemy wykres funkcji 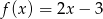 o 2 jednostki w prawo i 4 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 2 jednostki w prawo i 4 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 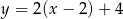 B)
B) 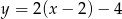 C)
C)  D)
D) 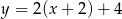
Gdy przesuniemy wykres funkcji 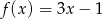 o 4 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 4 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 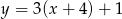 B)
B) 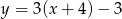 C)
C) 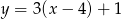 D)
D) 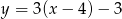
Punkt 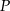 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 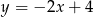 i
i 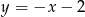 . Punkt
. Punkt 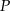 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) pierwszej B) drugiej C) trzeciej D) czwartej
Punkt 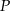 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 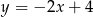 i
i 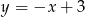 . Punkt
. Punkt 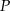 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) pierwszej B) drugiej C) trzeciej D) czwartej
Punkt 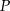 jest punktem przecięcia się wykresów funkcji
jest punktem przecięcia się wykresów funkcji 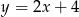 i
i 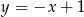 . Punkt
. Punkt 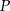 leży w układzie współrzędnych w ćwiartce
leży w układzie współrzędnych w ćwiartce
A) pierwszej B) drugiej C) trzeciej D) czwartej
Funkcja liniowa 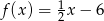
A) jest malejąca i jej wykres przechodzi przez punkt 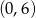
B) jest rosnąca i jej wykres przechodzi przez punkt 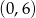
C) jest malejąca i jej wykres przechodzi przez punkt 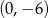
D) jest rosnąca i jej wykres przechodzi przez punkt 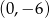
Funkcja liniowa 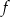 określona jest wzorem
określona jest wzorem 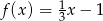 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Funkcja 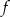 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś  w punkcie
w punkcie 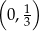
B) Funkcja 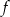 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś  w punkcie
w punkcie 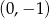
C) Funkcja 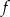 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 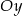 w punkcie
w punkcie 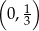
D) Funkcja 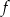 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 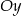 w punkcie
w punkcie 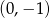
Funkcja liniowa 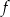 określona jest wzorem
określona jest wzorem 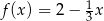 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Funkcja 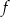 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 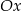 w punkcie
w punkcie 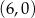
B) Funkcja 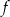 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 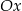 w punkcie
w punkcie 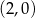
C) Funkcja 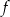 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 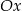 w punkcie
w punkcie 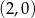
D) Funkcja 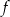 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 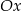 w punkcie
w punkcie 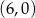
Wskaż funkcję, której wykres przecina prostą o równaniu 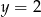 w punkcie o dodatnich współrzędnych.
w punkcie o dodatnich współrzędnych.
A) 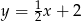 B)
B) 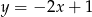 C)
C) 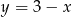 D)
D) 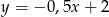
Wskaż funkcję, której wykres przecina prostą o równaniu 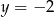 w punkcie o ujemnych współrzędnych.
w punkcie o ujemnych współrzędnych.
A) 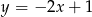 B)
B) 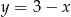 C)
C) 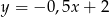 D)
D) 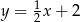
Gdy przesuniemy wykres funkcji 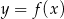 o 2 jednostki w prawo i o 3 jednostki w górę, to otrzymamy wykres funkcji
o 2 jednostki w prawo i o 3 jednostki w górę, to otrzymamy wykres funkcji 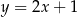 . Zatem
. Zatem
A) 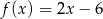 B)
B) 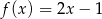 C)
C) 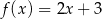 D)
D) 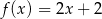
Gdy przesuniemy wykres funkcji 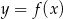 o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji
o 2 jednostki w lewo i o 3 jednostki w dół, to otrzymamy wykres funkcji 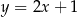 . Zatem
. Zatem
A) 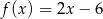 B)
B) 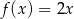 C)
C) 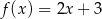 D)
D) 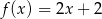
Wykres funkcji liniowej 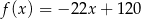 przechodzi przez ćwiartki układu współrzędnych:
przechodzi przez ćwiartki układu współrzędnych:
A) I, II, III B) I, II, IV C) I, III, IV D) II, III, IV
Wykres funkcji liniowej 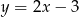 przecina oś
przecina oś 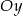 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 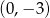 B)
B) 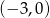 C)
C) 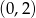 D)
D) 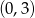
Wykres funkcji liniowej 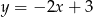 przecina oś
przecina oś 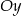 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 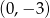 B)
B) 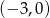 C)
C) 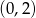 D)
D) 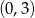
Funkcja liniowa 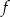 jest określona wzorem
jest określona wzorem 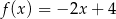 . Wykres funkcji
. Wykres funkcji 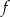 przesunięto wzdłuż osi
przesunięto wzdłuż osi 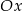 o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji
o 2 jednostki w lewo (tzn. przeciwnie do zwrotu osi), w wyniku czego otrzymano wykres funkcji 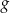 . Funkcja
. Funkcja 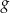 jest określona wzorem
jest określona wzorem
A) 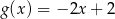 B)
B) 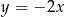 C)
C) 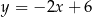 D)
D) 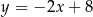
Funkcja liniowa 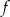 jest określona wzorem
jest określona wzorem 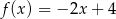 . Wykres funkcji
. Wykres funkcji 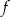 przesunięto wzdłuż osi
przesunięto wzdłuż osi 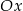 o 2 jednostki w prawo (tzn. zgodnie ze zwrotem osi), w wyniku czego otrzymano wykres funkcji
o 2 jednostki w prawo (tzn. zgodnie ze zwrotem osi), w wyniku czego otrzymano wykres funkcji 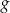 . Funkcja
. Funkcja 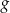 jest określona wzorem
jest określona wzorem
A) 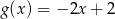 B)
B) 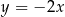 C)
C) 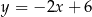 D)
D) 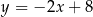
Wykres funkcji liniowej 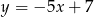 przecina pionową prostą przechodzącą przez punkt
przecina pionową prostą przechodzącą przez punkt 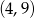 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 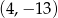 B)
B) 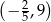 C)
C) 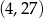 D)
D) 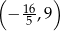
Wykres funkcji liniowej 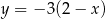 przecina prostą
przecina prostą 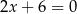 w punkcie
w punkcie
A) 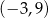 B)
B) 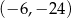 C)
C) 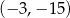 D)
D) 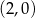
Punkt 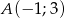 należy do wykresu funkcji:
należy do wykresu funkcji:
A) 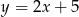 B)
B) 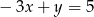 C)
C) 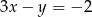 D)
D) 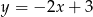
Do wykresu funkcji liniowej 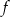 należą punkty
należą punkty 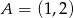 i
i 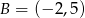 . Funkcja
. Funkcja 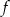 ma wzór
ma wzór
A) 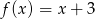 B)
B) 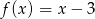 C)
C) 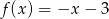 D)
D) 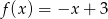
Do wykresu funkcji liniowej 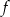 należą punkty
należą punkty 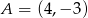 i
i 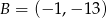 . Funkcja
. Funkcja 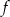 opisana jest wzorem
opisana jest wzorem
A) 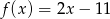 B)
B) 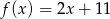 C)
C) 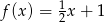 D)
D) 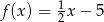
Przez punkty 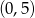 i
i 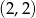 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 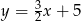 B)
B) 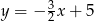 C)
C) 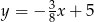 D)
D) 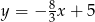
Do wykresu funkcji liniowej 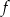 należą punkty
należą punkty 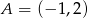 i
i 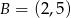 . Funkcja
. Funkcja 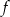 ma wzór
ma wzór
A) 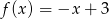 B)
B) 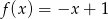 C)
C) 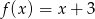 D)
D) 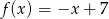
Do wykresu funkcji liniowej 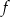 należą punkty
należą punkty 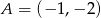 i
i 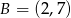 . Funkcja
. Funkcja 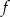 ma wzór
ma wzór
A) 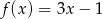 B)
B) 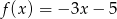 C)
C) 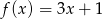 D)
D) 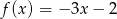
O funkcji liniowej 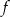 wiadomo, że
wiadomo, że 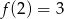 oraz punkt
oraz punkt 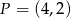 należy do jej wykresu. Wzór funkcji
należy do jej wykresu. Wzór funkcji 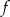 to
to
A) 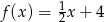 B)
B) 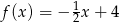 C)
C) 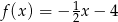 D)
D) 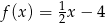
O funkcji liniowej 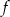 wiadomo, że
wiadomo, że 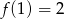 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 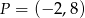 . Wzór funkcji
. Wzór funkcji 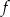 to
to
A) 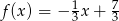 B)
B) 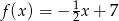 C)
C) 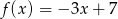 D)
D) 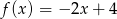
O funkcji liniowej 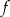 wiadomo, że
wiadomo, że 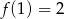 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 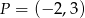 . Wzór funkcji
. Wzór funkcji 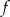 to
to
A) 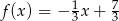 B)
B) 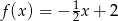 C)
C) 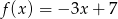 D)
D) 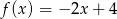
Przez punkty 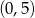 i
i 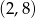 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 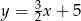 B)
B)  C)
C) 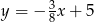 D)
D) 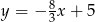
Przez punkty 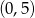 i
i 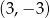 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 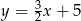 B)
B) 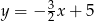 C)
C) 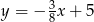 D)
D) 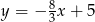
Do wykresu funkcji nie należy punkt 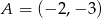 . Funkcja
. Funkcja 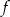 może mieć wzór
może mieć wzór
A) 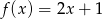 B)
B) 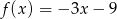 C)
C) 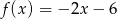 D)
D) 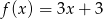
Gdy przesuniemy wykres funkcji 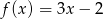 o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 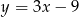 B)
B) 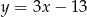 C)
C) 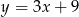 D)
D) 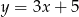
Aby otrzymać wykres funkcji 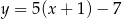 , należało wykres funkcji
, należało wykres funkcji 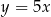 przesunąć
przesunąć
A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
C) o 1 jednostkę w prawo i 7 ku dołowi D) o 1 jednostkę w lewo i 7 ku górze
Gdy przesuniemy wykres funkcji 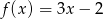 o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 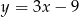 B)
B) 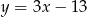 C)
C) 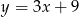 D)
D)