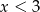Wiadomo, że 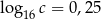 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
/Szkoła średnia/Zadania testowe/Liczby/Logarytmy/Z literkami/1 literka
Wiadomo, że 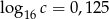 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
Jeśli 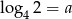 , to liczba
, to liczba  jest równa
jest równa
A) 16 B) 2 C) -2 D) 0,5
Jeżeli 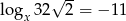 to liczba
to liczba  jest równa
jest równa
A) 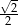 B)
B) 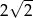 C)
C) 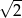 D) 2
D) 2
Jeżeli 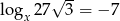 to liczba
to liczba  jest równa
jest równa
A) 3 B) 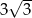 C)
C) 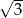 D)
D) 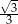
Liczba 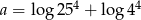 . Wynika stąd, że
. Wynika stąd, że
A) 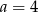 B)
B) 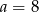 C)
C) 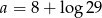 D)
D) 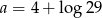
Liczba 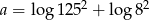 . Wynika stąd, że
. Wynika stąd, że
A) 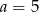 B)
B) 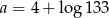 C)
C) 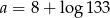 D)
D) 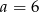
Liczba 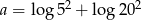 . Wynika stąd, że
. Wynika stąd, że
A) 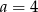 B)
B) 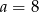 C)
C) 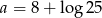 D)
D) 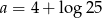
O liczbie  wiadomo, że
wiadomo, że 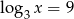 . Zatem
. Zatem
A) 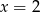 B)
B) 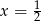 C)
C) 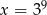 D)
D) 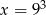
O liczbie  wiadomo, że
wiadomo, że 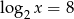 . Zatem
. Zatem
A) 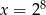 B)
B) 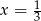 C)
C) 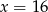 D)
D) 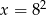
O liczbie  wiadomo, że
wiadomo, że 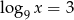 . Zatem
. Zatem
A) 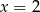 B)
B) 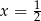 C)
C) 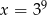 D)
D) 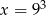
Jeśli 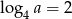 , to liczba
, to liczba  jest równa
jest równa
A) 16 B) 2 C) -2 D) 4
Jeżeli 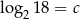 , to liczba
, to liczba 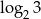 jest równa
jest równa
A) 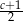 B)
B) 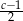 C)
C) 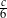 D)
D) 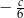
Jeżeli 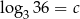 , to liczba
, to liczba 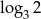 jest równa
jest równa
A) 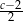 B)
B) 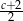 C)
C) 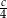 D)
D) 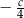
Jeżeli 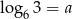 , to
, to 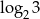 równa się
równa się
A) 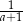 B)
B) 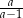 C)
C) 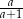 D)
D) 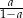
O liczbie dodatniej 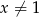 wiadomo, że
wiadomo, że 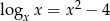 . Zatem
. Zatem
A) 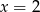 B)
B) 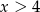 C)
C) 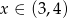 D)
D) 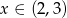
Liczba 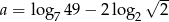 . Wynika z tego, że
. Wynika z tego, że
A) 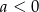 B)
B) 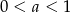 C)
C) 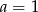 D)
D) 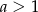
Liczba 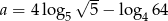 . Wynika z tego, że
. Wynika z tego, że
A) 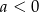 B)
B) 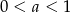 C)
C) 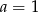 D)
D) 
Liczba 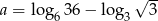 . Wynika z tego, że
. Wynika z tego, że
A) 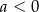 B)
B) 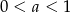 C)
C) 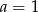 D)
D) 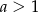
Liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 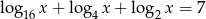 . Zatem
. Zatem
A) 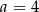 B)
B) 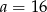 C)
C) 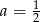 D)
D) 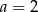
Jeżeli 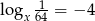 to liczba
to liczba  jest równa
jest równa
A) 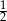 B)
B) 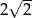 C) 2 D) 4
C) 2 D) 4
Jeżeli 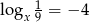 to liczba
to liczba  jest równa
jest równa
A) 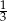 B) 3 C)
B) 3 C) 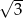 D)
D) 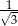
Jeżeli 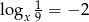 to liczba
to liczba  jest równa
jest równa
A) 3 B) 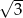 C)
C) 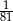 D) 81
D) 81
Jeśli 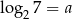 , to liczba
, to liczba 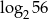 jest równa
jest równa
A) 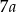 B)
B) 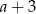 C)
C) 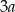 D)
D) 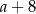
Jeżeli 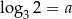 , to liczba
, to liczba 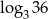 jest równa
jest równa
A) 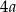 B)
B) 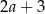 C)
C) 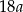 D)
D) 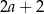
Niech 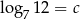 . Wtedy
. Wtedy 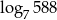 jest równy
jest równy
A) 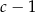 B)
B)  C)
C) 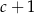 D)
D) 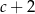
Wiedząc, że 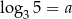 , określ wartość wyrażenia
, określ wartość wyrażenia 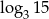 jest równa
jest równa
A) 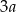 B)
B) 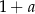 C)
C) 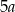 D)
D) 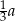
Niech 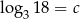 . Wtedy
. Wtedy 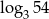 jest równy
jest równy
A) 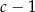 B)
B)  C)
C) 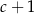 D)
D) 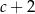
Jeśli 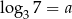 , to liczba
, to liczba 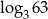 jest równa
jest równa
A) 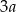 B)
B) 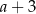 C)
C) 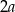 D)
D) 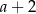
Jeśli 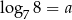 , to liczba
, to liczba 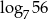 jest równa
jest równa
A) 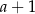 B)
B) 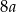 C)
C) 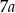 D)
D) 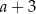
Jeśli 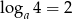 , to liczba
, to liczba  jest równa
jest równa
A) 16 B) 2 C) -2 D) 4
Wyrażenie 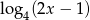 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 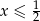 B)
B) 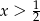 C)
C) 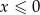 D)
D) 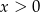
Wyrażenie 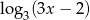 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 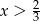 B)
B) 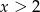 C)
C) 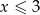 D)
D) 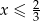
Jeżeli 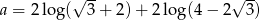 to
to 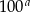 jest liczbą
jest liczbą
A) ujemną B) nieparzystą C) niewymierną D) parzystą
Jeżeli 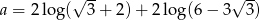 to
to 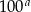 jest liczbą
jest liczbą
A) ujemną B) nieparzystą C) niewymierną D) parzystą
Równość 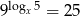 jest prawdziwa dla
jest prawdziwa dla
A) 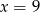 B)
B) 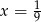 C)
C) 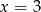 D)
D) 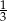
Wyrażenie 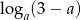 ma sens liczbowy dla każdej liczby
ma sens liczbowy dla każdej liczby  należącej do zbioru
należącej do zbioru
A) 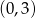 B)
B) 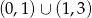 C)
C) 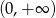 D)
D) 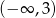
Wyrażenie 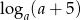 ma sens liczbowy dla każdej liczby
ma sens liczbowy dla każdej liczby  należącej do zbioru
należącej do zbioru
A) 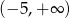 B)
B) 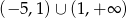 C)
C) 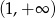 D)
D) 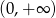
Jeżeli 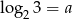 to wyrażenie
to wyrażenie 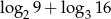 jest równe
jest równe
A) 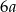 B)
B) 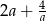 C)
C) 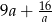 D)
D) 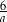
Jeżeli 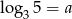 to wyrażenie
to wyrażenie 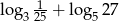 jest równe
jest równe
A)  B)
B) 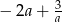 C)
C) 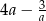 D)
D) 
Liczba 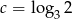 . Wtedy
. Wtedy
A) 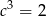 B)
B) 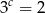 C)
C) 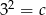 D)
D) 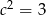
Liczba 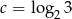 . Wtedy
. Wtedy
A) 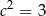 B)
B) 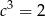 C)
C) 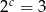 D)
D) 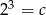
Rozwiązaniem równania 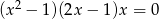 nie jest liczba
nie jest liczba
A) 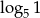 B)
B) 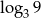 C)
C) 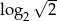 D)
D) 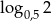
Rozwiązaniem równania 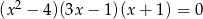 nie jest liczba
nie jest liczba
A) 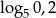 B)
B) 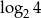 C)
C) 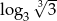 D)
D) 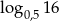
Wyrażenie 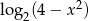 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 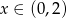 B)
B) 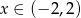 C)
C) 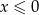 D)
D) 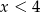
Wyrażenie 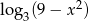 jest określone dla wszystkich liczb
jest określone dla wszystkich liczb  spełniających warunek
spełniających warunek
A) 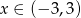 B)
B) 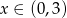 C)
C) 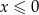 D)
D)