W dwóch hotelach wybudowano prostokątne baseny. Basen w pierwszym hotelu ma powierzchnię 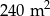 . Basen w drugim hotelu ma powierzchnię
. Basen w drugim hotelu ma powierzchnię 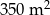 oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
oraz jest o 5 m dłuższy i 2 m szerszy niż w pierwszym hotelu. Oblicz, jakie wymiary mogą mieć baseny w obu hotelach. Podaj wszystkie możliwe odpowiedzi.
/Szkoła średnia/Zadania z treścią/Geometryczne/Długość i odległość
Dwie szkoły wybudowały boiska do piłki nożnej. Powierzchnia pierwszego ma 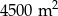 . Drugie boisko jest o 10 metrów szersze oraz 20 metrów dłuższe od pierwszego i ma powierzchnię
. Drugie boisko jest o 10 metrów szersze oraz 20 metrów dłuższe od pierwszego i ma powierzchnię 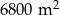 . Podaj wymiary obu boisk szkolnych. Uwzględnij wymaganie, że boisko piłkarskie musi mieć kształt prostokąta, ale nie może być kwadratem. Długość boiska do piłki nożnej nie może przekraczać 120 metrów ani być mniejsza niż 70 metrów. Musi też być w każdym przypadku dłuższa od szerokości boiska, która ma mieścić się w przedziale od 45 m do 90 m.
. Podaj wymiary obu boisk szkolnych. Uwzględnij wymaganie, że boisko piłkarskie musi mieć kształt prostokąta, ale nie może być kwadratem. Długość boiska do piłki nożnej nie może przekraczać 120 metrów ani być mniejsza niż 70 metrów. Musi też być w każdym przypadku dłuższa od szerokości boiska, która ma mieścić się w przedziale od 45 m do 90 m.
W dwóch szkołach wybudowano prostokątne baseny. W pierwszej z nich powierzchnia basenu wynosi 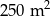 , w drugiej zaś jest o
, w drugiej zaś jest o 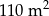 większa, a boki prostokąta odpowiednio dłuższe o 2 m na szerokości i o 5 m na długości basenu. Oblicz wymiary basenów w obu szkołach.
większa, a boki prostokąta odpowiednio dłuższe o 2 m na szerokości i o 5 m na długości basenu. Oblicz wymiary basenów w obu szkołach.
Dane są dwie prostokątne działki. Działka pierwsza ma powierzchnię równą 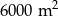 . Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o
. Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o 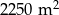 . Oblicz wymiary pierwszej działki.
. Oblicz wymiary pierwszej działki.
Dwie prostokątne działki ogrodnicze mają odpowiednio pola powierzchni 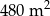 i
i 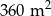 . Druga z działek jest o 2 metry węższa i o 4 metry krótsza od pierwszej działki. Oblicz, jakie wymiary mogą mieć działki. Podaj wszystkie możliwe odpowiedzi.
. Druga z działek jest o 2 metry węższa i o 4 metry krótsza od pierwszej działki. Oblicz, jakie wymiary mogą mieć działki. Podaj wszystkie możliwe odpowiedzi.
Prostokątne zdjęcie o szerokości 30 cm i długości 45 cm oprawiono w prostokątną ramkę o jednakowej szerokości. Jaka jest szerokość ramki, jeśli pole zdjęcia wraz z ramką wynosi 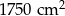 ?
?
Prostokątne zdjęcie o szerokości 15 cm i długości 20 cm oprawiono w prostokątną ramkę o jednakowej szerokości. Jaka jest szerokość ramki, jeśli pole zdjęcia wraz z ramką wynosi 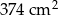 ?
?
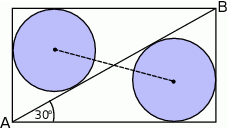
Na rysunku przedstawiony został szkic części parku. Dwie fontanny wpisano w prostokątny klomb kwiatów. Są one styczne do linii przekątnej klombu. Wiedząc, że przekątna klombu ma długość 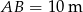 oraz tworzy ona z jednym z boków klombu kąt o mierze
oraz tworzy ona z jednym z boków klombu kąt o mierze 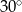 , wyznacz odległość środków tych fontann.
, wyznacz odległość środków tych fontann.
Pole każdej z dwóch prostokątnych działek jest równe 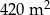 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.
Pole każdej z dwóch prostokątnych działek jest równe 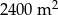 . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.
. Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.
W architekturze islamu często stosowanym elementem był łuk podkowiasty. Schemat okna w kształcie takiego łuku (łuku okręgu) przedstawiono na rysunku poniżej. Korzystając z danych na rysunku oblicz wysokość okna 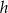 i największy prześwit
i największy prześwit 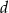 .
.
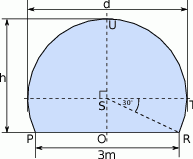
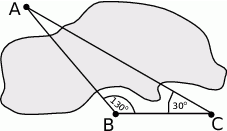
Obiekty 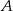 i
i 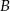 leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektami
leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektami 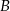 i
i 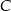 jest równa 400 m. Oblicz odległość w linii prostej między obiektami
jest równa 400 m. Oblicz odległość w linii prostej między obiektami 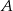 i
i 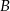 i podaj wynik, zaokrąglając go do jednego metra.
i podaj wynik, zaokrąglając go do jednego metra.
W wyniku tzw. złotego podziału odcinka otrzymuje się dwa nowe odcinki o tej własności, że stosunek krótszego z nich do dłuższego jest równy stosunkowi dłuższego z nich do całego odcinka. Dokonano złotego podziału odcinka o długości 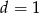 , oblicz długość krótszej części.
, oblicz długość krótszej części.
Metalowy stożek, którego tworząca o długości 10 jest nachylona do płaszczyzny podstawy pod kątem 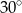 , przetopiono na sześć jednakowych kulek. Oblicz promień kulki.
, przetopiono na sześć jednakowych kulek. Oblicz promień kulki.
Z metalowej rury wycięto dwa walce o tym samym promieniu podstawy. Objętość pierwszego z walców jest równa 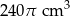 , a drugi walec jest wyższy od pierwszego o
, a drugi walec jest wyższy od pierwszego o 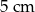 i ma objętość większą o
i ma objętość większą o 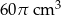 . Oblicz wysokości obu walców.
. Oblicz wysokości obu walców.
Dwie szkoły mają prostokątne boiska. Przekątna każdego boiska jest równa 65 m. Boisko w drugiej szkole ma długość o 4 m większą niż boisko w pierwszej szkole, ale szerokość o 8 m mniejszą. Oblicz długość i szerokość każdego z tych boisk.
Z dwóch okrągłych kawałków blachy o średnicy 25 cm wycięto dwa prostokąty w ten sposób, że wierzchołki prostokątów znajdowały się na brzegu kół (patrz rysunek).
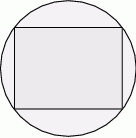
Pierwszy prostokąt miał długość o 4 cm większą niż drugi prostokąt, ale szerokość o 8 cm mniejszą. Oblicz długość i szerokość każdego z prostokątów.
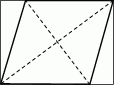
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?
Przed wejściem do przychodni lekarskiej znajdują się schody mające 8 stopni po 15 cm wysokości każdy. Obok schodów jest podjazd dla niepełnosprawnych o nachyleniu 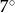 . Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm. (
. Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm. (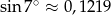 )
)
Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą 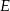 . Z punktu
. Z punktu 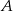 widziała ją pod kątem
widziała ją pod kątem 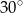 stopni do kierunku drogi. A z punktu
stopni do kierunku drogi. A z punktu 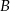 pod kątem
pod kątem 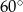 . Przejeżdżając przez punkt
. Przejeżdżając przez punkt 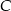 minęła elektrownię. Długość odcinka
minęła elektrownię. Długość odcinka 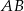 jest równa 20km.
jest równa 20km.
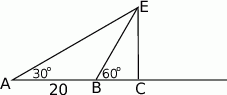
- Oblicz miary kątów
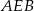 i
i 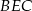 .
. - Oblicz długość odcinka
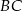 .
. - Oblicz odległość elektrowni od drogi.
W rachunkach przyjmij, że 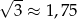 .
.
Dziesięć kul bilardowych średnicy 6 cm umieszczono w prostokątnym pudełku tak jako pokazano to na rysunku.
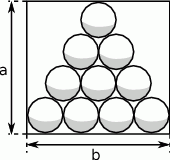
Wyznacz wymiary  i
i 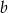 tego pudełka.
tego pudełka.
Oblicz szerokość prostokątnej ramy obrazu wiedząc, że obwód zewnętrzny ramy jest o 28 cm większy od obwodu wewnętrznego tej ramy.

