Wyznacz równania prostych stycznych do okręgu o równaniu 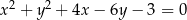 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 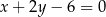 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczne do okręgu
Wyznacz równania prostych stycznych do okręgu o równaniu 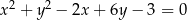 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 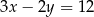 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 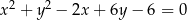 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 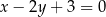 .
.
Znajdź równania stycznych do okręgu 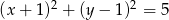 poprowadzonych z punktu
poprowadzonych z punktu 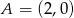 .
.
Znajdź równania stycznych do okręgu 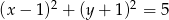 poprowadzonych z punktu
poprowadzonych z punktu 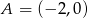 .
.
Wyznacz równania stycznych do okręgu 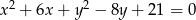 równoległych do osi
równoległych do osi 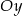 .
.
Wyznacz równania stycznych do okręgu o równaniu 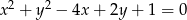 , równoległych do osi odciętych układu współrzędnych.
, równoległych do osi odciętych układu współrzędnych.
Wyznacz równania stycznych do okręgu o równaniu 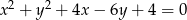 , równoległych do osi rzędnych układu współrzędnych.
, równoległych do osi rzędnych układu współrzędnych.
Dany jest okrąg o równaniu 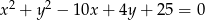 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
. Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
Wyznacz równania stycznych do okręgu 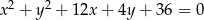 , przechodzących przez początek układu współrzędnych.
, przechodzących przez początek układu współrzędnych.
Wykaż, że styczne do okręgu 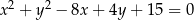 poprowadzone przez punkt
poprowadzone przez punkt 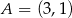 są prostopadłe.
są prostopadłe.
Okrąg 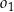 o równaniu
o równaniu 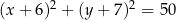 oraz okrąg
oraz okrąg 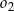 o środku
o środku 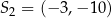 są wewnętrznie styczne, przy czym okrąg
są wewnętrznie styczne, przy czym okrąg 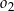 zawiera się w kole opisanym nierównością
zawiera się w kole opisanym nierównością 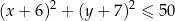 . Napisz równanie wspólnej stycznej do obu okręgów.
. Napisz równanie wspólnej stycznej do obu okręgów.
Styczne do okręgu o równaniu 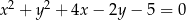 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 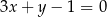 , przecinają prostą
, przecinają prostą 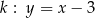 w punktach
w punktach 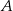 i
i 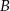 . Oblicz pole trójkąta
. Oblicz pole trójkąta 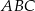 , jeśli
, jeśli 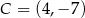 .
.
Okrąg o środku 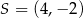 przechodzi przez punkt
przechodzi przez punkt 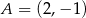 . Napisz równanie stycznej do tego okręgu przechodzącej przez punkt
. Napisz równanie stycznej do tego okręgu przechodzącej przez punkt 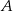 .
.
Oblicz miarę kąta między stycznymi do okręgu  poprowadzonymi przez punkt
poprowadzonymi przez punkt 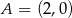 .
.
Oblicz miarę kąta między stycznymi do okręgu 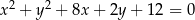 poprowadzonymi przez punkt
poprowadzonymi przez punkt 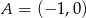 .
.
Wyznacz równanie prostej prostopadłej do wektora ![→ u = [0,− 3]](https://img.zadania.info/zad/6101909/HzadT0x.gif) i stycznej do okręgu
i stycznej do okręgu 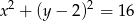 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 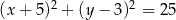 równoległych do prostej o równaniu
równoległych do prostej o równaniu 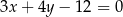 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 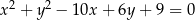 równoległych do prostej o równaniu
równoległych do prostej o równaniu 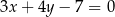 .
.
Znajdź równania prostych stycznych do dwóch okręgów: 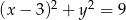 i
i 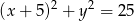 .
.
Dany jest okrąg o równaniu 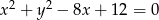 .
.
- Wyznacz równania stycznych do okręgu przechodzących przez początek układu współrzędnych.
- Oblicz pole figury ograniczonej stycznymi i łukiem okręgu wyznaczonym przez punkty styczności.
Z punktu 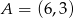 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 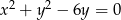 .
.
- Wyznacz równania tych stycznych.
- Oblicz odległość punktów styczności.
- Oblicz pole figury zaznaczonej na rysunku.
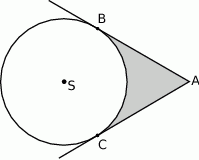
Dany jest okrąg o równaniu 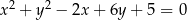 .
.
- Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu
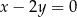 .
. - Oblicz pole trójkąta
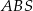 , gdzie
, gdzie 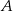 i
i 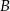 są punktami przecięcia się stycznych z prostą o równaniu
są punktami przecięcia się stycznych z prostą o równaniu 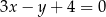 , zaś
, zaś 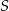 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Z punktu 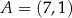 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 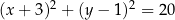 . Oblicz pole trójkąta
. Oblicz pole trójkąta 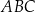 , gdzie
, gdzie 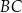 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Z punktu 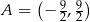 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 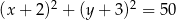 . Oblicz pole trójkąta
. Oblicz pole trójkąta 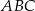 , gdzie
, gdzie 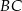 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Wyznacz równanie prostych przechodzących przez początek układu współrzędnych i stycznych do okręgu o środku w punkcie 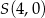 i promieniu
i promieniu 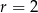 .
.
W układzie współrzędnych narysuj okrąg o równaniu 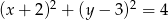 oraz zaznacz punkt
oraz zaznacz punkt 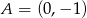 . Prosta o równaniu
. Prosta o równaniu 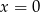 jest jedną ze stycznych do tego okręgu przechodzących przez punkt
jest jedną ze stycznych do tego okręgu przechodzących przez punkt 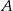 . Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt
. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt 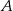 .
.
W kartezjańskim układzie współrzędnych 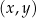 środek
środek 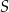 okręgu o promieniu
okręgu o promieniu 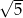 leży na prostej o równaniu
leży na prostej o równaniu 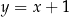 . Przez punkt
. Przez punkt 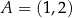 , którego odległość od punktu
, którego odległość od punktu 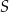 jest większa od
jest większa od 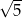 , poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio –
, poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio – 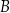 i
i 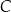 . Pole czworokąta
. Pole czworokąta 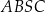 jest równe 15. Oblicz współrzędne punktu
jest równe 15. Oblicz współrzędne punktu 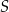 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.

