W nieskończonym ciągu geometrycznym 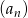 o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.
/Szkoła średnia/Ciągi/Geometryczny/Różne
Różnica między pierwszym a siódmym wyrazem ciągu geometrycznego jest równa 63, a różnica między wyrazem pierwszym a czwartym jest równa 72. Oblicz sumę pierwszych 7 wyrazów tego ciągu.
Ciąg 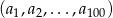 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 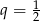 i pierwszym wyrazie równym
i pierwszym wyrazie równym 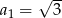 . Oblicz sumę
. Oblicz sumę
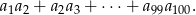
Pierwszy wyraz niemonotonicznego ciągu geometrycznego 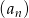 jest równy 48 i jest o 36 większy od wyrazu trzeciego.
jest równy 48 i jest o 36 większy od wyrazu trzeciego.
- Oblicz iloraz ciągu
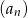 .
. - Oblicz ósmy wyraz ciągu
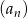 .
. - Suma kilku początkowych wyrazów ciągu
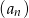 jest równa
jest równa 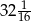 . Oblicz, ile wyrazów zsumowano.
. Oblicz, ile wyrazów zsumowano.
Sprawdź, czy ciąg o wyrazach 2, 6, 18, 36 jest geometryczny.
Oblicz 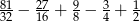 . Wynik podaj w postaci ułamka nieskracalnego.
. Wynik podaj w postaci ułamka nieskracalnego.
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 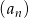 , w którym
, w którym 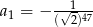 oraz
oraz 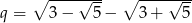 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Ciąg geometryczny 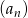 jest określony wzorem
jest określony wzorem 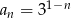 dla
dla 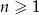 .
.
- Oblicz iloraz tego ciągu.
- Oblicz
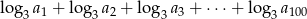 czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
czyli sumę logarytmów, o podstawie 3, stu początkowych, kolejnych wyrazów tego ciągu.
Ciąg 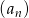 , dla
, dla 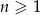 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 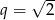 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
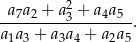
Oblicz sumę 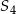 pierwszych 4 wyrazów ciągu geometrycznego
pierwszych 4 wyrazów ciągu geometrycznego 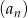 , o pierwszym wyrazie
, o pierwszym wyrazie 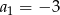 i ilorazie
i ilorazie 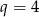 .
.
Dwudziestowyrazowy ciąg geometryczny 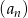 określony jest wzorem
określony jest wzorem 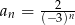 dla
dla 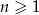 . Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Oblicz sumę ośmiu początkowych wyrazów rosnącego ciągu geometrycznego, w którym 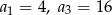 .
.
Oblicz sumę siedmiu początkowych wyrazów ciągu geometrycznego 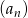 , w którym
, w którym 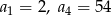 .
.
Oblicz sumę dziewięciu początkowych wyrazów rosnącego ciągu geometrycznego 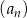 , określonego dla
, określonego dla 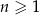 , w którym
, w którym 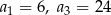 .
.
Wszystkie wyrazy ciągu geometrycznego 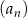 , określonego dla
, określonego dla 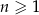 , są dodatnie. Wyrazy tego ciągu spełniają warunek
, są dodatnie. Wyrazy tego ciągu spełniają warunek 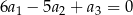 . Oblicz iloraz
. Oblicz iloraz 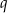 tego ciągu należący do przedziału
tego ciągu należący do przedziału 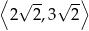 .
.
Wszystkie wyrazy ciągu geometrycznego 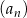 , określonego dla
, określonego dla 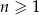 , są dodatnie. Wyrazy tego ciągu spełniają warunek
, są dodatnie. Wyrazy tego ciągu spełniają warunek 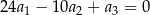 . Oblicz iloraz
. Oblicz iloraz 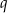 tego ciągu należący do przedziału
tego ciągu należący do przedziału 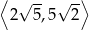 .
.
Wyrazy niezerowego ciągu geometrycznego 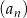 , określonego dla
, określonego dla 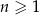 spełniają warunki:
spełniają warunki: 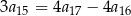 oraz
oraz 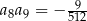 . Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.
. Oblicz iloczyn pierwszych sześciu wyrazów tego ciągu.
Oblicz pierwszy wyraz i iloraz ciągu geometrycznego wiedząc, że trzeci wyraz jest równy 18, a szósty 486.
Ciąg 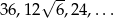 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
- Oblicz iloraz
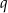 tego ciągu.
tego ciągu. - Zapisz
 -ty wyraz tego ciągu w postaci
-ty wyraz tego ciągu w postaci 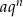
- Oblicz sumę ośmiu początkowych wyrazów tego ciągu.
Wyznacz wzór ogólny ciągu geometrycznego wiedząc, że 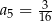 oraz
oraz 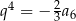 .
.
Dany jest ciąg geometryczny, w którym 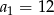 i
i 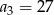 .
.
- Ile jest ciągów spełniających podane warunki? Odpowiedź uzasadnij.
- Oblicz wyraz
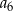 tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
Kolejne cyfry dodatniej liczby trzycyfrowej tworzą ciąg geometryczny. Suma cyfr jedności i dziesiątek jest o jeden większa od cyfry setek. Jeżeli od szukanej liczby odejmiemy liczbę złożoną z tych samych cyfr, lecz napisanych w odwrotnej kolejności to otrzymamy 495. Znajdź tę liczbę.
Pierwszy wyraz i iloraz nieskończonego ciągu geometrycznego malejącego 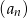 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 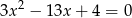 . Sprawdź czy prawdziwa jest nierówność
. Sprawdź czy prawdziwa jest nierówność 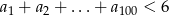 .
.

