Punkty 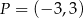 ,
, 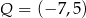 i
i 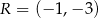 są środkami odpowiednio boków
są środkami odpowiednio boków 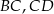 i
i 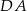 równoległoboku
równoległoboku 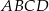 . Wyznacz współrzędne wierzchołków tego równoległoboku.
. Wyznacz współrzędne wierzchołków tego równoległoboku.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Równoległobok
W kartezjańskim układzie współrzędnych 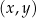 dany jest równoległobok
dany jest równoległobok 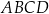 , w którym
, w którym 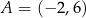 oraz
oraz 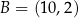 . Przekątne
. Przekątne 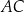 oraz
oraz 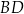 tego równoległoboku przecinają się w punkcie
tego równoległoboku przecinają się w punkcie 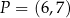 . Oblicz długość boku
. Oblicz długość boku 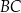 tego równoległoboku.
tego równoległoboku.
Dany jest równoległobok 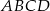 o wierzchołkach
o wierzchołkach 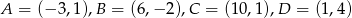 . Napisz równania prostych, w których zawarte są przekątne równoległoboku.
. Napisz równania prostych, w których zawarte są przekątne równoległoboku.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 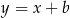 ,
, 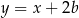 ,
, 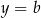 ,
, 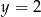 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 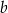 spełnia warunki:
spełnia warunki: 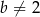 i
i 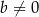 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 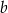 , dla których pole tego równoległoboku jest równe 1.
, dla których pole tego równoległoboku jest równe 1.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 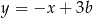 ,
, 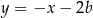 ,
, 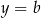 ,
, 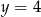 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 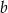 spełnia warunki:
spełnia warunki: 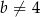 i
i 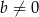 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 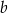 , dla których pole tego równoległoboku jest równe 20.
, dla których pole tego równoległoboku jest równe 20.
W kartezjańskim układzie współrzędnych 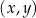 przekątne równoległoboku
przekątne równoległoboku 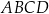 przecinają się w punkcie
przecinają się w punkcie 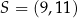 . Bok
. Bok 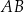 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 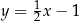 , a bok
, a bok 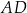 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 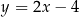 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 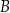 oraz długość odcinka
oraz długość odcinka 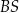 .
.
Boki 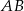 i
i 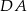 równoległoboku
równoległoboku 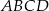 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 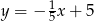 i
i 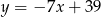 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 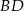 tego równoległoboku, jeżeli jego środek ma współrzędne
tego równoległoboku, jeżeli jego środek ma współrzędne 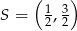 .
.
Punkty 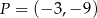 ,
, 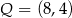 i
i 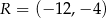 są środkami odpowiednio boków
są środkami odpowiednio boków 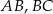 i
i 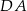 równoległoboku
równoległoboku 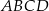 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 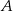 tego równoległoboku.
tego równoległoboku.
W kartezjańskim układzie współrzędnych 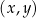 przekątne równoległoboku
przekątne równoległoboku 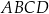 przecinają się w punkcie
przecinają się w punkcie 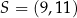 . Bok
. Bok 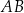 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 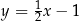 , a bok
, a bok 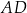 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 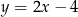 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 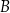 .
.
W kartezjańskim układzie współrzędnych 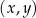 przekątne równoległoboku
przekątne równoległoboku 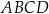 przecinają się w punkcie
przecinają się w punkcie 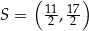 . Bok
. Bok 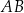 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 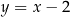 , a bok
, a bok 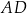 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 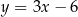 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 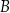 .
.
Punkty 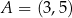 ,
, 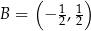 ,
, 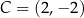 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 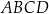 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 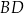 tego równoległoboku.
tego równoległoboku.
Sprawdź, czy czworokąt  , gdzie
, gdzie 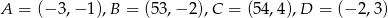 jest równoległobokiem. Odpowiedź uzasadnij.
jest równoległobokiem. Odpowiedź uzasadnij.
Punkt 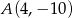 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku  . Dwa boki równoległoboku zawierają się w prostych o równaniach
. Dwa boki równoległoboku zawierają się w prostych o równaniach 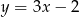 i
i 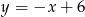 . Wyznacz pozostałe wierzchołki równoległoboku.
. Wyznacz pozostałe wierzchołki równoległoboku.
Dane są równania prostych 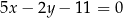 i
i 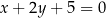 , w których zawierają się dwa boki równoległoboku. Punkt
, w których zawierają się dwa boki równoległoboku. Punkt 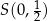 jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 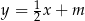 ,
, 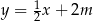 ,
, 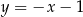 ,
, 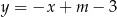 , gdzie
, gdzie 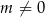 i
i 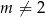 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 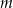 , dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy
, dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy 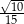 .
.
Punkty 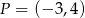 ,
, 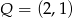 i
i 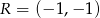 są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
Punkty 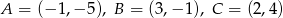 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 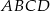 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Oblicz pole równoległoboku 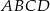 o wierzchołkach
o wierzchołkach 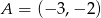 ,
, 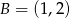 ,
, 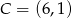 ,
, 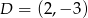 .
.
W równoległoboku 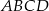 dane są wierzchołki
dane są wierzchołki 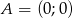 ,
, 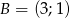 ,
, 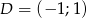 . Wyznacz wierzchołek
. Wyznacz wierzchołek 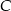 oraz środek symetrii tego równoległoboku.
oraz środek symetrii tego równoległoboku.
Wyznacz współrzędne wierzchołka 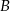 równoległoboku
równoległoboku 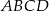 jeżeli
jeżeli 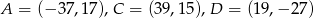 .
.
Pole równoległoboku 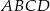 o danych wierzchołkach
o danych wierzchołkach 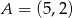 i
i 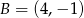 jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej
jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 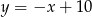 , który ma obie współrzędne będące liczbami całkowitymi.
, który ma obie współrzędne będące liczbami całkowitymi.

