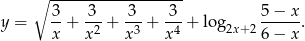Wiedząc, że zbiorem wartości funkcji 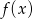 jest przedział
jest przedział 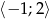 wyznacz wszystkie wartości
wyznacz wszystkie wartości 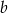 , dla których funkcja
, dla których funkcja 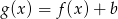 nie ma miejsc zerowych.
nie ma miejsc zerowych.
/Szkoła średnia/Funkcje/Różne
Liczba  jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 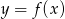 . Wyznacz miejsca zerowe funkcji:
. Wyznacz miejsca zerowe funkcji: 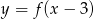 .
.
Liczba  jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 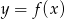 . Wyznacz miejsca zerowe funkcji:
. Wyznacz miejsca zerowe funkcji: 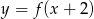 .
.
Liczba  jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 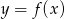 . Wyznacz miejsca zerowe funkcji
. Wyznacz miejsca zerowe funkcji 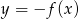 .
.
Liczba  jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 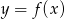 . Wyznacz miejsca zerowe funkcji
. Wyznacz miejsca zerowe funkcji 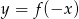 .
.
Oblicz granicę jednostronną 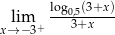 .
.
Funkcja 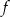 ma następujące własności:
ma następujące własności:
1. Dziedziną funkcji jest przedział 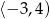 .
.
2. Przedział 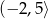 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji 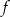 .
.
3. Funkcja ma dwa miejsca zerowe -2 oraz 3.
4. Funkcja 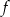 jest rosnąca w przedziale
jest rosnąca w przedziale 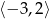 i malejąca w przedziale
i malejąca w przedziale 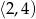 . Podaj zbiór rozwiązań nierówności
. Podaj zbiór rozwiązań nierówności 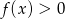 .
.
Wyznaczyć dziedzinę funkcji 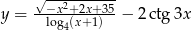 .
.
Oblicz granicę funkcji 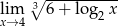 .
.
Oblicz wartość funkcji 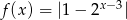 dla argumentu
dla argumentu
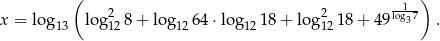
Oblicz wartość funkcji 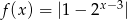 dla argumentu
dla argumentu 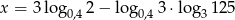 .
.
Z trzech prostopadłościennych belek 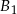 ,
, 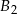 ,
, 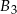 o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1 m, 2 m, 1 m sklejono jedną belkę o długości 4 m. Każda z belek
o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1 m, 2 m, 1 m sklejono jedną belkę o długości 4 m. Każda z belek 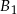 ,
, 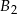 ,
, 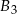 wykonana jest z innego materiału, a ich masy są równe odpowiednio 20 kg, 30 kg, 10 kg.
wykonana jest z innego materiału, a ich masy są równe odpowiednio 20 kg, 30 kg, 10 kg.
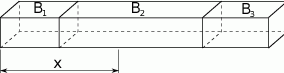
Masa odcinka belki o długosci  jest funkcją zmiennej
jest funkcją zmiennej  . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
Z równania 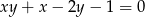 wyznacz
wyznacz 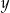 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.
. Wyznacz jej dziedzinę oraz współrzędne punktów przecięcia wykresu z osiami układu współrzędnych.
Wyznacz dziedzinę i zbiór wartości funkcji
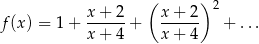
Naszkicuj wykres funkcji 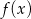 .
.
Oblicz granicę 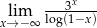 .
.
Oblicz granicę 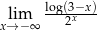 .
.
Wyznacz dziedzinę funkcji