Liczby 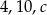 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Równoramienny/Oblicz długość...
Liczby 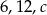 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 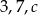 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
W trójkącie równoramiennym wysokość poprowadzona do podstawy ma długość 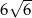 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
. Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
W trójkącie 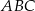 boki
boki 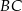 i
i 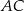 są równej długości. Prosta
są równej długości. Prosta 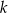 jest prostopadła do podstawy
jest prostopadła do podstawy 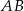 tego trójkąta i przecina boki
tego trójkąta i przecina boki 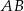 oraz
oraz 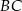 w punktach – odpowiednio –
w punktach – odpowiednio – 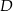 i
i 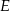 . Pole czworokąta
. Pole czworokąta 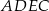 jest 17 razy większe od pola trójkąta
jest 17 razy większe od pola trójkąta 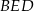 . Oblicz
. Oblicz 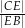 .
.
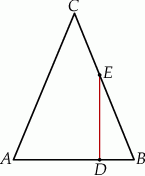
W trójkącie 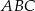 boki
boki 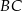 i
i 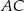 są równej długości. Prosta
są równej długości. Prosta 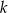 jest prostopadła do podstawy
jest prostopadła do podstawy 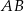 tego trójkąta i przecina boki
tego trójkąta i przecina boki 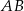 oraz
oraz 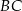 w punktach – odpowiednio –
w punktach – odpowiednio – 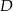 i
i 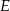 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 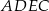 do pola trójkąta
do pola trójkąta 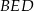 jeżeli
jeżeli 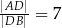 .
.
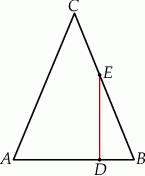
Podstawa 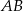 trójkąta równoramiennego
trójkąta równoramiennego 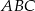 ma długość 8 oraz
ma długość 8 oraz 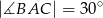 . Oblicz długość środkowej
. Oblicz długość środkowej 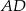 tego trójkąta.
tego trójkąta.
W trójkącie równoramiennym 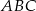 (
(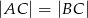 ) miara kąta
) miara kąta 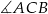 jest równa
jest równa 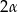 . Promień okręgu wpisanego w ten trójkąt ma długość
. Promień okręgu wpisanego w ten trójkąt ma długość  . Oblicz długości boków trójkąta
. Oblicz długości boków trójkąta 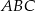 .
.
W trójkącie równoramiennym podstawa ma długość 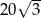 . Pole trójkąta jest równe
. Pole trójkąta jest równe 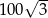 . Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
. Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Liczby 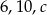 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Podstawa trójkąta równoramiennego i środkowe poprowadzone z jej konców mają długość  . Oblicz długość wysokości poprowadzonej do podstawy.
. Oblicz długość wysokości poprowadzonej do podstawy.
Na trójkącie równoramiennym 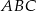 (
(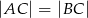 ) o polu równym
) o polu równym 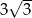 opisano okrąg, którego promień ma długość 2 cm. Oblicz długość wysokości
opisano okrąg, którego promień ma długość 2 cm. Oblicz długość wysokości 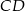 tego trójkąta.
tego trójkąta.
Na okręgu o promieniu 9 opisano trójkąt równoramienny o kącie równym 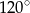 . Oblicz długości boków trójkąta.
. Oblicz długości boków trójkąta.
W ostrokątnym trójkącie równoramiennym ramię ma długość 61, a wysokość poprowadzona do ramienia ma długość 11. Oblicz długość podstawy tego trójkąta.
W trójkącie 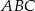 dane są długości boków
dane są długości boków 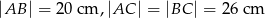 . Wyznacz długość środkowej
. Wyznacz długość środkowej 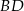 .
.
W trójkąt równoramienny 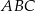 o podstawie długości
o podstawie długości 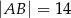 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek
i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek 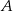 z punktem wspólnym okręgu i ramienia
z punktem wspólnym okręgu i ramienia 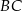 .
.
Podstawa trójkąta równoramiennego ma długość 4. Środek okręgu opisanego na tym trójkącie dzieli jedną z wysokości trójkąta na odcinki, których stosunek długości wynosi 3:5. Oblicz długość ramienia trójkąta.
Ramię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość 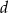 .
.
W trójkącie równoramiennym ramię jest 2 razy dłuższe od podstawy. Suma długości promieni okręgu wpisanego i opisanego na tym trójkącie równa się 11. Oblicz długość podstawy trójkąta.
Dany jest trójkąt równoramienny 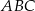 , w którym podstawa
, w którym podstawa 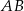 ma długość 32, a każde z ramion
ma długość 32, a każde z ramion 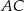 i
i 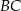 ma długość równą 34. Punkt
ma długość równą 34. Punkt 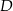 jest środkiem ramienia
jest środkiem ramienia  (zobacz rysunek).
(zobacz rysunek).
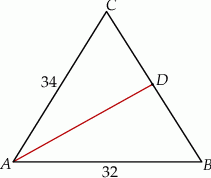
Oblicz długość odcinka 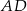 .
.
W trójkącie równoramiennym 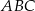 dane są
dane są 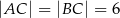 i
i 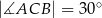 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 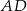 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 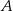 na bok
na bok 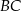 .
.
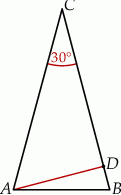
W trójkącie równoramiennym 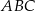 dane są
dane są 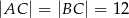 i
i 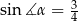 (zobacz rysunek). Oblicz wysokość
(zobacz rysunek). Oblicz wysokość 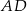 trójkąta opuszczoną z wierzchołka
trójkąta opuszczoną z wierzchołka 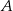 na bok
na bok 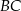 .
.
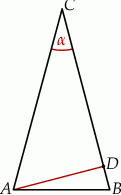
W trójkącie 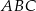 dane są:
dane są: 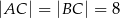 oraz
oraz 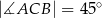 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 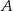 .
.
W trójkącie 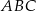 dane są:
dane są: 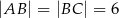 oraz
oraz 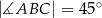 . Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka
. Oblicz długość wysokości tego trójkąta poprowadzonej z wierzchołka 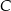 .
.

