Wykaż, że jeżeli liczby 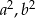 i
i 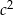 tworzą ciąg arytmetyczny, który nie jest stały, to liczby
tworzą ciąg arytmetyczny, który nie jest stały, to liczby 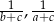 i
i 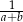 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
/Szkoła średnia/Ciągi/Arytmetyczny/Na dowodzenie
Liczby 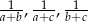 , gdzie
, gdzie 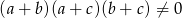 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że liczby 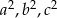 są również wyrazami ciągu arytmetycznego.
są również wyrazami ciągu arytmetycznego.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 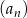 dla każdego
dla każdego 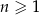 określona jest wzorem
określona jest wzorem 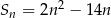 .
.
- Wykaż, że ciąg
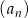 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Wykaż, że jeżeli suma
 początkowych wyrazów ciągu dla każdego
początkowych wyrazów ciągu dla każdego 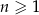 określona jest wzorem
określona jest wzorem 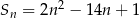 , to ciąg ten nie jest arytmetyczny.
, to ciąg ten nie jest arytmetyczny. - Znajdź takie trzy kolejne wyrazy ciągu
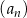 , aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
, aby kwadrat środkowego wyrazu był o 48 mniejszy od różnicy kwadratów wyrazów z nim sąsiadujących.
Sześcian największej z czterech różnych liczb całkowitych, tworzących rosnący ciąg arytmetyczny o wyrazach dodatnich, jest równy sumie sześcianów pozostałych liczb. Wykaż, że iloczyn dwóch z tych liczb jest o 60% większy od iloczynu dwóch pozostałych.
Ciąg 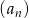 jest określony wzorem
jest określony wzorem 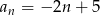 . Uzasadnij (na podstawie definicji) że ciąg
. Uzasadnij (na podstawie definicji) że ciąg 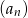 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że ciąg o wzorze ogólnym 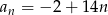 , gdzie
, gdzie 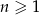 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Dany jest ciąg 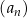 określony wzorem ogólnym
określony wzorem ogólnym 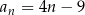 dla każdej liczby naturalnej
dla każdej liczby naturalnej 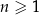 . Wykaż, że ciąg
. Wykaż, że ciąg 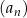 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 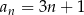 , gdzie
, gdzie 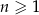 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Wykaż, że ciąg o wzorze ogólnym 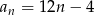 , gdzie
, gdzie 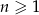 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 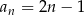 , gdzie
, gdzie 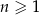 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
W siedmiowyrazowym ciągu arytmetycznym środkowy wyraz jest równy 0. Udowodnij, że suma wyrazów tego ciągu jest równa 0.
Dana jest funkcja określona wzorem 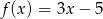 .
.
- Wyznacz ogólny wyraz ciągu
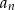 wiedząc, że:
wiedząc, że: 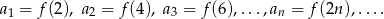
- Uzasadnij, że ciąg
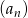 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Oblicz sumę
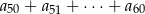 .
.
Wykaż, że liczby 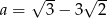 ,
, 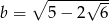 i
i 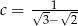 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
Uzasadnij, że jeśli miary kątów wewnętrznych pewnego trójkąta są kolejnymi wyrazami ciągu arytmetycznego, to jeden z tych kątów ma miarę 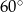 .
.
Dwie dowolne liczby rzeczywiste i ich suma tworzą ciąg arytmetyczny (niekoniecznie w takiej kolejności). Wykaż, że jedna z tych liczb jest dwukrotnością drugiej liczby lub, że liczby te są liczbami przeciwnymi.
Ciągi 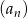 i
i 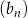 , gdzie
, gdzie 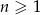 są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg
są ciągami arytmetycznymi. Wykaż, że jeżeli ciąg 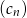 zdefiniowany wzorem
zdefiniowany wzorem 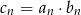 (
(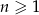 ) jest ciągiem arytmetycznym, to różnica jednego z ciągów
) jest ciągiem arytmetycznym, to różnica jednego z ciągów 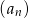 lub
lub 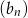 jest równa zeru.
jest równa zeru.
Wykaż, że dla dowolnego ciągu arytmetycznego zachodzi równość 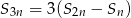 , gdzie
, gdzie 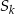 oznacza sumę
oznacza sumę 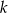 początkowych wyrazów ciągu.
początkowych wyrazów ciągu.
Udowodnij, że jeżeli liczby 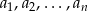 , gdzie
, gdzie 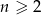 , tworzą ciąg arytmetyczny i żadna z nich nie jest zerem, to
, tworzą ciąg arytmetyczny i żadna z nich nie jest zerem, to
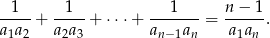
Ciąg 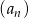 dla
dla 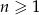 jest ciągiem arytmetycznym oraz
jest ciągiem arytmetycznym oraz 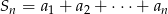 dla
dla 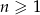 . Wykaż, że jeżeli spełniony jest warunek
. Wykaż, że jeżeli spełniony jest warunek 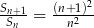 dla
dla 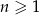 , to spełniony jest również warunek
, to spełniony jest również warunek 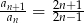 .
.
Ciągi 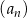 i
i 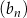 , gdzie
, gdzie 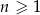 , są ciągami arytmetycznymi. Ciąg
, są ciągami arytmetycznymi. Ciąg 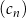 jest określony wzorem
jest określony wzorem 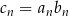 , dla
, dla 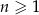 , a ciąg
, a ciąg 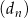 ciągiem różnic dwóch kolejnych wyrazów ciągu
ciągiem różnic dwóch kolejnych wyrazów ciągu 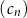 :
: 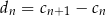 , dla
, dla 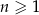 . Wykaż, że ciąg
. Wykaż, że ciąg 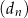 jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów
jest ciągiem arytmetycznym, którego różnica jest równa podwojonemu iloczynowi różnic ciągów 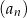 i
i 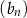 .
.
Wykaż, że jeżeli żadne dwie spośród liczb 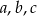 nie są równe oraz liczby
nie są równe oraz liczby 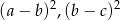 i
i 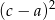 tworzą ciąg arytmetyczny, to liczby
tworzą ciąg arytmetyczny, to liczby 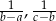 i
i 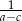 również tworzą ciąg arytmetyczny.
również tworzą ciąg arytmetyczny.
Dany jest ciąg 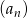 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 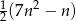 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 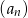 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Wykaż, że dla każdego 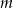 ciąg
ciąg 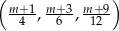 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że dla każdego 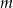 ciąg
ciąg 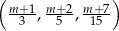 jest arytmetyczny.
jest arytmetyczny.

