Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 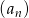 wyraża się wzorem
wyraża się wzorem 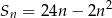 , gdzie
, gdzie 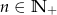 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 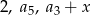 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Różne
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 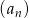 wyraża się wzorem
wyraża się wzorem 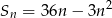 , gdzie
, gdzie 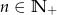 . Oblicz
. Oblicz  wiedząc, że liczby:
wiedząc, że liczby: 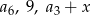 w podanej kolejności tworzą ciąg geometryczny.
w podanej kolejności tworzą ciąg geometryczny.
Ciąg 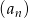 dany jest wzorem
dany jest wzorem 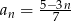 , dla
, dla 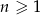 .
.
- Oblicz sumę
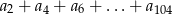 .
. - Ustalmy
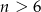 . Dla jakich
. Dla jakich  liczby
liczby 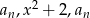 są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Dane są dwa ciągi rosnące: arytmetyczny 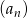 i geometryczny
i geometryczny 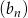 . Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
. Pierwsze wyrazy obu ciągów są równe 2, trzecie ich wyrazy są takie same, a jedenasty wyraz ciągu arytmetycznego jest równy piątemu wyrazowi ciągu geometrycznego. Wyznacz te ciągi zapisując wzory na wyrazy ogólne.
Ciąg 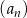 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 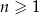 , jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto
, jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto 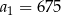 i
i 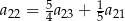 . Ciąg
. Ciąg 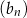 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 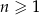 , jest arytmetyczny. Suma wszystkich wyrazów ciągu
, jest arytmetyczny. Suma wszystkich wyrazów ciągu 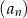 jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu
jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu 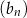 . Ponadto
. Ponadto 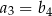 . Oblicz
. Oblicz 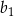 .
.
Szósty wyraz ciągu arytmetycznego 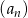 jest o 6 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na
jest o 6 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na  –ty wyraz ciągu
–ty wyraz ciągu 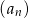 , wiedząc, że ciąg
, wiedząc, że ciąg 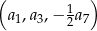 jest geometryczny.
jest geometryczny.
Szósty wyraz ciągu arytmetycznego 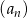 jest o 4 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na
jest o 4 mniejszy od czwartego wyrazu. Wyznacz wzór ogólny na  –ty wyraz ciągu
–ty wyraz ciągu 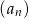 , wiedząc, że ciąg
, wiedząc, że ciąg 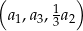 jest geometryczny.
jest geometryczny.
Ciąg 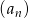 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 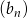 jest geometryczny. Pierwszy wyraz
jest geometryczny. Pierwszy wyraz 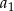 ciągu arytmetycznego jest ilorazem ciągu geometrycznego
ciągu arytmetycznego jest ilorazem ciągu geometrycznego 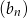 . Wyrazy ciągu
. Wyrazy ciągu 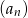 są liczbami całkowitymi, a suma ośmiu początkowych wyrazów tego ciągu jest równa 124. Natomiast pierwszy wyraz
są liczbami całkowitymi, a suma ośmiu początkowych wyrazów tego ciągu jest równa 124. Natomiast pierwszy wyraz 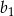 ciągu geometrycznego jest różnicą ciągu arytmetycznego
ciągu geometrycznego jest różnicą ciągu arytmetycznego 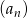 . Suma dwóch pierwszych wyrazów ciągu geometrycznego
. Suma dwóch pierwszych wyrazów ciągu geometrycznego 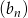 jest równa 18. Wyznacz te ciągi.
jest równa 18. Wyznacz te ciągi.
Ciąg 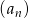 jest geometryczny, a ciąg
jest geometryczny, a ciąg 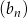 jest arytmetyczny. Pierwszy wyraz
jest arytmetyczny. Pierwszy wyraz 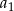 ciągu geometrycznego jest różnicą ciągu arytmetycznego
ciągu geometrycznego jest różnicą ciągu arytmetycznego 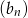 . Wyrazy ciągu
. Wyrazy ciągu 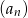 są liczbami całkowitymi, a suma dwóch początkowych wyrazów tego ciągu jest równa 28. Natomiast pierwszy wyraz
są liczbami całkowitymi, a suma dwóch początkowych wyrazów tego ciągu jest równa 28. Natomiast pierwszy wyraz 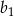 ciągu arytmetycznego jest ilorazem ciągu geometrycznego
ciągu arytmetycznego jest ilorazem ciągu geometrycznego 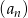 . Suma siedmiu pierwszych wyrazów ciągu arytmetycznego
. Suma siedmiu pierwszych wyrazów ciągu arytmetycznego 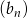 jest równa 126. Wyznacz te ciągi.
jest równa 126. Wyznacz te ciągi.
Liczba  jest pierwszym wyrazem ciągu geometrycznego
jest pierwszym wyrazem ciągu geometrycznego 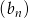 , którego iloraz jest równy
, którego iloraz jest równy 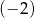 . Pierwszy wyraz ciągu arytmetycznego
. Pierwszy wyraz ciągu arytmetycznego 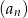 jest taki sam jak pierwszy wyraz ciągu
jest taki sam jak pierwszy wyraz ciągu 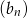 . Suma siedmiu początkowych wyrazów ciągu
. Suma siedmiu początkowych wyrazów ciągu 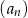 jest równa sumie siedmiu początkowych wyrazów ciągu
jest równa sumie siedmiu początkowych wyrazów ciągu 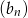 . Oblicz różnicę ciągu arytmetycznego
. Oblicz różnicę ciągu arytmetycznego 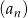 .
.
Ciąg 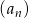 , gdzie
, gdzie 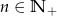 , jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy
, jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy 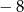 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 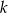 , dla których trzywyrazowy ciąg
, dla których trzywyrazowy ciąg 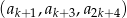 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
Ciąg 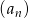 , gdzie
, gdzie 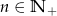 , jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy
, jest nieskończonym ciągiem arytmetycznym o różnicy 2, w którym pierwszy wyraz jest równy 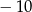 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 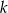 , dla których trzywyrazowy ciąg
, dla których trzywyrazowy ciąg 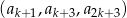 jest ciągiem geometrycznym.
jest ciągiem geometrycznym.
W nieskończonym rosnącym ciągu geometrycznym 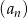 o wyrazach dodatnich, określonym dla
o wyrazach dodatnich, określonym dla 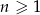 , stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy
, stosunek średniej geometrycznej trzech pierwszych wyrazów do średniej arytmetycznej tych wyrazów jest równy 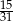 , a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy
, a suma czterech pierwszych wyrazów tego ciągu jest równa 468. Wyrazy 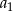 i
i 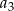 ciągu
ciągu 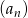 , są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego
, są odpowiednio pierwszym i trzecim wyrazem ciągu arytmetycznego 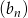 . Oblicz sumę 10 początkowych wyrazów ciągu
. Oblicz sumę 10 początkowych wyrazów ciągu 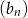 .
.
Uwaga: średnia geometryczna liczb 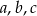 jest równa
jest równa 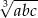 .
.
W ciągu arytmetycznym wyraz pierwszy jest równy 1, a ostatni 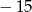 . Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.
. Oblicz sumę wyrazów tego ciągu, jeśli wiadomo że drugi, trzeci i szósty są kolejnymi wyrazami ciągu geometrycznego.
Dany jest ciąg 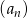 o wyrazie ogólnym
o wyrazie ogólnym 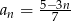 , dla
, dla 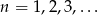 .
.
- Sprawdź, czy ciąg
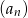 jest arytmetyczny.
jest arytmetyczny. - Oblicz, dla jakiej wartości
 liczby
liczby 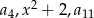 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
W dziewięciowyrazowym ciągu arytmetycznym, o pierwszym wyrazie równym 4, wyraz pierwszy, trzeci i siódmy tworzą ciąg geometryczny. Oblicz sumę wyrazów tego ciągu arytmetycznego
Obroty pewnej firmy w pierwszych trzech kwartałach 2007 roku utworzyły ciąg geometryczny, a w ciągu ostatnich trzech kwartałów ciąg arytmetyczny. W drugim kwartale obroty firmy wynosiły 15 000 zł, a w czwartym 22 500 zł. Oblicz średnie miesięczne obroty firmy.
Ciąg 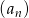 określony jest wzorem
określony jest wzorem 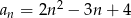 .
.
- Trzeci i piąty wyraz ciągu
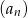 są odpowiednio równe szóstemu i dziewiętnastemu wyrazowi ciągu arytmetycznego
są odpowiednio równe szóstemu i dziewiętnastemu wyrazowi ciągu arytmetycznego 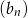 . Ile początkowych wyrazów ciągu arytmetycznego
. Ile początkowych wyrazów ciągu arytmetycznego 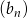 należy dodać, aby otrzymana suma była nie mniejsza od 483?
należy dodać, aby otrzymana suma była nie mniejsza od 483? - Piąty oraz trzeci wyraz ciągu
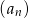 są odpowiednio równe pierwszemu i drugiemu wyrazowi nieskończonego ciągu geometrycznego
są odpowiednio równe pierwszemu i drugiemu wyrazowi nieskończonego ciągu geometrycznego 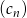 . Który wyraz ciągu
. Który wyraz ciągu 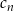 jest równy
jest równy 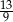 ?
?
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
Rosnący ciąg arytmetyczny 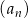 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 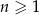 . Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy
. Suma pierwszych dwunastu wyrazów tego ciągu jest równa 240. Wyrazy 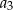 ,
, 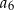 ,
, 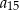 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego  .
.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 40, a wyrazy drugi, piąty i dwudziesty trzeci tworzą w podanej kolejności ciąg geometryczny.
Rosnący ciąg arytmetyczny 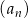 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 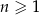 . Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy
. Suma pierwszych pięciu wyrazów tego ciągu jest równa 10. Wyrazy 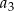 ,
, 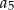 ,
, 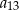 tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na
tworzą – w podanej kolejności – ciąg geometryczny. Wyznacz wzór na  –ty wyraz ciągu arytmetycznego
–ty wyraz ciągu arytmetycznego 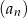 .
.
W nieskończonym ciągu arytmetycznym 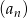 , określonym dla
, określonym dla 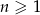 , suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy
, suma jedenastu początkowych wyrazów tego ciągu jest równa 187. Średnia arytmetyczna pierwszego, trzeciego i dziewiątego wyrazu tego ciągu, jest równa 12. Wyrazy 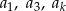 ciągu
ciągu 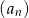 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 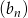 . Oblicz
. Oblicz 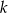 .
.
W nieskończonym ciągu arytmetycznym 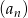 , określonym dla
, określonym dla 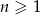 , suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy
, suma dziewięciu początkowych wyrazów jest równa 171. Średnia arytmetyczna pierwszego, trzeciego i ósmego wyrazu tego ciągu, jest równa 15. Wyrazy 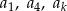 ciągu
ciągu 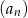 , w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny
, w podanej kolejności, tworzą nowy ciąg – trzywyrazowy ciąg geometryczny 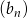 . Oblicz
. Oblicz 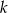 .
.
Pierwszy, trzeci i trzynasty wyraz ciągu arytmetycznego 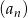 ,
, 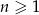 są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu
są kolejnymi wyrazami ciągu geometrycznego. Piąty wyraz ciągu 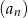 jest równy 27. Wyznacz wzór ciągu
jest równy 27. Wyznacz wzór ciągu 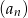 wiedząc, że nie jest to ciąg stały.
wiedząc, że nie jest to ciąg stały.
Dany jest nieskończony rosnący ciąg arytmetyczny 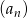 , dla
, dla 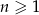 taki, że
taki, że 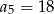 . Wyrazy
. Wyrazy 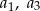 oraz
oraz 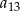 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 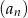 .
.
Dany jest nieskończony rosnący ciąg arytmetyczny 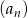 , dla
, dla 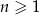 taki, że
taki, że 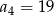 . Wyrazy
. Wyrazy 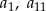 oraz
oraz 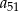 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 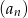 .
.
Pierwszy wyraz ciągu arytmetycznego 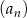 jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
- Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
- Dla jakiego
 liczby
liczby 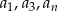 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Pierwszy wyraz ciągu arytmetycznego 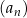 jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
-
Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
-
Dla jakiego
 liczby
liczby 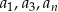 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Dany jest ciąg arytmetyczny 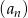 o różnicy
o różnicy 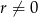 i pierwszym wyrazie
i pierwszym wyrazie 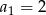 . Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
. Pierwszy, drugi i czwarty wyraz tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Oblicz iloraz tego ciągu geometrycznego.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.

