Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.

Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
Jeden z boków równoległoboku jest o 2,5 cm krótszy od drugiego boku. Obwód tego równoległoboku jest równy 29 cm. Oblicz długości jego boków.
Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
Na rysunku przedstawiono dwa równoległoboki 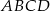 i
i 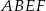 . Uzasadnij, że czworokąty
. Uzasadnij, że czworokąty 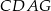 oraz
oraz 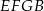 mają równe pola.
mają równe pola.
Boki równoległoboku mają długości 4 cm i 6 cm, a wysokość opuszczona na dłuższy bok ma długość 3 cm. Oblicz długość drugiej wysokości tego równoległoboku.
Boki równoległoboku mają długości 6 cm i 8 cm, a wysokość opuszczona na dłuższy bok ma długość 3 cm. Oblicz długość drugiej wysokości tego równoległoboku.
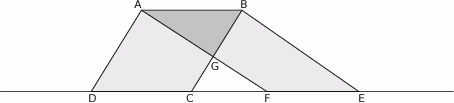
W równoległoboku 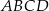 punkt
punkt 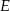 jest takim punktem boku
jest takim punktem boku 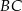 , że
, że 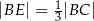 . Z wierzchołka
. Z wierzchołka 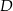 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 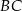 w punkcie
w punkcie 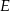 . Proste
. Proste 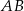 i
i 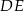 przecinają się w punkcie
przecinają się w punkcie 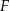 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 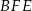 stanowi
stanowi 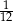 pola równoległoboku
pola równoległoboku 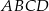 .
.
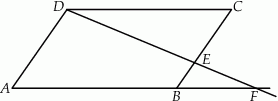
Punkt 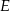 jest środkiem boku
jest środkiem boku 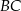 równoległoboku
równoległoboku 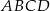 , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 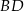 w punkcie
w punkcie 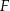 . Wykaż, że
. Wykaż, że 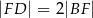 .
.
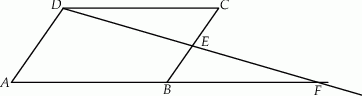
W równoległoboku 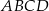 punkt
punkt 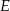 jest środkiem boku
jest środkiem boku 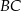 . Z wierzchołka
. Z wierzchołka 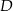 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 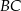 w punkcie
w punkcie 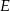 . Proste
. Proste 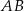 i
i 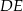 przecinają się w punkcie
przecinają się w punkcie 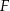 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt 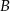 jest środkiem odcinka
jest środkiem odcinka 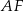 .
.
Punkt 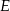 jest środkiem boku
jest środkiem boku 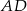 równoległoboku
równoległoboku 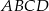 . Pole trójkąta
. Pole trójkąta 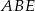 jest równe 2. Oblicz pole równoległoboku.
jest równe 2. Oblicz pole równoległoboku.
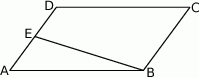
Równoległobok 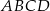 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości 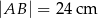 i
i 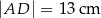 .
.
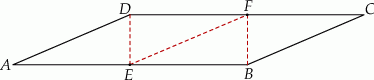
Oblicz pole równoległoboku 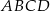 .
.
Równoległobok 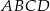 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości 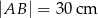 i
i 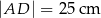 .
.
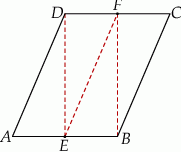
Oblicz pole równoległoboku 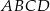 .
.
Równoległobok 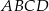 o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej
o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej  na dwa trapezy tak, jak pokazano na rysunku. Odcinek
na dwa trapezy tak, jak pokazano na rysunku. Odcinek 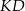 ma długość 4,8 cm.
ma długość 4,8 cm.
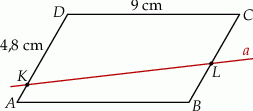
Pole trapezu 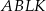 jest trzykrotnie mniejsze od pola równoległoboku
jest trzykrotnie mniejsze od pola równoległoboku 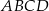 . Oblicz długość odcinka
. Oblicz długość odcinka 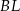 . Zapisz obliczenia.
. Zapisz obliczenia.
Ada wycięła z kartonu równoległobok 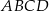 o bokach
o bokach 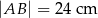 ,
, 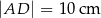 i polu równym
i polu równym 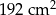 (rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej
(rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej 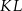 i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
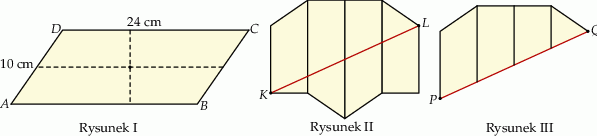
Oblicz obwód wielokąta z rysunku III.
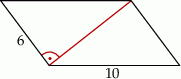
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
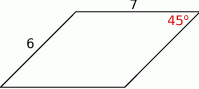
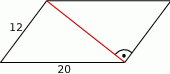
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
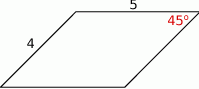
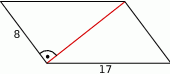
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
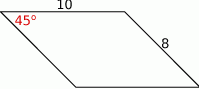
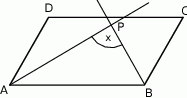
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
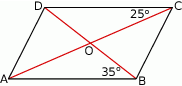
Oblicz miarę kąta rozwartego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
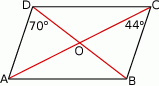
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
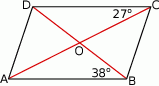
Na rysunku przedstawiono równoległobok  i trójkąt
i trójkąt  . Punkt
. Punkt 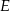 leży na odcinku
leży na odcinku 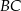 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 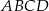 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 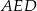 .
.
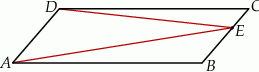
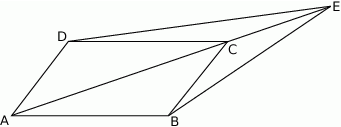
Dany jest równoległobok 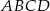 . Na przedłużeniu przekątnej
. Na przedłużeniu przekątnej 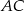 wybrano punkt
wybrano punkt 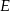 tak, że
tak, że 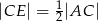 (zobacz rysunek). Uzasadnij, że pole równoległoboku
(zobacz rysunek). Uzasadnij, że pole równoległoboku 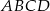 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 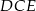 .
.
Na przekątnej 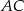 równoległoboku
równoległoboku 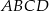 wybrano punkt
wybrano punkt 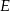 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 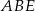 i
i  mają równe pola.
mają równe pola.
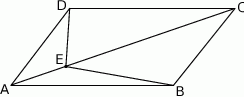
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest większa od miary drugiego o 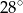 .
.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest większa od miary drugiego o 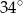 .
.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest 5 razy większa od miary drugiego.
Wyznacz kąty równoległoboku, jeśli miara jednego z nich jest 4 razy większa od miary drugiego.
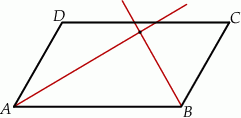
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Uzasadnij, że dwusieczne kątów 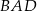 i
i 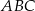 równoległoboku
równoległoboku 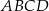 są prostopadłe.
są prostopadłe.
W równoległoboku 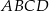 przekątna
przekątna 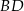 ma długość
ma długość 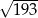 , a wysokość
, a wysokość 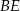 dzieli bok
dzieli bok 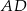 na odcinki o długościach
na odcinki o długościach 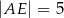 i
i 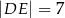 (zobacz rysunek).
(zobacz rysunek).
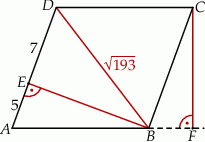
Oblicz długość wysokości 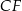 tego równoległoboku.
tego równoległoboku.
Półprosta 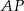 jest dwusieczną kąta
jest dwusieczną kąta 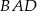 i półprosta
i półprosta 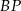 jest dwusieczną kąta
jest dwusieczną kąta 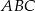 w równoległoboku
w równoległoboku 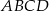 . Kąt
. Kąt 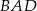 jest równy
jest równy 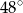 . Oblicz miarę kąta
. Oblicz miarę kąta 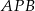 . Zapisz obliczenia.
. Zapisz obliczenia.