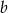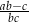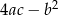Wyznacz wszystkie funkcje kwadratowe, których wykres przechodzi przez punkty 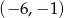 oraz
oraz 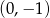 .
.
/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/3 niewiadome
Punkty 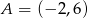 i
i 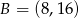 należą do wykresu funkcji
należą do wykresu funkcji 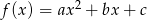 . Funkcja
. Funkcja 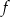 ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej
ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej 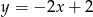 . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
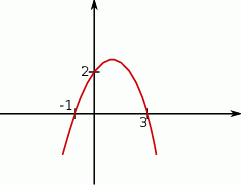
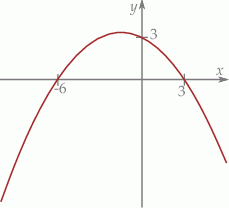
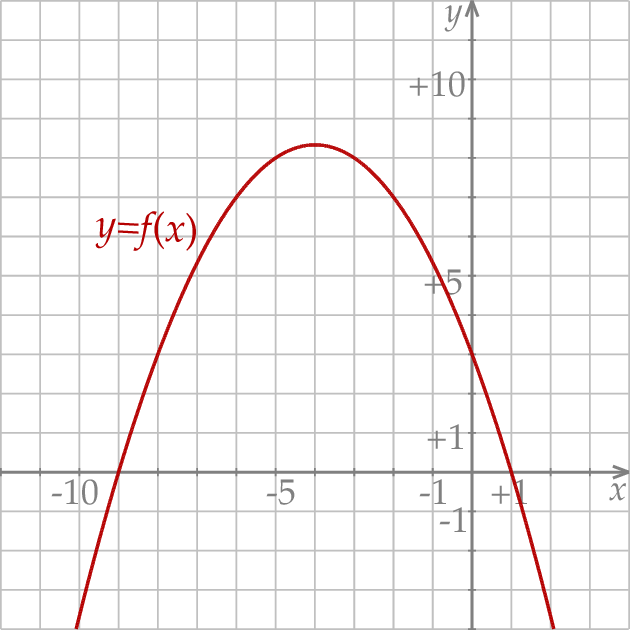
Na podstawie wykresu funkcji kwadratowej podaj jej wzór.
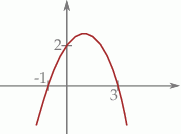
Na podstawie przedstawionego fragmentu wykresu funkcji kwadratowej wyznacz jej wzór.
Wykres funkcji kwadratowej 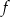 jest styczny do prostej
jest styczny do prostej 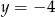 , przechodzi przez punkt
, przechodzi przez punkt 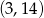 oraz jest symetryczny względem osi
oraz jest symetryczny względem osi 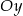 .
.
- Wyznacz wzór funkcji
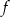 i narysuj jej wykres.
i narysuj jej wykres. - Rozwiąż nierówność
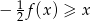
Dany jest wykres funkcji kwadratowej 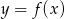
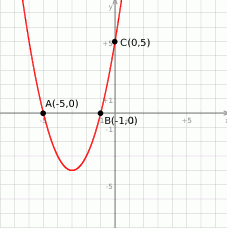
- Korzystając z danych na wykresie wyznacz wzór funkcji
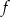 w postaci ogólnej.
w postaci ogólnej. - Oblicz współrzędne wierzchołka paraboli.
- Podaj zbiór rozwiązań nierówności
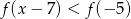 .
.
Napisz w postaci ogólnej, kanonicznej i iloczynowej wzór funkcji kwadratowej, jeśli do wykresu tej funkcji należy punkt 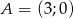 i funkcja osiąga wartość największą równą 12 dla argumentu 1.
i funkcja osiąga wartość największą równą 12 dla argumentu 1.
Funkcja kwadratowa 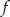 dla
dla 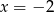 przyjmuje wartość największą równą 1. Do wykresu funkcji
przyjmuje wartość największą równą 1. Do wykresu funkcji 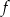 należy punkt
należy punkt 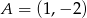 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 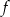 .
.
Funkcja kwadratowa, 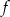 dla
dla 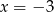 przyjmuje wartość największą równą 4. Do wykresu funkcji
przyjmuje wartość największą równą 4. Do wykresu funkcji 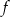 należy punkt
należy punkt 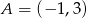 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 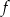 .
.
Dana jest funkcja kwadratowa 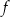 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji 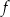 jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
Wyznacz zbiór wartości funkcji  .
.
W kartezjańskim układzie współrzędnych  przedstawiono oś symetrii wykresu funkcji kwadratowej
przedstawiono oś symetrii wykresu funkcji kwadratowej  . Przedstawiono również prostą
. Przedstawiono również prostą 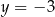 , z którą wykres funkcji
, z którą wykres funkcji 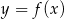 ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu –
ma dokładnie jeden punkt wspólny, oraz jeden z punktów tego wykresu – 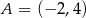
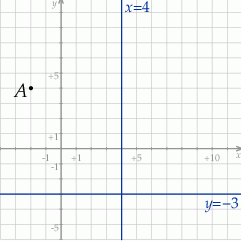
Wyznacz wzór funkcji kwadratowej 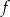 w postaci kanonicznej.
w postaci kanonicznej.
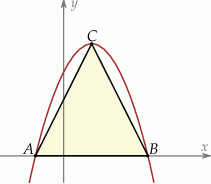
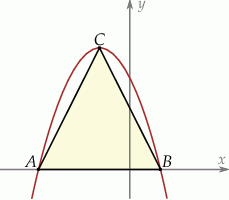
Wierzchołki trójkąta 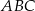 leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej
leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej 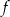 (zobacz rysunek). Pole tego trójkąta jest równe 8, punkt
(zobacz rysunek). Pole tego trójkąta jest równe 8, punkt 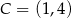 jest wierzchołkiem paraboli, a punkty
jest wierzchołkiem paraboli, a punkty 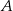 i
i 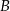 leżą na osi
leżą na osi 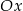 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 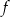 .
.
Wierzchołki trójkąta  leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej
leżą na paraboli, która jest wykresem pewnej funkcji kwadratowej  (zobacz rysunek). Pole tego trójkąta jest równe 8, punkt
(zobacz rysunek). Pole tego trójkąta jest równe 8, punkt 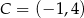 jest wierzchołkiem paraboli, a punkty
jest wierzchołkiem paraboli, a punkty 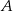 i
i 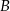 leżą na osi
leżą na osi 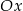 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 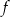 .
.
Znajdź wzór funkcji kwadratowej 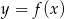 , której wykresem jest parabola o wierzchołku
, której wykresem jest parabola o wierzchołku 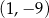 przechodząca przez punkt o współrzędnych
przechodząca przez punkt o współrzędnych 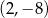 . Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
. Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
Wykresem funkcji kwadratowej 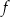 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 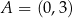 . Punkt
. Punkt 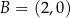 leży na wykresie funkcji
leży na wykresie funkcji 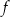 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 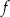 .
.
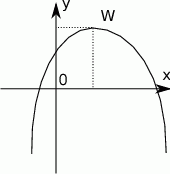
Wykorzystując poniższy szkic wykresu funkcji kwadratowej o równaniu 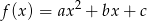 , gdzie
, gdzie 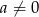 określ znak następujących wyrażeń:
określ znak następujących wyrażeń:
Dana jest funkcja kwadratowa 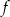 , której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych
, której fragment wykresu przedstawiono w kartezjańskim układzie współrzędnych 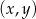 na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 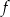 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
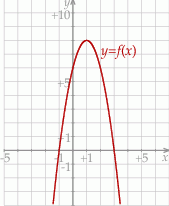
Wyznacz wzór funkcji kwadratowej 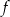 w postaci kanonicznej.
w postaci kanonicznej.
W kartezjańskim układzie współrzędnych 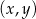 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 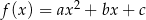 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 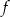 , ma współrzędne
, ma współrzędne 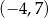 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 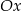 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 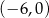 .
.
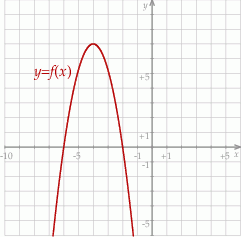
Wyznacz wzór funkcji kwadratowej 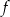 w postaci kanonicznej.
w postaci kanonicznej.
W kartezjańskim układzie współrzędnych 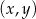 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 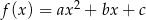 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 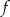 , ma współrzędne
, ma współrzędne 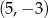 . Jeden z punktów przecięcia paraboli z osią
. Jeden z punktów przecięcia paraboli z osią 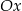 układu współrzędnych ma współrzędne
układu współrzędnych ma współrzędne 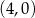 .
.
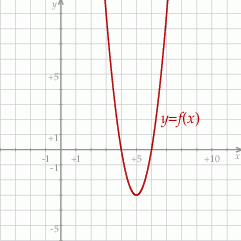
Wyznacz wzór funkcji kwadratowej 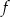 w postaci kanonicznej.
w postaci kanonicznej.
Dana jest funkcja kwadratowa 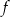 , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 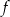 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
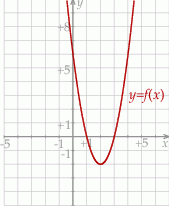
Wyznacz wzór funkcji kwadratowej 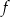 w postaci kanonicznej.
w postaci kanonicznej.
Napisz wzór funkcji kwadratowej w postaci ogólnej wiedząc, że funkcja ma jedno miejsce zerowe oraz do jej wykresu należą punkty 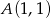 oraz
oraz 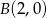 .
.
Parabola, która jest wykresem funkcji kwadratowej 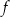 , ma z osiami kartezjańskiego układu współrzędnych
, ma z osiami kartezjańskiego układu współrzędnych 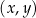 dokładnie dwa punkty wspólne:
dokładnie dwa punkty wspólne: 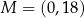 oraz
oraz 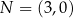 . Wyznacz wzór funkcji kwadratowej
. Wyznacz wzór funkcji kwadratowej 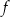 .
.
Pewna parabola o wierzchołku 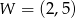 przecina oś
przecina oś 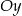 w punkcie
w punkcie 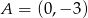 .
.
- Wyznacz postać ogólną funkcji kwadratowej
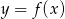 , której wykresem jest ta parabola.
, której wykresem jest ta parabola. - Rozwiąż nierówność
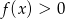 .
.
Wykres funkcji kwadratowej 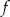 określonej wzorem
określonej wzorem 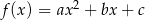 ma z prostą o równaniu
ma z prostą o równaniu 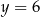 dokładnie jeden punkt wspólny. Punkty
dokładnie jeden punkt wspólny. Punkty 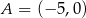 i
i 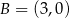 należą do wykresu funkcji
należą do wykresu funkcji 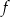 . Oblicz wartości współczynników
. Oblicz wartości współczynników 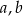 oraz
oraz  .
.
Wykresem funkcji 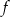 jest parabola, której wierzchołkiem jest punkt
jest parabola, której wierzchołkiem jest punkt 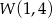 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 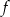 w przedziale
w przedziale 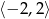 wynosi -5.
wynosi -5.
- Przedstaw wzór funkcji
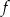 w postaci iloczynowej.
w postaci iloczynowej. - Rozwiąż nierówność
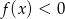 .
.
Na podstawie wykresu funkcji kwadratowej podaj jej wzór w postaci ogólnej, kanonicznej oraz iloczynowej.