Uczeń przeczytał w ciągu tygodnia książkę liczącą 420 stron.
| Dzień | Liczba przeczytanych stron | Czas czytania |
| 1. | 50 | 1 h 40 min |
| 2. | 70 | 2 h |
| 3. | 90 | 2 h 20 min |
| 4. | 30 | 30 min |
| 5. | 70 | 2 h 10 min |
| 6. | 80 | 2 h 30 min |
| 7. | 30 | 30 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie prawdziwe.
A) Pierwszego dnia uczeń przeczytał ponad 20% całej książki.
B) Uczeń czytał średnio 50 stron dziennie.
C) Piątego dnia uczeń przeczytał 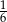 całej książki.
całej książki.
D) Przeczytanie pierwszej połowy książki zajęło uczniowi mniej czasu niż przeczytanie drugiej połowy.

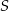 potrzeba tyle samo materiału, ile na uszycie 60 jednakowych bluzek w rozmiarze
potrzeba tyle samo materiału, ile na uszycie 60 jednakowych bluzek w rozmiarze 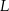 . Przyjmij, że na uszycie większej lub mniejszej liczby bluzek potrzeba proporcjonalnie więcej lub mniej materiału.
. Przyjmij, że na uszycie większej lub mniejszej liczby bluzek potrzeba proporcjonalnie więcej lub mniej materiału.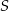 potrzeba tyle samo materiału, ile potrzeba na uszycie A/B bluzek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie A/B bluzek w rozmiarze 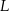 .
.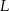 potrzeba tyle samo materiału, ile potrzeba na uszycie C/D bluzek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie C/D bluzek w rozmiarze 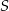 .
.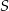 potrzeba tyle samo materiału, ile na uszycie 90 jednakowych czapek w rozmiarze
potrzeba tyle samo materiału, ile na uszycie 90 jednakowych czapek w rozmiarze 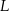 . Przyjmij, że na uszycie większej lub mniejszej liczby czapek potrzeba proporcjonalnie więcej lub mniej materiału.
. Przyjmij, że na uszycie większej lub mniejszej liczby czapek potrzeba proporcjonalnie więcej lub mniej materiału.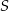 potrzeba tyle samo materiału, ile potrzeba na uszycie A/B czapek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie A/B czapek w rozmiarze 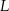 .
.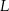 potrzeba tyle samo materiału, ile potrzeba na uszycie C/D czapek w rozmiarze
potrzeba tyle samo materiału, ile potrzeba na uszycie C/D czapek w rozmiarze 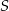 .
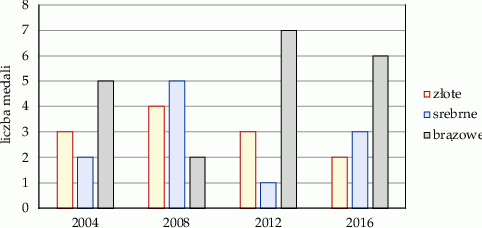
.

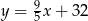 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 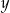 - temperatura w skali Fahrenheita. Zatem 122 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 122 stopnie Fahrenheita są równe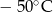
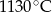
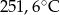
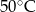
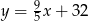 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 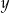 - temperatura w skali Fahrenheita. Zatem 59 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 59 stopnie Fahrenheita są równe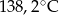
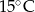
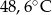
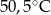
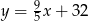 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 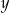 - temperatura w skali Fahrenheita. Zatem 113 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 113 stopnie Fahrenheita są równe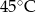
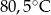
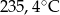
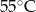


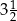 szklanki mąki.
szklanki mąki. 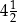 szklanki mleka.
szklanki mleka. 
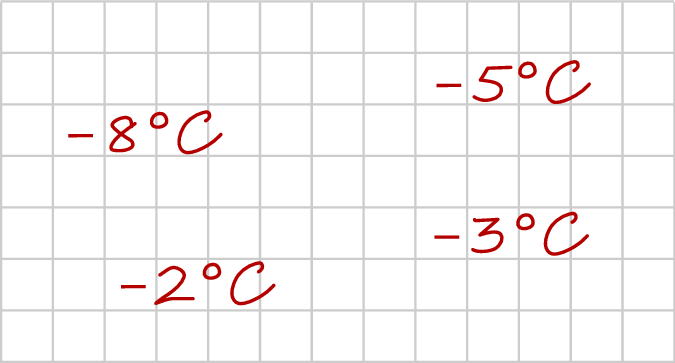
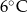 wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę
wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę 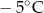 zanotowano w
zanotowano w 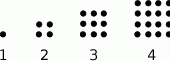
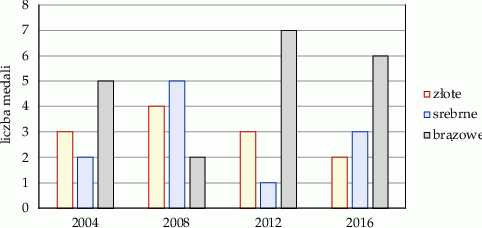
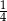 swoich.
swoich.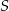 wyrzuconych oczek według następującej reguły: jeżeli liczba wyrzuconych oczek była nieparzysta, to dodawała tę liczbę do sumy
wyrzuconych oczek według następującej reguły: jeżeli liczba wyrzuconych oczek była nieparzysta, to dodawała tę liczbę do sumy 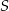 , a jeżeli liczba wyrzuconych oczek była parzysta, to odejmowała tę liczbę od
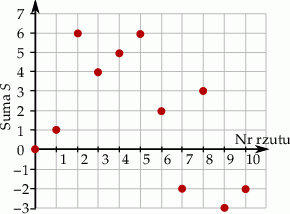
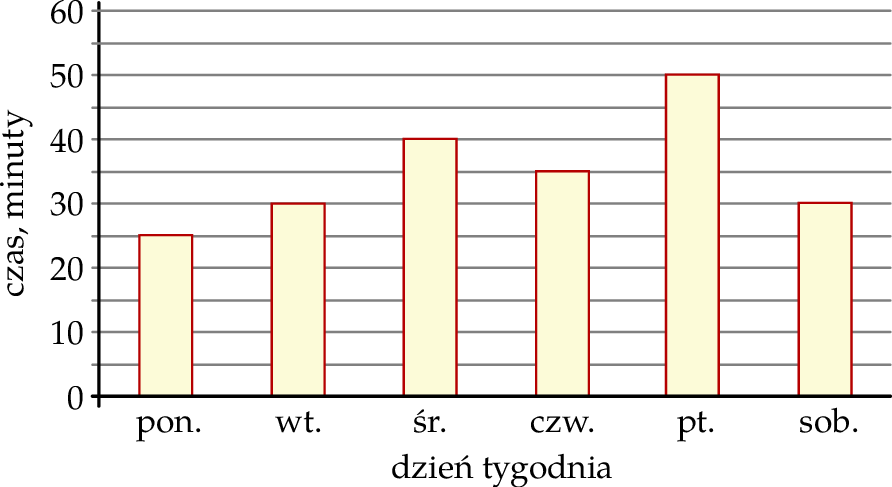
, a jeżeli liczba wyrzuconych oczek była parzysta, to odejmowała tę liczbę od 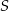 . Na diagramie przedstawiono wartości sumy
. Na diagramie przedstawiono wartości sumy 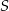 po kolejnych rzutach.
po kolejnych rzutach.