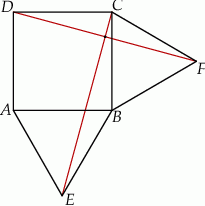
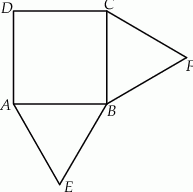
Na zewnątrz kwadratu 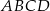 na bokach
na bokach 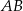 i
i 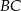 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 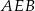 i
i 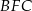 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 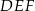 jest równoboczny.
jest równoboczny.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na zewnątrz kwadratu 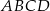 na bokach
na bokach 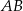 i
i 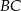 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 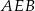 i
i 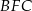 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 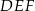 jest równoboczny.
jest równoboczny.

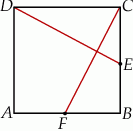
Na rysunku przedstawiono kwadrat 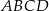 . Punkty
. Punkty 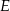 i
i 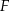 są środkami boków
są środkami boków 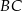 i
i 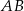 . Uzasadnij, że odcinki
. Uzasadnij, że odcinki 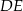 i
i 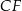 są prostopadłe.
są prostopadłe.
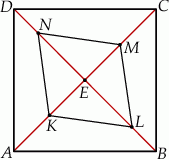
Dany jest kwadrat 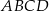 . Przekątne
. Przekątne 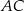 i
i 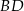 przecinają się w punkcie
przecinają się w punkcie 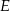 . Punkty
. Punkty 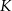 i
i 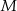 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 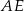 i
i 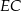 . Punkty
. Punkty 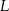 i
i 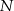 leżą na przekątnej
leżą na przekątnej 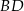 tak, że
tak, że 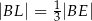 i
i 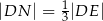 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 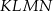 do pola kwadratu
do pola kwadratu  jest równy 1:3.
jest równy 1:3.
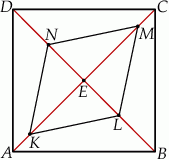
Dany jest kwadrat  . Przekątne
. Przekątne  i
i 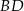 przecinają się w punkcie
przecinają się w punkcie 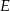 . Punkty
. Punkty 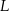 i
i 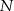 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 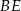 i
i 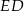 . Punkty
. Punkty 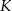 i
i 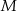 leżą na przekątnej
leżą na przekątnej 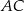 tak, że
tak, że 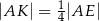 i
i 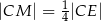 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 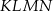 do pola kwadratu
do pola kwadratu 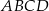 jest równy 3:8.
jest równy 3:8.
Koło i kwadrat mają równe obwody. Wykaż, że pierwsza z tych figur ma większe pole.
Prosta przechodząca przez wierzchołek 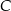 kwadratu
kwadratu 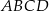 przecina przedłużenia jego boków
przecina przedłużenia jego boków 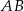 i
i 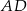 odpowiednio w punktach
odpowiednio w punktach 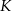 i
i 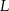 (zobacz rysunek).
(zobacz rysunek).
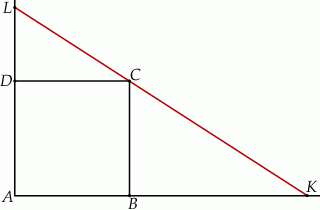
Wykaż, że
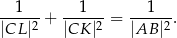
Punkt 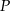 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 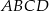 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 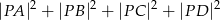 ma stałą wartość, niezależną od wyboru punktu
ma stałą wartość, niezależną od wyboru punktu 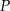 .
.
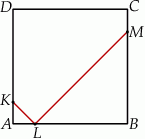
Na bokach 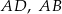 i
i 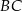 kwadratu
kwadratu 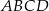 wybrano punkty
wybrano punkty 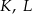 i
i 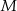 w ten sposób, że
w ten sposób, że 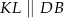 i
i 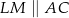 . Uzasadnij, że
. Uzasadnij, że 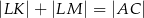 .
.
Prosta przechodząca przez środek 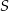 kwadratu
kwadratu 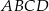 przecina proste zawierające jego boki
przecina proste zawierające jego boki 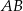 i
i 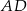 odpowiednio w punktach
odpowiednio w punktach 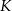 i
i 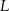 (zobacz rysunek).
(zobacz rysunek).
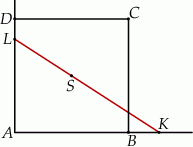
Wykaż, że
Wykaż, że stosunek długości promienia okręgu opisanego na kwadracie do długości promienia wpisanego w ten kwadrat jest równy 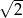 .
.
Wykaż, że stosunek długości promienia okręgu wpisanego w kwadrat do długości promienia okręgu opisanego na kwadracie jest równy 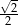 .
.
Bok 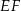 kwadratu
kwadratu 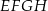 zawiera się w przekątnej
zawiera się w przekątnej 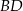 kwadratu
kwadratu 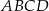 , a punkt
, a punkt 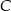 należy do odcinka
należy do odcinka 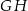 . Odcinki
. Odcinki 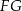 i
i 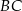 przecinają się w punkcie
przecinają się w punkcie 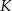 , a odcinki
, a odcinki 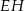 i
i 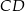 przecinają się w punkcie
przecinają się w punkcie 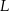 . Wykaż, że
. Wykaż, że 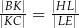 .
.
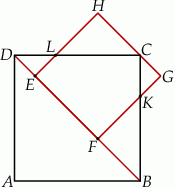
Bok 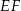 kwadratu
kwadratu 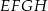 zawiera się w przekątnej
zawiera się w przekątnej 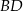 kwadratu
kwadratu 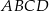 , a punkt
, a punkt 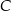 jest środkiem odcinka
jest środkiem odcinka 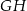 . Odcinki
. Odcinki 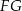 i
i 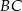 przecinają się w punkcie
przecinają się w punkcie 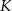 . Wykaż, że
. Wykaż, że 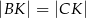 .
.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 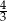 .
.
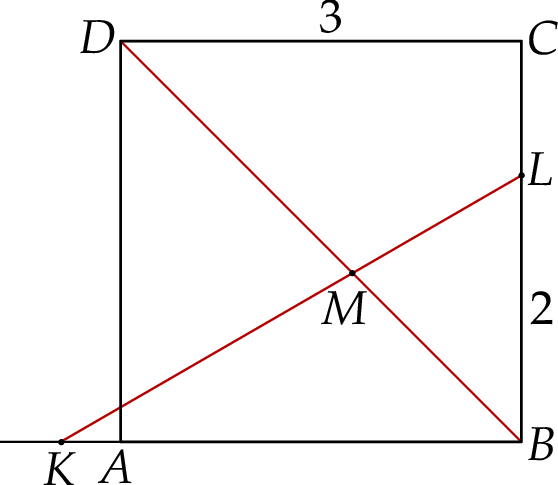
Dany jest kwadrat 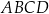 o boku długości 3. Punkty
o boku długości 3. Punkty 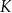 i
i 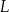 leżą na prostych – odpowiednio –
leżą na prostych – odpowiednio – 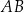 i
i 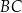 tak, że
tak, że 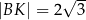 i
i 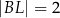 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 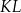 przecina przekątną
przecina przekątną 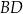 tego kwadratu w punkcie
tego kwadratu w punkcie 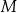 .
.
Wykaż, że 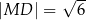 .
.
Pole kwadratu 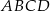 jest równe 16. Punkt
jest równe 16. Punkt 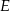 jest środkiem boku
jest środkiem boku 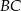 , a punkt
, a punkt 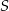 punktem przecięcia przekątnej
punktem przecięcia przekątnej 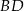 kwadratu i odcinka
kwadratu i odcinka 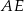 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 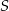 od boku
od boku 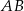 jest równa
jest równa 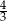 .
.
Punkt 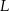 leży na boku
leży na boku 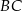 kwadratu
kwadratu 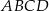 oraz
oraz 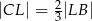 . Punkt
. Punkt 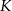 leży na przekątnej
leży na przekątnej 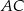 i odcinek
i odcinek 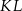 jest prostopadły do
jest prostopadły do 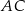 (zobacz rysunek).
(zobacz rysunek).
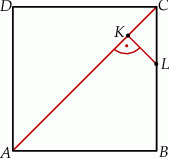
Wykaż, że 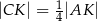 .
.
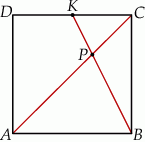
Na boku 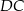 kwadratu
kwadratu 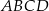 obrano punkt
obrano punkt 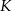 tak, że
tak, że 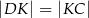 . Przekątna
. Przekątna 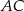 kwadratu przecina odcinek
kwadratu przecina odcinek 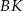 w punkcie
w punkcie 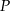 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 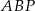 jest czterokrotnie większe niż pole trójkąta
jest czterokrotnie większe niż pole trójkąta 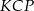 .
.
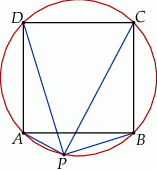
Punkt 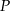 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 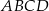 . Wykaż, że
. Wykaż, że 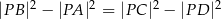 .
.
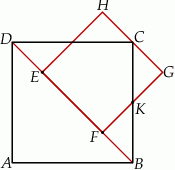
Na rysunku przedstawiono dwa kwadraty: 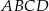 i
i 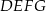 , przy czym punkty
, przy czym punkty 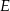 i
i 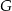 należą do odcinków
należą do odcinków 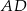 i
i 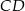 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 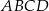 i przechodzi przez punkt
i przechodzi przez punkt 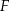 . Wykaż, że jeżeli
. Wykaż, że jeżeli 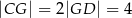 , to promień okręgu jest równy
, to promień okręgu jest równy 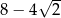 .
.
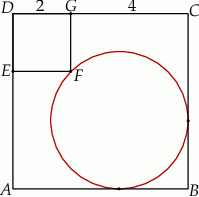
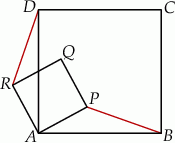
Czworokąty 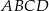 i
i 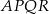 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 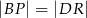 .
.
Na zewnątrz kwadratu 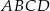 na bokach
na bokach 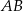 i
i 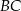 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 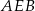 i
i 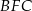 . Uzasadnij, że proste
. Uzasadnij, że proste 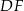 i
i 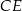 są prostopadłe.
są prostopadłe.