W tabeli przedstawiono roczne przyrosty wysokości pewnej sosny w ciągu sześciu kolejnych lat.
| kolejne lata | 1 | 2 | 3 | 4 | 5 | 6 |
| przyrost (w cm) | 10 | 10 | 7 | 8 | 8 | 7 |
Oblicz średni roczny przyrost wysokości tej sosny w badanym okresie sześciu lat. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia. Podaj ten błąd w procentach.


 .
. 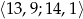 .
. 
 ocen bardzo dobrych (5) z matematyki wystawionych na koniec semestru w tej klasie.
ocen bardzo dobrych (5) z matematyki wystawionych na koniec semestru w tej klasie. 
 ocen dobrych (4) otrzymanych przez uczniów na tym sprawdzianie.
ocen dobrych (4) otrzymanych przez uczniów na tym sprawdzianie. 