Określ liczbę pierwiastków równania 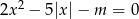 w zależności od wartości parametru
w zależności od wartości parametru 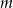 .
.
/Szkoła średnia/Równania/Z wartością bezwględną/Liniowe/Z parametrem
Dla jakich wartości parametru  równanie
równanie 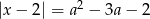 ma dwa pierwiastki różnych znaków?
ma dwa pierwiastki różnych znaków?
Dla jakich wartości parametru 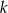 równanie
równanie 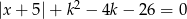 ma dwa pierwiastki różnych znaków?
ma dwa pierwiastki różnych znaków?
Wyznacz wszystkie wartości parametru 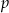 , dla których równanie
, dla których równanie 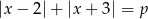 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 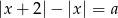 nie ma rozwiązania.
nie ma rozwiązania.
Zbadaj dla jakich wartości parametru 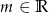 równanie
równanie 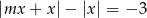 ma rozwiązanie.
ma rozwiązanie.
Wyznacz te wartości parametru 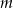 , dla których równanie
, dla których równanie 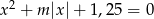 ma cztery rozwiązania.
ma cztery rozwiązania.
Wyznacz wszystkie wartości parametru 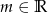 , dla których równanie
, dla których równanie 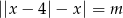 ma tylko jedno rozwiązanie.
ma tylko jedno rozwiązanie.
Wyznacz wszystkie wartości parametru 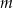 , dla których równanie
, dla których równanie
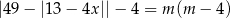
ma cztery różne rozwiązania, których iloczyn jest ujemny.
Zbadaj dla jakich wartości parametru 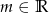 równanie
równanie 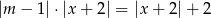 ma rozwiązanie.
ma rozwiązanie.
Podaj liczbę rozwiązań równania 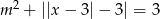 w zależności od wartości parametru
w zależności od wartości parametru 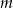 .
.
Wyznacz wszystkie wartości parametru 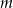 , dla których wśród rozwiązań równania
, dla których wśród rozwiązań równania
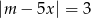
są zarówno liczby dodatnie, jak i ujemne.
Dla jakich wartości parametru 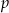 równanie
równanie 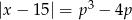 ma dwa rozwiązania, których iloczyn jest liczbą dodatnią?
ma dwa rozwiązania, których iloczyn jest liczbą dodatnią?
Dla jakich wartości parametru  równanie
równanie 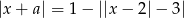 ma dokładnie 2 rozwiązania?
ma dokładnie 2 rozwiązania?
Dla jakich wartości parametru 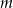 równanie
równanie 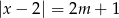 ma jedno rozwiązanie?
ma jedno rozwiązanie?
Dla jakich wartości parametru 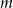 równanie
równanie 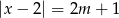 ma dwa rozwiązania?
ma dwa rozwiązania?
Wyznacz te wartości parametru 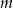 , dla których równanie
, dla których równanie
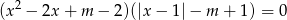
ma dokładnie trzy pierwiastki rzeczywiste? Oblicz te pierwiastki.
Dla jakich wartości parametru 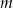 , równanie
, równanie 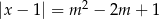 ma dwa pierwiastki dodatnie?
ma dwa pierwiastki dodatnie?
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 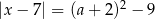 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 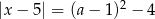 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Zbadaj dla jakich wartości parametru 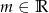 równanie
równanie 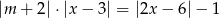 ma rozwiązanie.
ma rozwiązanie.
Dla jakich wartości parametru  równanie
równanie 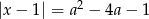 ma dwa dodatnie pierwiastki?
ma dwa dodatnie pierwiastki?
Dla jakich wartości parametru 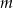 równanie
równanie 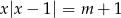 ma dwa różne rozwiązania?
ma dwa różne rozwiązania?

