W ostrosłupie 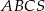 podstawa
podstawa 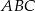 jest trójkątem prostokątnym,
jest trójkątem prostokątnym, 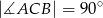 . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość
. Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość 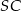 ostrosłupa ma długość 24 cm. Oblicz:
ostrosłupa ma długość 24 cm. Oblicz:
- objętość ostrosłupa;
- tangens kąta nachylenia ściany bocznej ostrosłupa, zawierającej przeciwprostokątną podstawy, do płaszczyzny podstawy.

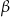 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 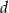 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 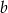 , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę
, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.  i przeciwprostokątnej długości
i przeciwprostokątnej długości  . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
. Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 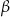 . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe
. Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe 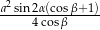 .
. 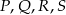 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 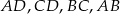 czworościanu
czworościanu 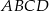 . Wykaż, że punkty
. Wykaż, że punkty 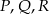 i
i 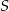 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku. 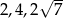 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 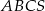 o wierzchołku
o wierzchołku 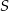 mają długość
mają długość 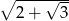 . Wiedząc, że
. Wiedząc, że 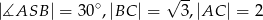 oblicz objętość tego ostrosłupa.
oblicz objętość tego ostrosłupa. 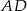 podstawy
podstawy 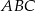 ostrosłupa trójkątnego
ostrosłupa trójkątnego 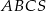 wybrano punkty
wybrano punkty 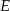 i
i 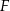 w ten sposób, że
w ten sposób, że 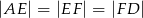 . Przez punkty
. Przez punkty 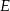 i
i 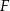 poprowadzono płaszczyzny równoległe do ściany
poprowadzono płaszczyzny równoległe do ściany 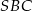 . Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa.
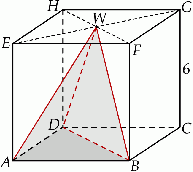
. Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa. 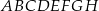 o krawędzi długości 6. Wierzchołki
o krawędzi długości 6. Wierzchołki 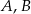 i
i 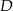 podstawy
podstawy 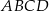 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem  , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy  . Otrzymano w ten sposób ostrosłup trójkątny
. Otrzymano w ten sposób ostrosłup trójkątny  .
. 
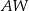 i
i 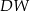 ostrosłupa.
ostrosłupa. 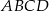 krawędź
krawędź 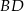 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4. 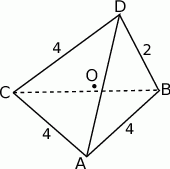
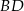 od krawędzi
od krawędzi 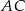 .
. 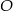 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 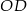 .
.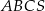 jest trójkąt równoboczny
jest trójkąt równoboczny 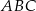 o boku długości 8. Punkt
o boku długości 8. Punkt 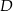 jest środkiem krawędzi
jest środkiem krawędzi 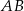 , odcinek
, odcinek 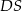 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 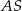 i
i 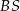 mają długość 7. Oblicz długość krawędzi
mają długość 7. Oblicz długość krawędzi 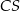 tego ostrosłupa.
tego ostrosłupa. 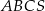 jest trójkąt równoboczny
jest trójkąt równoboczny 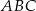 o boku długości 6. Punkt
o boku długości 6. Punkt 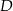 jest środkiem krawędzi
jest środkiem krawędzi 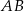 , odcinek
, odcinek 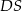 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 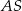 i
i 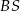 mają długość
mają długość 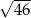 . Oblicz długość krawędzi
. Oblicz długość krawędzi 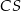 tego ostrosłupa.
tego ostrosłupa. 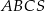 jest trójkąt równoboczny
jest trójkąt równoboczny 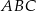 o boku długości 6. Punkt
o boku długości 6. Punkt 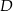 jest środkiem krawędzi
jest środkiem krawędzi 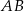 , odcinek
, odcinek 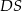 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 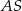 i
i 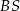 mają długość 8. Oblicz długość krawędzi
mają długość 8. Oblicz długość krawędzi 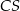 tego ostrosłupa.
tego ostrosłupa. 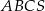 podstawa
podstawa 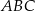 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Krawędź
. Krawędź 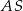 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 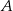 od ściany
od ściany 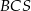 jest równa
jest równa 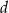 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa. 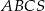 , którego siatkę przedstawiono na rysunku.
, którego siatkę przedstawiono na rysunku. 
 i
i 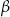 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 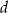 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze 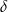 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 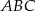 jest podstawą ostrosłupa
jest podstawą ostrosłupa 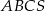 . Punkt
. Punkt 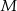 jest środkiem boku
jest środkiem boku 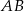 i
i 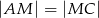 . Odcinek
. Odcinek 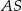 jest wysokością tego ostrosłupa. Wykaż, że kąt
jest wysokością tego ostrosłupa. Wykaż, że kąt 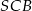 jest prosty.
jest prosty. 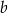 , a kąt między równymi bokami podstawy ma miarę
, a kąt między równymi bokami podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 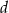 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 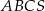 jest trójkąt równoramienny
jest trójkąt równoramienny 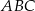 , w którym
, w którym 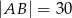 ,
, 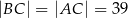 . Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka
. Spodek wysokości ostrosłupa należy do jego podstawy, a każda wysokość ściany bocznej poprowadzona z wierzchołka 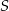 ma długość 26. Oblicz objętość tego ostrosłupa.
ma długość 26. Oblicz objętość tego ostrosłupa. 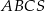 jest trójkąt równoramienny
jest trójkąt równoramienny 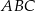 , w którym
, w którym 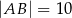 ,
, 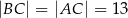 i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka
i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka 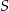 ma długość
ma długość 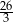 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 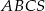 jest trójkąt równoramienny
jest trójkąt równoramienny 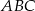 , w którym
, w którym 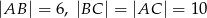 , a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt
, a wszystkie krawędzie boczne tworzą z płaszczyzną podstawy kąt 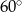 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 