W okrąg o promieniu 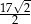 wpisano czworokąt
wpisano czworokąt 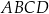 tak, że
tak, że 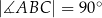 oraz
oraz 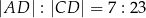 . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 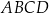 jeżeli jego pole jest równe 192.
jeżeli jego pole jest równe 192.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Oblicz długość...
Długości boków czworokąta 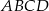 są równe:
są równe: 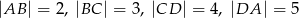 . Na czworokącie
. Na czworokącie 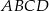 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 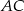 tego czworokąta.
tego czworokąta.
Długości boków czworokąta 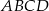 są równe:
są równe: 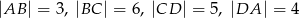 . Na czworokącie
. Na czworokącie 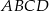 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 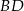 tego czworokąta.
tego czworokąta.
W czworokącie 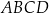 dane są długości boków:
dane są długości boków: 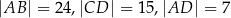 . Ponadto kąty
. Ponadto kąty 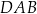 oraz
oraz 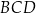 są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
są proste. Oblicz pole tego czworokąta oraz długości jego przekątnych.
Dany jest czworokąt o kolejnych bokach długości 3,4,5 oraz kącie  między bokami długości 3 i 4 takim, że
między bokami długości 3 i 4 takim, że 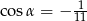 . Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
. Wyznacz długość czwartego boku, jeśli wiadomo, że na czworokącie można opisać okrąg.
Czworokąt 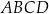 , w którym
, w którym 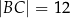 i
i 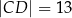 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 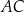 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 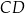 kąt, którego tangens jest równy
kąt, którego tangens jest równy 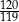 . Tangens kąta
. Tangens kąta 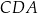 jest równy
jest równy 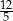 . Oblicz długość odcinka
. Oblicz długość odcinka 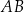 .
.
Wierzchołki rombu 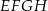 leżą na bokach trójkąta
leżą na bokach trójkąta 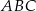 , przy czym boki
, przy czym boki 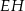 i
i 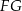 są równoległe do środkowej
są równoległe do środkowej 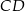 trójkąta
trójkąta 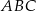 (zobacz rysunek).
(zobacz rysunek).
Oblicz długość boku rombu  jeżeli
jeżeli 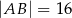 i
i 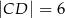 .
.
Przekątne czworokąta wypukłego 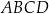 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 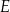 tak, że
tak, że 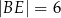 ,
, 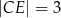 i
i 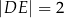 . Ponadto
. Ponadto 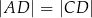 (zobacz rysunek).
(zobacz rysunek).

Oblicz długości boków czworokąta 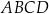 oraz promień opisanego na nim okręgu.
oraz promień opisanego na nim okręgu.
Czworokąt 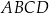 , w którym
, w którym 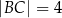 i
i 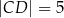 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 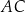 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 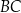 kąt o mierze
kąt o mierze 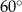 , natomiast z bokiem
, natomiast z bokiem 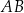 – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy  . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 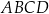 .
.
Czworokąt 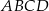 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 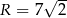 . Kąt
. Kąt 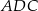 tego czworokąta jest ostry i jego miara jest o
tego czworokąta jest ostry i jego miara jest o 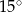 większa od miary kąta
większa od miary kąta 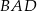 . Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta
. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta 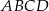 jest równy
jest równy  . Oblicz długości przekątnych
. Oblicz długości przekątnych 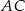 i
i 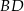 tego czworokąta.
tego czworokąta.
Czworokąt wypukły 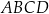 jest wpisany w okrąg o promieniu 4. Kąty
jest wpisany w okrąg o promieniu 4. Kąty 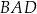 i
i 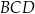 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 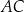 i
i 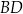 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 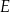 tak, że
tak, że 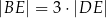 oraz
oraz 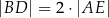 .
.

Oblicz długości boków czworokąta 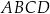 .
.
Czworokąt wypukły 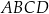 jest wpisany w okrąg o promieniu 9. Kąty
jest wpisany w okrąg o promieniu 9. Kąty 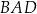 i
i 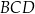 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 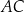 i
i 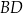 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 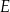 tak, że
tak, że  oraz
oraz 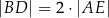 .
.

Oblicz długości boków czworokąta 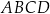 .
.
W czworokąt 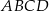 , w którym
, w którym 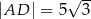 i
i 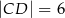 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 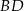 tworzy z bokiem
tworzy z bokiem 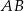 czworokąta kąt o mierze
czworokąta kąt o mierze 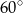 , natomiast z bokiem
, natomiast z bokiem 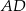 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy  . Wyznacz długości boków
. Wyznacz długości boków 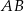 i
i 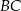 oraz długość przekątnej
oraz długość przekątnej 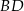 tego czworokąta.
tego czworokąta.
Przekątna 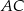 czworokąta
czworokąta 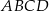 tworzy z bokiem
tworzy z bokiem 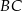 kąt
kąt 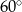 , a z bokiem
, a z bokiem 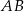 kąt
kąt 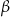 taki, że
taki, że 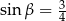 . Promień okręgu opisanego na trójkącie
. Promień okręgu opisanego na trójkącie 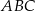 ma długość 5, a bok
ma długość 5, a bok 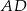 długość
długość 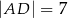 . Wiedząc, że w czworokąt
. Wiedząc, że w czworokąt 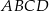 można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej
można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej 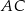 .
.
Na okręgu jest opisany czworokąt 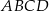 . Bok
. Bok 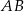 tego czworokąta jest trzy razy krótszy od przekątnej
tego czworokąta jest trzy razy krótszy od przekątnej 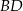 , a bok
, a bok 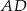 ma długość 10. Ponadto spełnione są następujące warunki:
ma długość 10. Ponadto spełnione są następujące warunki:
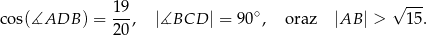
Oblicz długość boku 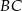 tego czworokąta.
tego czworokąta.
W czworokąt 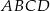 , w którym
, w którym 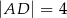 i
i 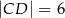 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 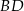 tworzy z bokiem
tworzy z bokiem 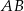 czworokąta kąt o mierze
czworokąta kąt o mierze 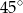 , natomiast z bokiem
, natomiast z bokiem 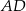 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy 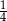 . Wyznacz długości boków
. Wyznacz długości boków 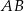 i
i 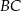 oraz długość przekątnej
oraz długość przekątnej 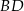 tego czworokąta.
tego czworokąta.
Na okręgu jest opisany czworokąt 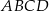 . Bok
. Bok 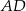 tego czworokąta jest dwa razy dłuższy od boku
tego czworokąta jest dwa razy dłuższy od boku 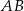 , a przekątna
, a przekątna 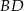 ma długość równą 6. Ponadto spełnione są następujące warunki:
ma długość równą 6. Ponadto spełnione są następujące warunki:
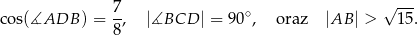
Oblicz długość boku 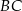 tego czworokąta.
tego czworokąta.
Na czworokącie 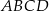 można opisać okrąg. Długości boków tego czworokąta są równe
można opisać okrąg. Długości boków tego czworokąta są równe 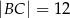 ,
, 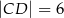 ,
, 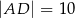 , a kąt
, a kąt 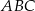 ma miarę
ma miarę 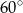 . Oblicz długość promienia okręgu opisanego na czworokącie
. Oblicz długość promienia okręgu opisanego na czworokącie 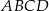 .
.
Czworokąt  , w którym
, w którym 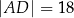 i
i 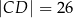 , jest opisany na okręgu. Kąt
, jest opisany na okręgu. Kąt 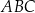 tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie
tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie 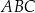 jest równy 12,5. Obwód czworokąta
jest równy 12,5. Obwód czworokąta 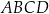 jest równy 66. Oblicz długość przekątnej
jest równy 66. Oblicz długość przekątnej 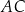 tego czworokąta.
tego czworokąta.
Obwód czworokąta wypukłego 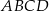 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 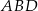 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 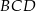 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 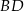 .
.
Czworokąt 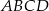 jest wpisany w okrąg. Dane są
jest wpisany w okrąg. Dane są 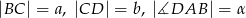 . Wyznacz długość przekątnej
. Wyznacz długość przekątnej 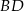 .
.

