Ze zbioru wszystkich liczb trzycyfrowych losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 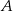 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość
Ze zbioru 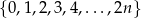 gdzie
gdzie 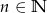 wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi
wylosowano jednocześnie 3 liczby. Prawdopodobieństwo, że suma wylosowanych liczb jest nieparzysta wynosi 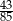 . Wyznacz ile liczb było w zbiorze.
. Wyznacz ile liczb było w zbiorze.
Ze zbioru liczb 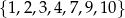 losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
losujemy dwie liczby (mogą się powtarzać). Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest parzysta.
Dany jest pięcioelementowy zbiór 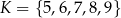 . Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru
. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru 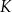 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia 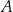 polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.
Ze zbioru 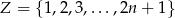 , gdzie
, gdzie 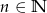 wylosowano równocześnie dwie liczby. Wyznacz
wylosowano równocześnie dwie liczby. Wyznacz  , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od
, tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 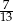 .
.
Spośród liczb 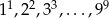 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
Ze zbioru 99 kolejnych liczb naturalnych – od 1 do 99 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 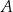 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia 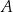 .
.
Liczby 1, 2, 3, 4, 5, 6, 7, 8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że w tym ustawieniu suma każdych dwóch sąsiednich liczb będzie nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru 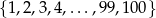 wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru pięciu liczb 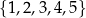 losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 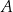 polegającego na tym, że obie wylosowane liczby są nieparzyste.
polegającego na tym, że obie wylosowane liczby są nieparzyste.
Ze zbioru liczb: 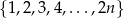 , gdzie
, gdzie 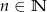 i
i 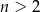 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 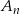 oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a
oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a 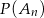 prawdopodobieństwo zajścia zdarzenia
prawdopodobieństwo zajścia zdarzenia 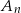 . Oblicz:
. Oblicz: 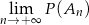 .
.
Ze zbioru liczb 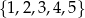 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 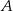 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Ze zbioru liczb 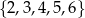 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 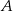 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Ze zbioru liczb 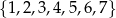 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 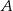 polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
Ze zbioru 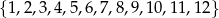 losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?
losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?
Spośród liczb dwucyfrowych wybrano bez zwracania dwa razy po jednej liczbie. Oblicz prawdopodobieństwo, że dwa razy wybrano liczbę parzystą.
Spośród dodatnich liczb dwucyfrowych losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo wylosowania dwóch liczb parzystych.
Ze zbioru liczb 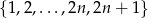 ,
, 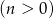 , losujemy jednocześnie dwie liczby. Niech
, losujemy jednocześnie dwie liczby. Niech 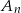 oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.
oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.

