Właściciel sklepu z zabawkami przeprowadził lokalne badanie rynkowe dotyczące wpływu zmiany ceny zestawu klocków na liczbę kupujących ten produkt. Z badania wynika, że dzienny przychód 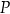 ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o
ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o  zł, wyraża się wzorem
zł, wyraża się wzorem
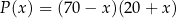
gdzie  jest liczbą całkowitą spełniającą warunki
jest liczbą całkowitą spełniającą warunki 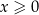 i
i 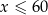 . Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba
. Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba  jest równa
jest równa
A) 25 B) 30 C) 45 D) 50 E) 60

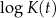 , gdzie
, gdzie 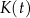 jest liczbą bakterii w próbce po czasie
jest liczbą bakterii w próbce po czasie 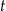 wyrażonym w godzinach, jaki upłynął od chwili
wyrażonym w godzinach, jaki upłynął od chwili 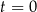 rozpoczęcia obserwacji.
rozpoczęcia obserwacji. 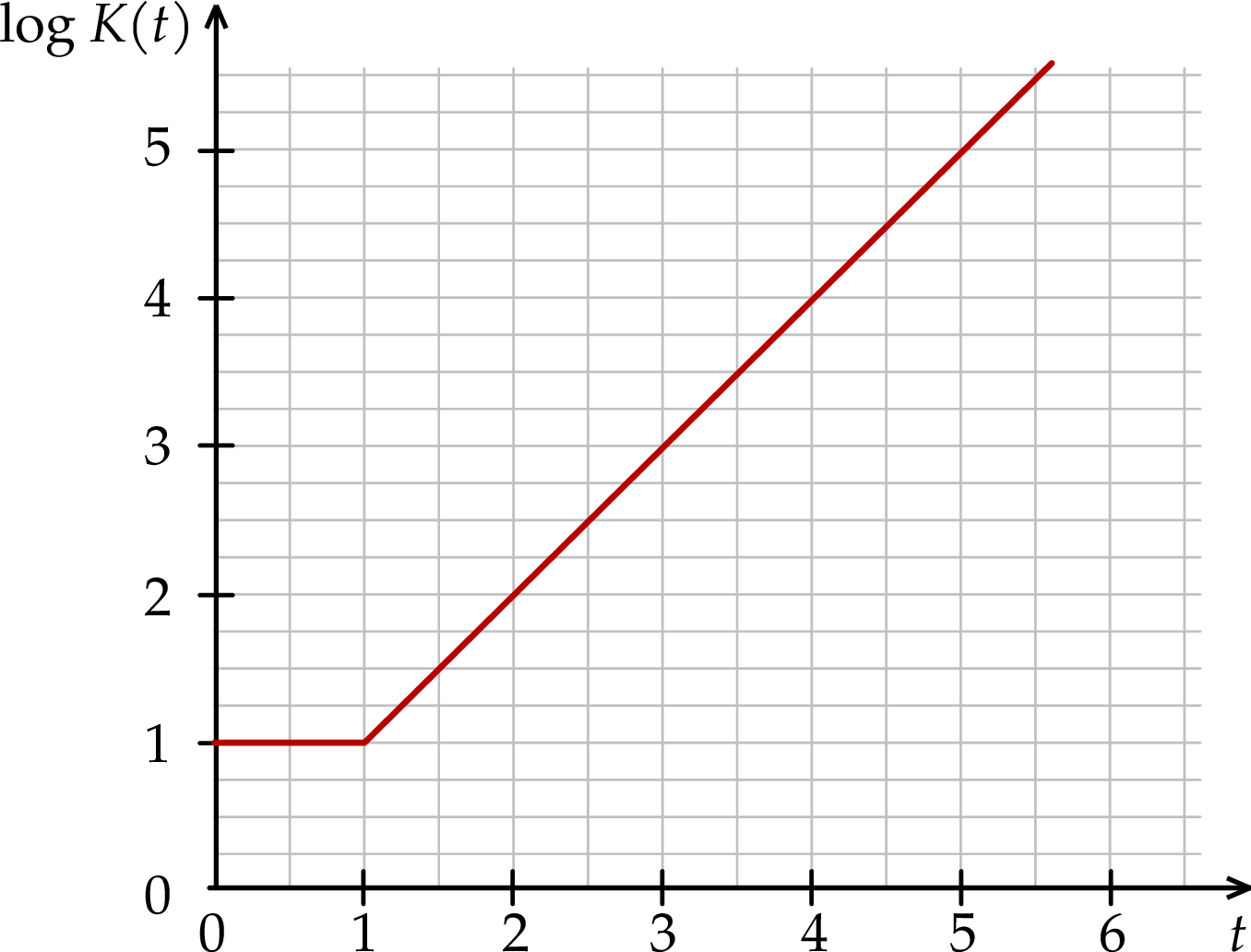
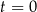 , liczba
, liczba 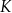 bakterii była równa
bakterii była równa 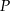 swojego produktu na liczbę
swojego produktu na liczbę 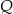 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór 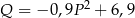
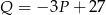
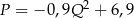
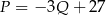
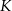 swojego produktu w zależności od liczby
swojego produktu w zależności od liczby 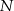 wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór
wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór 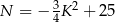
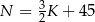
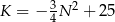
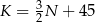
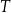 połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder
połowicznego rozpadu izotopu promieniotwórczego to czas, po którym liczba jąder danego izotopu (a zatem i masa tego izotopu) zmniejsza się o połowę – tzn. połowa jąder danego izotopu przemienia się w inne jądra. Liczba jąder 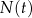 izotopu promieniotwórczego pozostających w próbce po czasie
izotopu promieniotwórczego pozostających w próbce po czasie 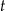 , licząc od chwili
, licząc od chwili 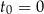 , wyraża się zależnością wykładniczą:
, wyraża się zależnością wykładniczą: 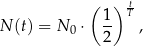
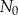 jest liczbą jąder izotopu promieniotwórczego w chwili początkowej
jest liczbą jąder izotopu promieniotwórczego w chwili początkowej 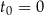 . Wykres zależności wykładniczej
. Wykres zależności wykładniczej 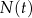 – opisanej we wstępie do zadania – przedstawiono na rysunku
– opisanej we wstępie do zadania – przedstawiono na rysunku 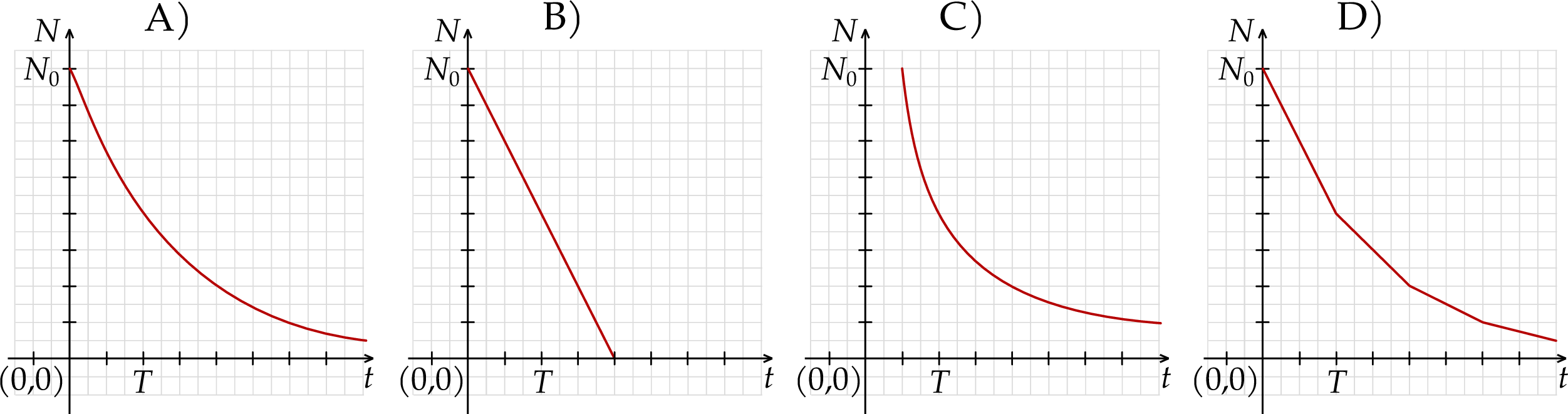
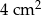 . Gęstość ołowiu jest równa ok.
. Gęstość ołowiu jest równa ok. 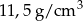 . Masa kostki jest równa około
. Masa kostki jest równa około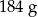
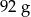
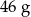
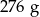
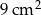 . Gęstość stali jest równa ok.
. Gęstość stali jest równa ok. 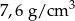 . Masa kostki jest równa około
. Masa kostki jest równa około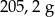
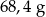
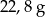
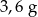
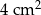 . Gęstość aluminium jest równa ok.
. Gęstość aluminium jest równa ok. 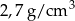 . Masa kostki jest równa około
. Masa kostki jest równa około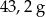
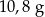
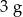
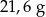
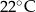 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 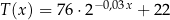 , gdzie
, gdzie 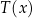 to temperatura naparu wyrażona w stopniach Celsjusza po
to temperatura naparu wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 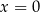 , w którym zioła zalano wrzątkiem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, w którym zioła zalano wrzątkiem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 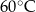 .
. 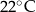 .
. 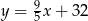 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 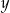 - temperatura w skali Fahrenheita. Zatem 122 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 122 stopnie Fahrenheita są równe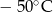
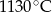
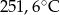
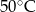
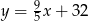 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 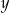 - temperatura w skali Fahrenheita. Zatem 113 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 113 stopnie Fahrenheita są równe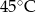
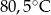
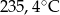
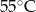
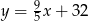 , gdzie
, gdzie  - temperatura w skali Celsjusza,
- temperatura w skali Celsjusza, 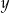 - temperatura w skali Fahrenheita. Zatem 59 stopnie Fahrenheita są równe
- temperatura w skali Fahrenheita. Zatem 59 stopnie Fahrenheita są równe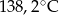
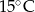
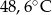
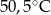
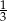 kulek, które pozostały w pudełku. W wyniku tych dwóch operacji liczba kulek w pudełku zmniejszyła się czterokrotnie. Ile kulek było początkowo w pudełku?
kulek, które pozostały w pudełku. W wyniku tych dwóch operacji liczba kulek w pudełku zmniejszyła się czterokrotnie. Ile kulek było początkowo w pudełku?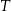 półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa
półtrwania leku w organizmie to czas, po którym masa leku w organizmie zmniejsza się o połowę – po przyjęciu jednorazowej dawki. Przyjmij, że po przyjęciu jednej dawki masa 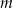 leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą
leku w organizmie zmienia się w czasie zgodnie z zależnością wykładniczą 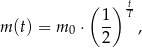
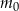 – masa przyjętej dawki leku
– masa przyjętej dawki leku 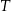 – czas półtrwania leku
– czas półtrwania leku 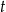 – czas liczony od momentu przyjęcia dawki.
– czas liczony od momentu przyjęcia dawki.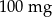 leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę
leku L. Pan Tomasz otrzymuje co 2 dni o godz. 12:00 dawkę 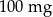 tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy
tego samego leku L. Pierwszą dawkę leku obaj panowie przyjęli tego samego dnia. Czas półtrwania tego leku w organizmie jest równy 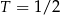 doby.
doby.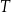 połowicznego rozpadu węgla
połowicznego rozpadu węgla 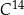 to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla
to czas, po którym względna zawartość tego izotopu w próbce materii organicznej zmniejsza się o połowę. Przyjmij, że czas połowicznego rozpadu węgla 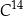 wynosi około
wynosi około 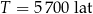 , a pozostała masa tego izotopu wyraża się wzorem
, a pozostała masa tego izotopu wyraża się wzorem 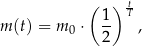
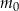 – masa izotopu węgla
– masa izotopu węgla 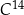 w trakcie życia organizmu
w trakcie życia organizmu 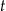 – czas jaki upłynął od czasu śmierci organizmu.
– czas jaki upłynął od czasu śmierci organizmu.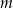 , to masa węgla
, to masa węgla 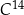 w tej próbce jest równa około
w tej próbce jest równa około 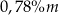
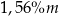
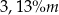
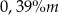
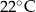 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 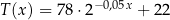 , gdzie
, gdzie 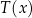 to temperatura naparu wyrażona w stopniach Celsjusza po
to temperatura naparu wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 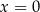 , w którym zioła zalano wrzątkiem. Temperatura naparu po 20 minutach od momentu zalania ziół wrzątkiem jest równa
, w którym zioła zalano wrzątkiem. Temperatura naparu po 20 minutach od momentu zalania ziół wrzątkiem jest równa 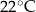
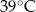
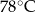
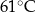
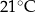 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 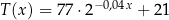 , gdzie
, gdzie 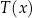 to temperatura herbaty wyrażona w stopniach Celsjusza po
to temperatura herbaty wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 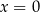 , w którym herbatę zalano wrzątkiem. Temperatura herbaty po 25 minutach od momentu zalania wrzątkiem jest równa
, w którym herbatę zalano wrzątkiem. Temperatura herbaty po 25 minutach od momentu zalania wrzątkiem jest równa 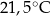
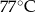
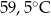
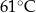
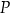 ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o
ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o  zł, wyraża się wzorem
zł, wyraża się wzorem 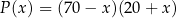
 jest liczbą całkowitą spełniającą warunki
jest liczbą całkowitą spełniającą warunki 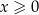 i
i 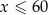 . Dzienny przychód ze sprzedaży zestawów klocków będzie największy, gdy liczba
. Dzienny przychód ze sprzedaży zestawów klocków będzie największy, gdy liczba  jest równa
jest równa 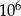
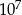
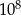
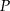 swojego produktu na liczbę
swojego produktu na liczbę 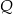 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 6 jednostek powoduje spadek liczby kupujących o 9 jednostek. Ponadto przy cenie równej 9 jednostek liczba kupujących jest równa 24 jednostki. Liczba kupujących ten produkt przy cenie równej 19 jednostek jest równa
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 6 jednostek powoduje spadek liczby kupujących o 9 jednostek. Ponadto przy cenie równej 9 jednostek liczba kupujących jest równa 24 jednostki. Liczba kupujących ten produkt przy cenie równej 19 jednostek jest równa 