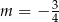Punkty 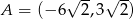 i
i 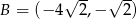 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 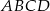 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 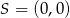 . Środek boku
. Środek boku 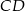 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 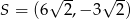 B)
B) 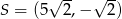 C)
C) 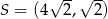 D)
D) 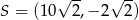
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt/Równoległobok
Punkty 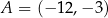 ,
, 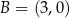 i
i 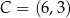 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 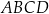 . Wierzchołek
. Wierzchołek 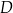 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 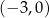 B)
B) 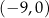 C)
C) 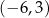 D)
D) 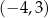
W kartezjańskim układzie współrzędnych  punkty
punkty 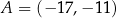 i
i 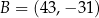 są wierzchołkami równoległoboku
są wierzchołkami równoległoboku 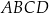 . Punkt
. Punkt 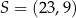 jest środkiem symetrii tego równoległoboku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest środkiem symetrii tego równoległoboku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Równoległobok 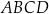 jest rombem. jest rombem. | P | F |
Równoległobok 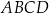 jest prostokątem. jest prostokątem. | P | F |
Punkty 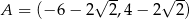 ,
, 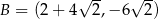 ,
, 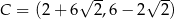 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 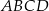 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 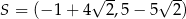 B)
B) 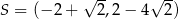
C) 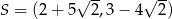 D)
D) 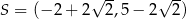
Punkty 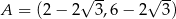 ,
, 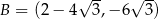 ,
, 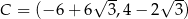 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 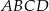 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 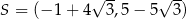 B)
B) 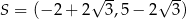
C) 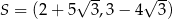 D)
D) 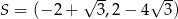
Punkty 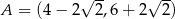 ,
, 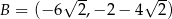 ,
, 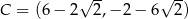 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 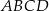 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 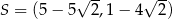 B)
B) 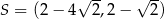
C) 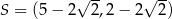 D)
D) 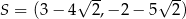
Dane są trzy niewspółliniowe punkty: 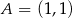 ,
, 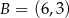 ,
, 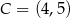 . Ile jest wszystkich punktów
. Ile jest wszystkich punktów 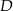 takich, że czworokąt o wierzchołkach w punktach
takich, że czworokąt o wierzchołkach w punktach 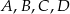 jest równoległobokiem?
jest równoległobokiem?
A) 1 B) 2 C) 3 D) 4
W kartezjańskim układzie współrzędnych  punkt
punkt 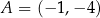 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 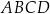 . Punkt
. Punkt 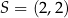 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 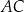 równoległoboku
równoległoboku 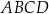 jest równa
jest równa
A) 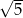 B)
B) 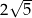 C)
C) 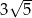 D)
D) 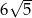
W kartezjańskim układzie współrzędnych 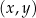 punkt
punkt 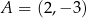 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 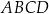 . Punkt
. Punkt 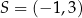 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 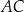 równoległoboku
równoległoboku 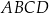 jest równa
jest równa
A) 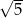 B)
B) 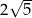 C)
C) 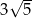 D)
D) 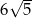
Obwód równoległoboku 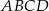 o wierzchołkach
o wierzchołkach 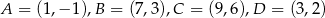 jest równy
jest równy
A) 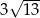 B)
B) 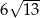 C)
C) 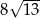 D)
D) 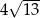
Obwód równoległoboku 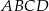 o wierzchołkach
o wierzchołkach 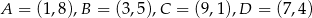 jest równy
jest równy
A) 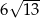 B)
B) 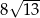 C)
C) 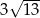 D)
D) 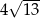
Punkty 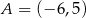 ,
, 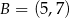 ,
, 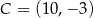 są wierzchołkami równoległoboku
są wierzchołkami równoległoboku 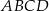 . Długość przekątnej
. Długość przekątnej 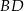 tego równoległoboku jest równa
tego równoległoboku jest równa
A) 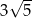 B)
B) 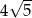 C)
C) 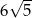 D)
D) 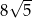
Punkt 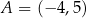 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 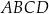 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie 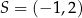 . Wierzchołek
. Wierzchołek 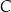 ma współrzędne
ma współrzędne
A) 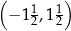 B)
B) 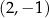 C)
C) 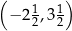 D)
D) 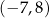
Punkt 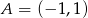 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 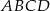 , którego bok
, którego bok 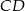 zawiera się w prostej
zawiera się w prostej 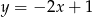 . Podstawa
. Podstawa 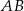 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 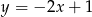 B)
B) 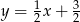 C)
C) 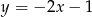 D)
D) 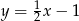
Punkt 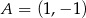 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 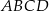 , którego bok
, którego bok 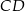 zawiera się w prostej
zawiera się w prostej 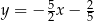 . Podstawa
. Podstawa 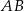 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A)  B)
B) 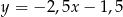 C)
C) 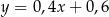 D)
D) 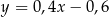
Punkt 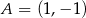 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 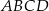 , którego bok
, którego bok 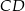 zawiera się w prostej
zawiera się w prostej 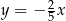 . Podstawa
. Podstawa 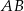 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 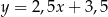 B)
B) 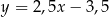 C)
C) 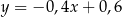 D)
D) 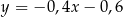
Boki równoległoboku są zawarte w prostych o równaniach: 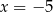 ,
, 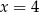 ,
, 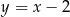 ,
, 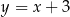 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 45 B) 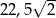 C)
C) 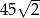 D) 22,5
D) 22,5
Punkty: 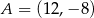 ,
, 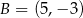 ,
, 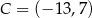 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 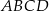 . Wierzchołek
. Wierzchołek 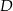 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 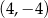 B)
B) 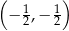 C)
C) 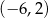 D)
D) 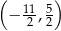
W układzie współrzędnych dany jest równoległobok 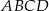 o wierzchołkach
o wierzchołkach 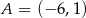 ,
, 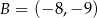 ,
, 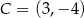 i
i 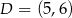 . Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
. Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
A) 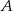 B)
B) 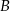 C)
C) 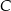 D)
D) 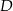
Punkty 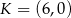 ,
, 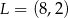 i
i 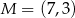 to środki boków, odpowiednio
to środki boków, odpowiednio 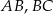 i
i 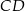 równoległoboku
równoległoboku 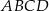 . Różnica długości przekątnych tego równoległoboku jest równa
. Różnica długości przekątnych tego równoległoboku jest równa
A) 4 B) 2 C) 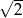 D)
D) 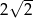
Punkty 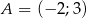 ,
, 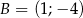 ,
, 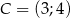 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 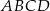 . Równanie prostej zawierającej bok
. Równanie prostej zawierającej bok 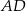 tego równoległoboku ma postać
tego równoległoboku ma postać
A) 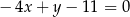 B)
B) 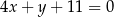
C) 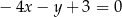 D)
D) 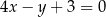
Boki równoległoboku 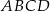 zwierają się w prostych o równaniach:
zwierają się w prostych o równaniach:
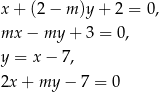
Zatem
A) 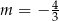 B)
B) 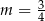 C)
C) 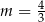 D)
D)