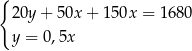Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
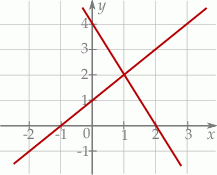
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 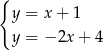 B)
B) 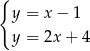 C)
C) 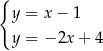 D)
D) 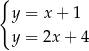
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.

Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 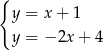 B)
B) 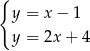 C)
C) 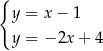 D)
D) 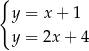
Na rysunku, w kartezjańskim układzie współrzędnych 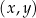 , przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
, przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
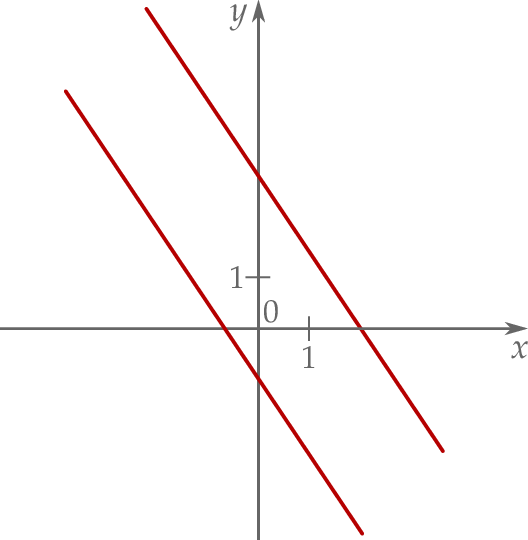
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 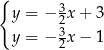 B)
B) 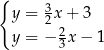
C) 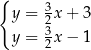 D)
D) 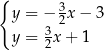
Na rysunku, w kartezjańskim układzie współrzędnych 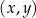 , przedstawiono interpretację geometryczną jednego z poniższych układów równań
, przedstawiono interpretację geometryczną jednego z poniższych układów równań
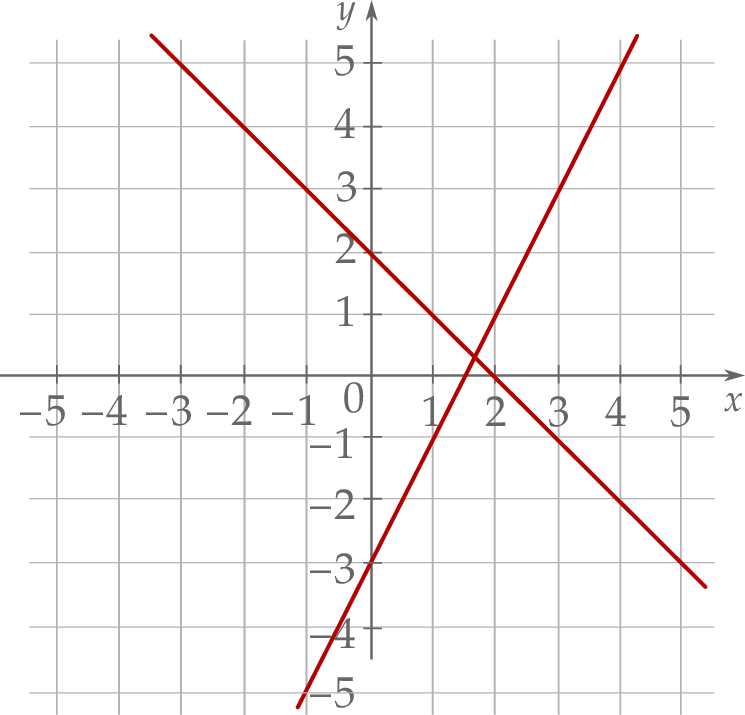
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 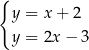 B)
B) 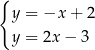 C)
C) 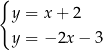 D)
D) 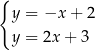
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 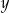 .
.
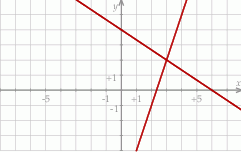
Wskaż ten układ
A) 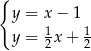 B)
B) 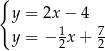 C)
C) 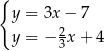 D)
D) 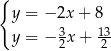
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
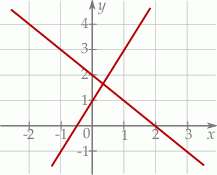
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku.
A) 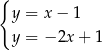 B)
B) 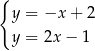 C)
C) 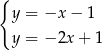 D)
D) 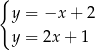
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
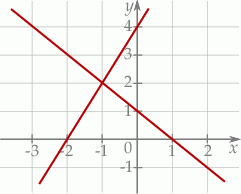
Wskaż ten układ
A) 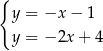 B)
B) 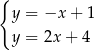 C)
C) 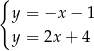 D)
D) 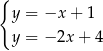
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 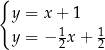 B)
B) 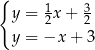 C)
C) 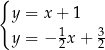 D)
D) 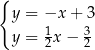
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
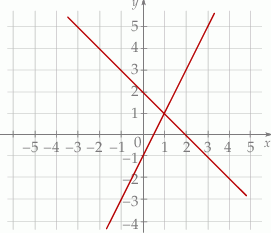
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 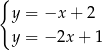 B)
B) 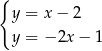 C)
C) 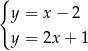 D)
D) 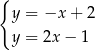
Na rysunku jest przedstawiona graficzna ilustracja układu dwóch równań stopnia pierwszego z dwiema niewiadomymi  i
i 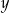 .
.
Wskaż ten układ
A) 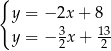 B)
B) 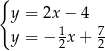 C)
C) 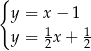 D)
D) 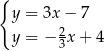
Na rysunku jest przedstawiona graficzna ilustracja układu trzech równań stopnia pierwszego z dwiema niewiadomymi  i
i 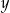 .
.
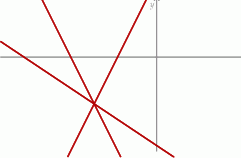
Wskaż ten układ
A) 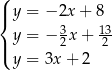 B)
B) 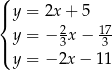 C)
C) 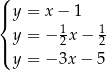 D)
D) 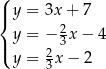
Wybierz równanie, które wraz z równaniem 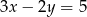 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 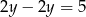 B)
B) 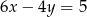 C)
C) 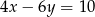 D)
D) 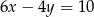
Wybierz równanie, które wraz z równaniem 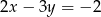 tworzy nieoznaczony układ równań.
tworzy nieoznaczony układ równań.
A) 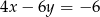 B)
B) 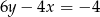 C)
C) 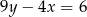 D)
D) 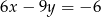
Do sklepu dostarczono  puszek napoju gazowanego o pojemności
puszek napoju gazowanego o pojemności 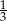 litra oraz
litra oraz 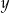 puszek tego napoju o pojemności 0,5 litra. Puszek o mniejszej pojemności było dwa razy więcej niż puszek o pojemności większej. Ponadto w puszkach większych było o 15 litrów napoju mniej niż w puszkach mniejszych. Który układ równań opisuje podane zależności?
puszek tego napoju o pojemności 0,5 litra. Puszek o mniejszej pojemności było dwa razy więcej niż puszek o pojemności większej. Ponadto w puszkach większych było o 15 litrów napoju mniej niż w puszkach mniejszych. Który układ równań opisuje podane zależności?
A) 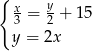 B)
B) 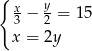 C)
C) 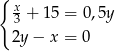 D)
D) 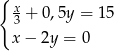
Właściciel sklepu kupił w hurtowni 12 identycznych wiertarek po  zł za sztukę i 15 identycznych szlifierek kątowych po
zł za sztukę i 15 identycznych szlifierek kątowych po  zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki
zł za sztukę. Za zakupy w hurtowni zapłacił 9120 zł. Po doliczeniu marży w wysokości 40 zł do każdej wiertarki i 25% na każdą szlifierkę kątową ceny detaliczne wiertarki i szlifierki były jednakowe. Cenę wiertarki  i szlifierki
i szlifierki  , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 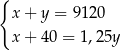 B)
B) 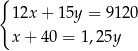
C) 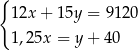 D)
D) 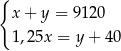
Pięć lat temu ojciec był 3 razy starszy od syna, a za 10 lat będą mieli w sumie 90 lat. Który układ równań opisuje tę sytuację?
A) 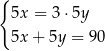 B)
B) 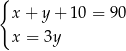
C) 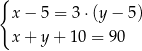 D)
D) 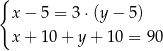
Właściciel sklepu kupił w hurtowni 50 par identycznych spodni po  zł za parę i 40 identycznych marynarek po
zł za parę i 40 identycznych marynarek po 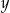 zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni
zł za sztukę. Za zakupy w hurtowni zapłacił 8000 zł. Po doliczeniu marży 50% na każdą parę spodni i 20% na każdą marynarkę ceny detaliczne spodni i marynarki były jednakowe. Cenę pary spodni  oraz cenę marynarki
oraz cenę marynarki 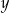 , jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
, jakie trzeba zapłacić w hurtowni, można obliczyć z układu równań
A) 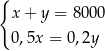 B)
B) 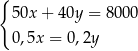 C)
C) 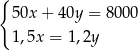 D)
D) 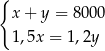
Do sklepu dostarczono  kubłów z farbą o pojemności 10 litrów oraz
kubłów z farbą o pojemności 10 litrów oraz 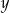 puszek tej farby o pojemności 2 litrów. Puszek było dwa razy więcej niż kubłów. Ponadto w puszkach było o 15 litrów farby mniej niż w kubłach. Który układ równań opisuje podane zależności?
puszek tej farby o pojemności 2 litrów. Puszek było dwa razy więcej niż kubłów. Ponadto w puszkach było o 15 litrów farby mniej niż w kubłach. Który układ równań opisuje podane zależności?
A) 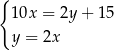 B)
B) 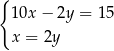
C) 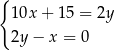 D)
D) 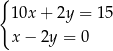
W październiku 2022 roku założono dwa sady, w których posadzono łącznie 1960 drzew. Po roku stwierdzono, że uschło 5% drzew w pierwszym sadzie i 10% drzew w drugim sadzie. Uschnięte drzewa usunięto, a nowych nie dosadzano. Liczba drzew, które pozostały w drugim sadzie, stanowiła 60% liczby drzew, które pozostały w pierwszym sadzie. Niech  oraz
oraz 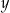 oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby
oznaczają liczby drzew posadzonych – odpowiednio – w pierwszym i drugim sadzie. Układem równań, którego poprawne rozwiązanie prowadzi do obliczenia liczby  drzew posadzonych w pierwszym sadzie oraz liczby
drzew posadzonych w pierwszym sadzie oraz liczby 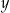 drzew posadzonych w drugim sadzie, jest
drzew posadzonych w drugim sadzie, jest
A) 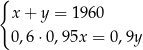 B)
B) 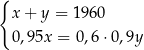
C) 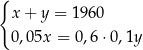 D)
D) 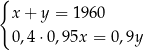
Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości  i
i 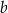 jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 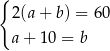 B)
B) 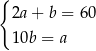 C)
C) 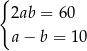 D)
D) 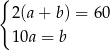
Rozważmy treść następującego zadania:
Pole prostokąta o bokach długości  i
i 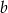 jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 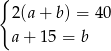 B)
B) 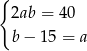 C)
C) 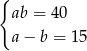 D)
D) 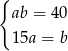
Rozważmy treść następującego zadania:
Obwód rombu o przekątnych długości  i
i 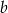 jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
Który układ równań opisuje zależności między długościami przekątnych tego rombu?
A) 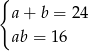 B)
B) 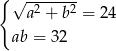 C)
C) 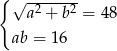 D)
D) 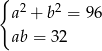
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
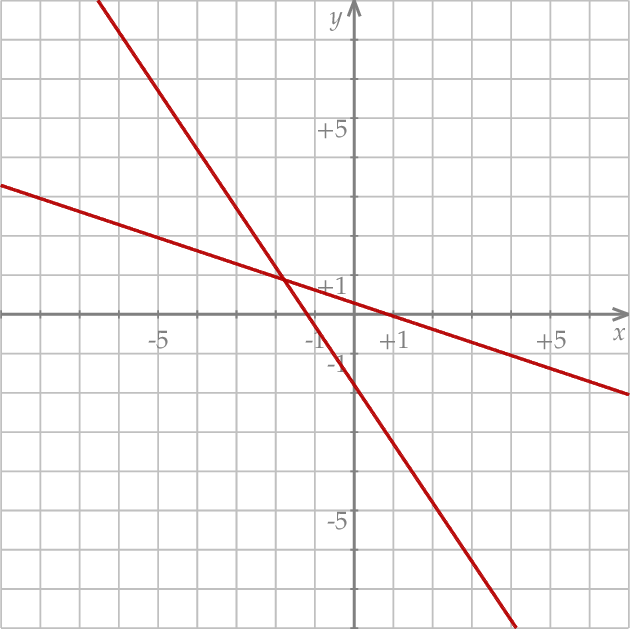
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 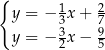 B)
B) 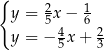 C)
C) 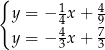 D)
D) 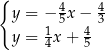
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 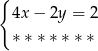 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 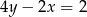 B)
B) 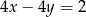 C)
C) 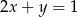 D)
D) 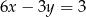
Które z równań należy wpisać w miejsce gwiazdek, aby układ równań 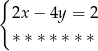 miał nieskończenie wiele rozwiązań?
miał nieskończenie wiele rozwiązań?
A) 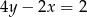 B)
B) 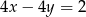 C)
C) 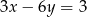 D)
D) 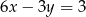
Dane jest równanie 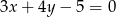 . Z którym z poniższych równań tworzy ono układ sprzeczny?
. Z którym z poniższych równań tworzy ono układ sprzeczny?
A) 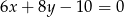 B)
B) 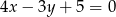 C)
C) 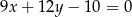 D)
D) 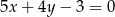
Dane jest równanie 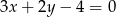 . Z którym z poniższych równań tworzy ono układ sprzeczny?
. Z którym z poniższych równań tworzy ono układ sprzeczny?
A) 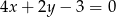 B)
B) 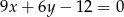 C)
C) 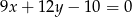 D)
D) 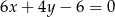
Na rysunku przedstawiono fragmenty dwóch prostych na płaszczyźnie oraz zaznaczono kilka punktów o współrzędnych całkowitych, przez które przechodzą te proste.
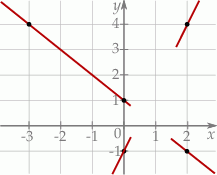
Jeżeli 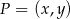 jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
jest punktem wspólnym prostych, których fragmenty przedstawiono na rysunku, to
A) 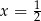 B)
B) 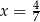 C)
C) 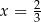 D)
D) 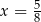
Klient banku wypłacił z bankomatu kwotę 1040 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było dwa razy więcej niż 50–złotowych, a banknotów 20–złotowych było o 2 mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a  – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i  to
to
A) 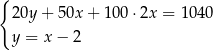 B)
B) 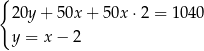
C) 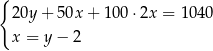 D)
D) 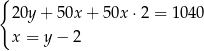
Tomek ma w skarbonce wyłącznie monety dwuzłotowe i pięciozłotowe. W sumie ma w skarbonce 351 zł. Gdyby dołożył do skarbonki 10 monet pięciozłotowych i dwie monety dwuzłotowe, to miałby w skarbonce dwa razy więcej monet dwuzłotowych, niż monet pięciozłotowych. Jeżeli oznaczymy przez  liczbę monet pięciozłotowych, a przez
liczbę monet pięciozłotowych, a przez 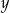 liczbę monet dwuzłotowych w skarbonce Tomka, to liczby
liczbę monet dwuzłotowych w skarbonce Tomka, to liczby  i
i  spełniają układ równań
spełniają układ równań
A) 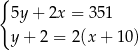 B)
B) 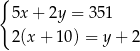
C) 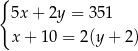 D)
D) 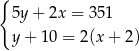
Klient banku wypłacił z bankomatu kwotę 1680 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było o 50% więcej niż 50–złotowych, a banknotów 20–złotowych było o 50% mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 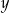 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 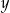 to
to
A) 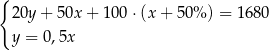 B)
B) 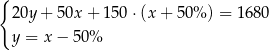
C) 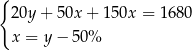 D)
D)