Wierzchołki 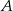 i
i 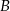 kwadratu
kwadratu 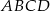 leżą na paraboli
leżą na paraboli 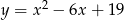 , przy czym odcinek
, przy czym odcinek 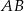 jest równoległy do osi
jest równoległy do osi 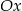 . Wykaż, że jeżeli odległość punktu
. Wykaż, że jeżeli odległość punktu 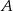 od osi
od osi 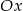 jest liczbą całkowitą to pole kwadratu
jest liczbą całkowitą to pole kwadratu 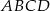 również jest liczbą całkowitą.
również jest liczbą całkowitą.
/Szkoła średnia/Geometria/Geometria analityczna/Parabola
Napisz równanie okręgu, do którego należą punkty wspólne paraboli 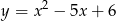 i prostej
i prostej 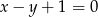 , a którego środek należy do prostej o równaniu
, a którego środek należy do prostej o równaniu 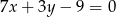 .
.
Punkty 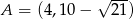 i
i 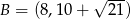 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 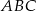 , o kącie prostym przy wierzchołku
, o kącie prostym przy wierzchołku 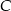 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 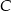 tego trójkąta, wiedząc, że leży on na paraboli o równaniu
tego trójkąta, wiedząc, że leży on na paraboli o równaniu 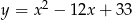 .
.
Wierzchołki trójkąta równobocznego 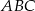 są punktami paraboli
są punktami paraboli 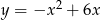 . Punkt
. Punkt 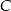 jest jej wierzchołkiem, a bok
jest jej wierzchołkiem, a bok 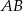 jest równoległy do osi
jest równoległy do osi 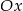 . Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
. Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
Wszystkie wierzchołki trapezu 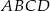 (
(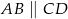 i
i 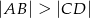 ) leżą na paraboli o równaniu
) leżą na paraboli o równaniu 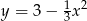 . Wierzchołki
. Wierzchołki 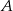 i
i 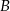 są punktami przecięcia tej paraboli z osią
są punktami przecięcia tej paraboli z osią 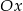 . Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe
. Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe 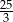 .
.
Dane są parabola o równaniu 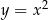 oraz punkty
oraz punkty 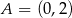 i
i 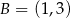 (zobacz rysunek).
(zobacz rysunek).
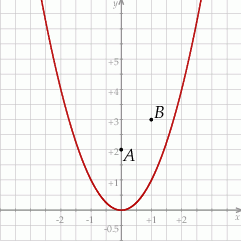
Rozpatrujemy wszystkie trójkąty 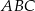 , których wierzchołek
, których wierzchołek 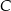 leży na tej paraboli. Niech
leży na tej paraboli. Niech 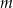 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 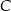 .
.
- Wyznacz pole
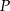 trójkąta
trójkąta 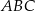 jako funkcję zmiennej
jako funkcję zmiennej 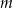 .
. - Wyznacz wszystkie wartości
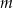 , dla których trójkąt
, dla których trójkąt 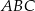 jest ostrokątny.
jest ostrokątny.
Dane są parabola o równaniu 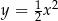 oraz punkty
oraz punkty 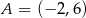 i
i 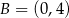 (zobacz rysunek).
(zobacz rysunek).
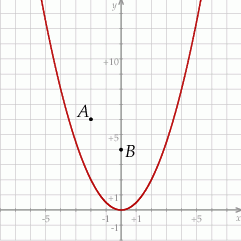
Rozpatrujemy wszystkie trójkąty 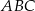 , których wierzchołek
, których wierzchołek 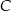 leży na tej paraboli. Niech
leży na tej paraboli. Niech 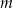 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 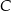 .
.
- Wyznacz pole
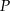 trójkąta
trójkąta 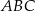 jako funkcję zmiennej
jako funkcję zmiennej 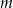 .
. - Wyznacz wszystkie wartości
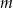 , dla których trójkąt
, dla których trójkąt 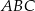 jest ostrokątny.
jest ostrokątny.
Prosta 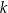 o równaniu
o równaniu 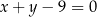 przecina parabolę o równaniu
przecina parabolę o równaniu 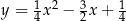 w punktach
w punktach 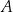 oraz
oraz 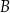 . Pierwsza współrzędna punktu
. Pierwsza współrzędna punktu 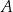 jest liczbą dodatnią; pierwsza współrzędna punktu
jest liczbą dodatnią; pierwsza współrzędna punktu 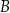 jest liczbą ujemną. Prosta
jest liczbą ujemną. Prosta 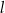 jest równoległa do prostej
jest równoległa do prostej 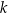 i styczna do danej paraboli w punkcie
i styczna do danej paraboli w punkcie 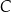 . Oblicz odległość punktu
. Oblicz odległość punktu 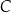 od prostej
od prostej 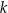 oraz pole trójkąta
oraz pole trójkąta 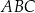 .
.
Prosta 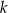 o równaniu
o równaniu 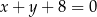 przecina parabolę o równaniu
przecina parabolę o równaniu 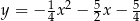 w punktach
w punktach 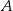 oraz
oraz 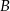 . Pierwsza współrzędna punktu
. Pierwsza współrzędna punktu 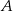 jest liczbą ujemną; pierwsza współrzędna punktu
jest liczbą ujemną; pierwsza współrzędna punktu 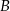 jest liczbą dodatnią. Prosta
jest liczbą dodatnią. Prosta 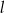 jest równoległa do prostej
jest równoległa do prostej 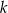 i styczna do danej paraboli w punkcie
i styczna do danej paraboli w punkcie 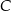 . Oblicz odległość punktu
. Oblicz odległość punktu 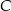 od prostej
od prostej 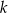 oraz pole trójkąta
oraz pole trójkąta 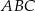 .
.
Oblicz współrzędne punktów przecięcia wykresów funkcji 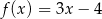 i funkcji
i funkcji 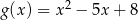 .
.
Jeden z końców odcinka leży na paraboli 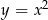 , a drugi na prostej o równaniu
, a drugi na prostej o równaniu 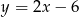 . Wykaż, że długość tego odcinka jest nie mniejsza od
. Wykaż, że długość tego odcinka jest nie mniejsza od 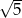 . Sporządź odpowiedni rysunek.
. Sporządź odpowiedni rysunek.
Udowodnij, że każdy punkt paraboli o równaniu 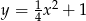 jest równoodległy od osi
jest równoodległy od osi 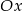 i od punktu
i od punktu 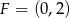 .
.
Dana jest parabola o równaniu 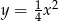 i punkt
i punkt 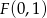 . Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu
. Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu 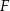 i prostej
i prostej 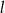 o równaniu
o równaniu 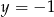 .
.
Punkty przecięcia paraboli 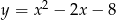 z prostą
z prostą 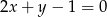 są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
Każdy z wierzchołków trójkąta prostokątnego 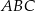 leży na na wykresie funkcji
leży na na wykresie funkcji 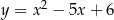 . Bok
. Bok 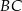 tego trójkąta jest zawarty w prostej
tego trójkąta jest zawarty w prostej 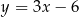 , a wierzchołek
, a wierzchołek 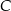 kąta prostego ma obie współrzędne dodatnie. Oblicz pole trójkąta
kąta prostego ma obie współrzędne dodatnie. Oblicz pole trójkąta 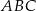 .
.
Rozważmy cięciwy 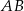 paraboli
paraboli 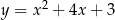 przechodzące przez punkt
przechodzące przez punkt 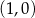 , przy czym przez cięciwę
, przy czym przez cięciwę 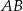 rozumiemy prostą przecinającą tę parabolę w dwóch punktach
rozumiemy prostą przecinającą tę parabolę w dwóch punktach 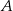 i
i 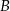 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 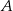 i
i 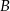 , dla których suma współrzędnych środka odcinka
, dla których suma współrzędnych środka odcinka 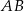 cięciwy
cięciwy 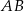 jest równa
jest równa 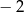 .
.
W kartezjańskim układzie współrzędnych 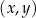 prosta o równaniu
prosta o równaniu 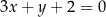 przecina parabolę o równaniu
przecina parabolę o równaniu 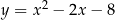 w punktach
w punktach 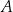 oraz
oraz 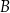 , które są kolejnymi wierzchołkami równoległoboku
, które są kolejnymi wierzchołkami równoległoboku 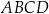 . Wierzchołek
. Wierzchołek 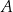 ma pierwszą współrzędną ujemną. Wierzchołek
ma pierwszą współrzędną ujemną. Wierzchołek 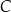 leży na prostej o równaniu
leży na prostej o równaniu 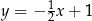 i ma pierwszą współrzędną dodatnią. Odległość punktu
i ma pierwszą współrzędną dodatnią. Odległość punktu 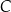 od prostej zawierającej bok
od prostej zawierającej bok 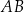 równoległoboku jest równa
równoległoboku jest równa 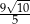 . Oblicz długość boku
. Oblicz długość boku 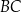 tego równoległoboku.
tego równoległoboku.
W kartezjańskim układzie współrzędnych 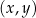 prosta
prosta 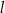 o równaniu
o równaniu 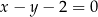 przecina parabolę o równaniu
przecina parabolę o równaniu 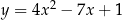 w punktach
w punktach 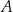 oraz
oraz 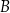 . Odcinek
. Odcinek 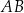 jest średnicą okręgu
jest średnicą okręgu 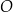 . Punkt
. Punkt 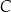 leży na okręgu
leży na okręgu 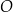 nad prostą
nad prostą 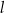 , a kąt
, a kąt 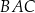 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 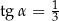 (zobacz rysunek).
(zobacz rysunek).
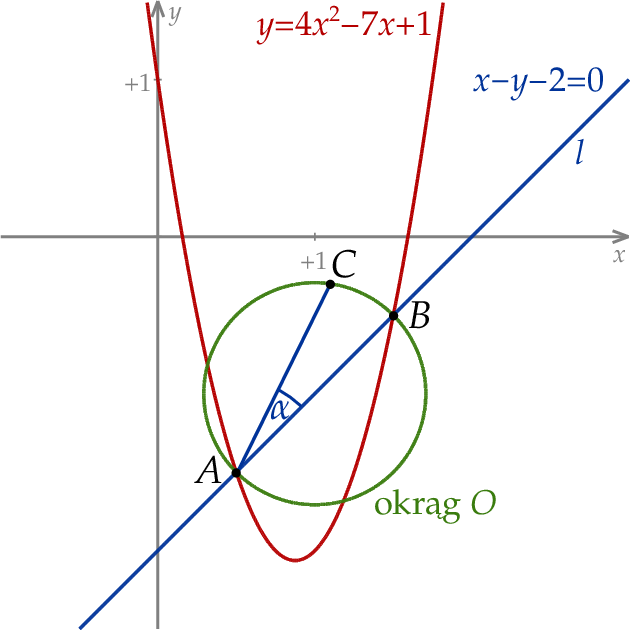
Oblicz współrzędne punktu 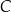 .
.
W kartezjańskim układzie współrzędnych 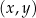 prosta
prosta 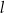 o równaniu
o równaniu 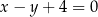 przecina parabolę o równaniu
przecina parabolę o równaniu 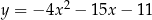 w punktach
w punktach 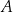 oraz
oraz 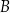 . Odcinek
. Odcinek 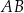 jest średnicą okręgu
jest średnicą okręgu 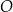 . Punkt
. Punkt 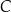 leży na okręgu
leży na okręgu 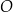 poniżej prostej
poniżej prostej 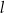 , a kąt
, a kąt 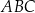 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 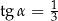 (zobacz rysunek).
(zobacz rysunek).
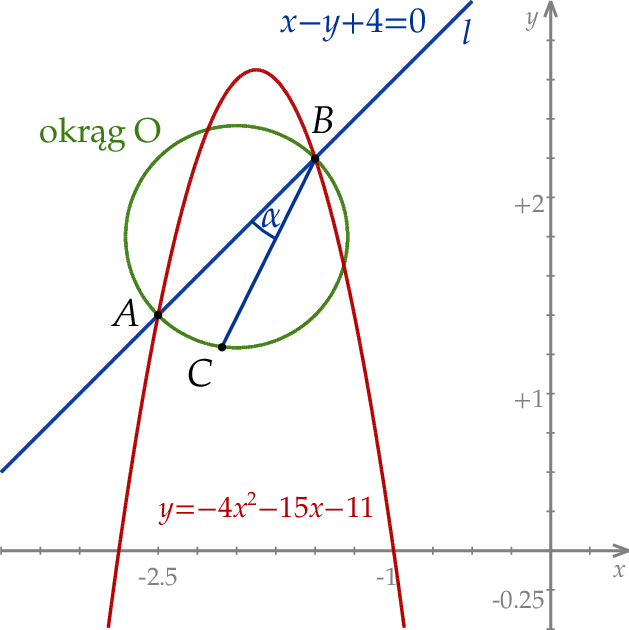
Oblicz współrzędne punktu 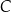 .
.

