W trójkącie 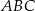 dane są długości boków
dane są długości boków 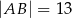 i
i 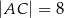 oraz
oraz 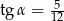 , gdzie
, gdzie 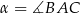 . Oblicz pole trójkąta
. Oblicz pole trójkąta 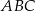 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 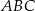 dane są długości boków
dane są długości boków 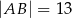 i
i 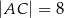 oraz
oraz 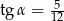 , gdzie
, gdzie 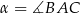 . Oblicz pole trójkąta
. Oblicz pole trójkąta 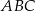 .
.

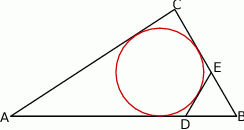
Na bokach 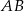 i
i 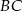 trójkąta
trójkąta 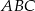 wybrano punkty
wybrano punkty 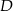 i
i 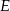 w ten sposób, że odcinek
w ten sposób, że odcinek 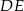 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 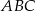 oraz trójkąt
oraz trójkąt 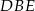 jest równoboczny. Obwód trójkąta
jest równoboczny. Obwód trójkąta 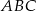 jest równy 20, a długość boku
jest równy 20, a długość boku 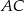 jest równa 7. Oblicz pole trójkąta
jest równa 7. Oblicz pole trójkąta 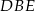 .
.
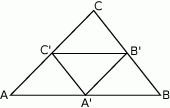
Punkty 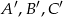 są środkami boków trójkąta
są środkami boków trójkąta 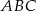 . Pole trójkąta
. Pole trójkąta 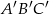 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta 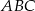 .
.
Punkt 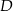 leży na boku
leży na boku 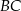 trójkąta
trójkąta 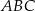 oraz
oraz 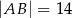 ,
, 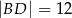 ,
, 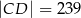 i
i 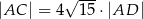 . Oblicz pole trójkąta
. Oblicz pole trójkąta 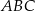 .
.
Na środkowej 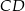 trójkąta
trójkąta 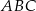 wybrano punkt
wybrano punkt 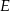 . Wykaż, że trójkąty
. Wykaż, że trójkąty 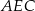 i
i 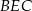 mają równe pola.
mają równe pola.
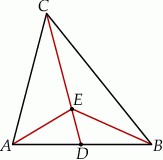
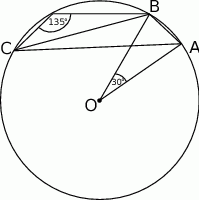
Oblicz pole trójkąta 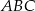 przedstawionego na rysunku, jeśli wiadomo, że
przedstawionego na rysunku, jeśli wiadomo, że 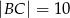 oraz
oraz 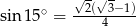 .
.
W trójkącie 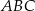 poprowadzono odcinki
poprowadzono odcinki 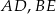 i
i 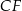 w ten sposób, że punkty
w ten sposób, że punkty 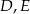 i
i 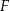 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 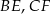 i
i 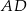 . Oblicz pole trójkąta
. Oblicz pole trójkąta 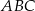 jeżeli pole trójkąta
jeżeli pole trójkąta 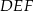 jest równe 2.
jest równe 2.
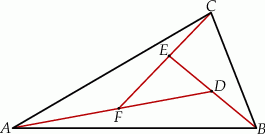
Na dwusiecznej 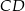 trójkąta
trójkąta 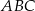 , w którym
, w którym 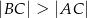 wybrano punkt
wybrano punkt 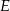 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 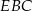 jest większe od pola trójkąta
jest większe od pola trójkąta 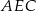 .
.
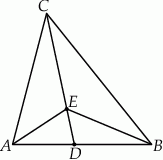
Dany jest trójkąt 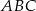 , w którym
, w którym 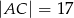 i
i 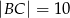 . Na boku
. Na boku 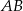 leży punkt
leży punkt 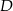 taki, że
taki, że 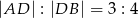 oraz
oraz 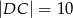 . Oblicz pole trójkąta
. Oblicz pole trójkąta 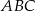 .
.
W trójkącie rozwartokątnym 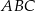 o kącie rozwartym przy wierzchołku
o kącie rozwartym przy wierzchołku 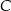 poprowadzono wysokość
poprowadzono wysokość 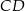 i otrzymano równoramienny trójkąt
i otrzymano równoramienny trójkąt 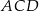 . Długości boków
. Długości boków 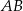 i
i 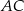 są odpowiednio równe
są odpowiednio równe 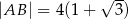 i
i 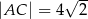 . Oblicz pole powierzchni koła opisanego na trójkącie
. Oblicz pole powierzchni koła opisanego na trójkącie 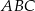 .
.
W trójkącie 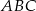 dane są:
dane są: 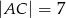 ,
, 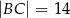 i
i 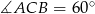 . Oblicz pole trójkąta
. Oblicz pole trójkąta 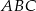 .
.
W trójkącie 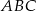 dane są
dane są 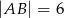 ,
, 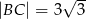 oraz
oraz 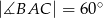 . Oblicz pole trójkąta
. Oblicz pole trójkąta 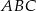 .
.
W trójkącie 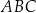 dane są długości boków
dane są długości boków 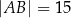 i
i 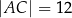 oraz
oraz 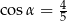 , gdzie
, gdzie 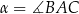 . Na bokach
. Na bokach 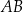 i
i 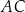 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 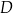 i
i 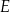 takie, że
takie, że 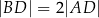 i
i 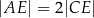 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
trójkąta 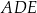 .
.
czworokąta 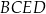 .
.
W trójkącie 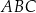 dane są długości boków
dane są długości boków 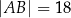 i
i 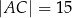 oraz
oraz 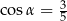 , gdzie
, gdzie 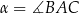 . Na bokach
. Na bokach 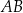 i
i 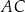 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 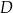 i
i 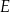 takie, że
takie, że 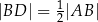 i
i 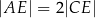 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
trójkąta 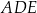 .
.
czworokąta 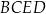 .
.
Wyraź pole trójkąta w zależności od długości jednego z jego boków i miar kątów doń przyległych.
Punkty 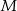 i
i 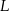 leżą odpowiednio na bokach
leżą odpowiednio na bokach 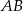 i
i 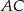 trójkąta
trójkąta 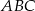 , przy czym zachodzą równości
, przy czym zachodzą równości 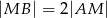 oraz
oraz 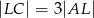 . Punkt
. Punkt 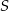 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 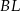 i
i 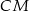 . Punkt
. Punkt 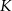 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 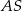 z odcinkiem
z odcinkiem 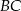 (zobacz rysunek).
(zobacz rysunek).
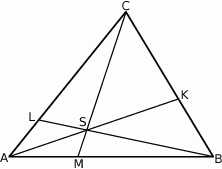
Pole trójkąta 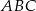 jest równe 660. Oblicz pola trójkątów:
jest równe 660. Oblicz pola trójkątów: 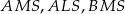 i
i 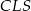 .
.
Punkty 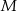 i
i 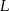 leżą odpowiednio na bokach
leżą odpowiednio na bokach 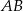 i
i 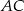 trójkąta
trójkąta 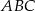 , przy czym zachodzą równości
, przy czym zachodzą równości 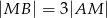 oraz
oraz 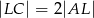 . Punkt
. Punkt 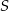 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 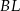 i
i 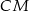 . Punkt
. Punkt 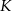 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 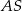 z odcinkiem
z odcinkiem 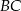 (zobacz rysunek).
(zobacz rysunek).
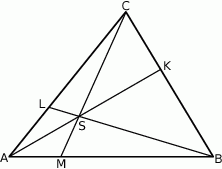
Pole trójkąta 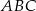 jest równe 528. Oblicz pola trójkątów:
jest równe 528. Oblicz pola trójkątów: 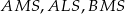 i
i 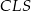 .
.
Na boku 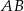 trójkąta
trójkąta 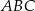 wybrano punkt
wybrano punkt 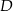 , a na odcinku
, a na odcinku 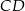 wybrano punkt
wybrano punkt 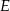 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 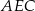 i
i 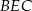 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 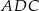 i
i 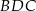 .
.
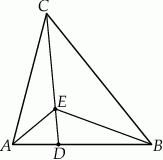
W trójkącie 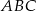 dwa kąty przy wierzchołkach
dwa kąty przy wierzchołkach 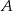 i
i 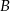 mają odpowiednio miary:
mają odpowiednio miary: 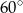 i
i 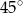 . Oblicz pole tego trójkąta, wiedząc, że długość boku
. Oblicz pole tego trójkąta, wiedząc, że długość boku 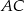 jest równa
jest równa 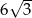 .
.
Dany jest trójkąt 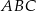 , w którym
, w którym 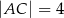 ,
, 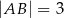 ,
, 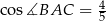 . Oblicz pole trójkąta
. Oblicz pole trójkąta 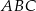 .
.
Dany jest trójkąt 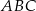 , w którym
, w którym 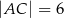 ,
, 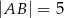 ,
, 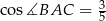 . Oblicz pole trójkąta
. Oblicz pole trójkąta 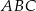 .
.
Dany jest trójkąt 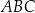 . Na boku
. Na boku 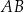 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 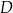 , taki, że
, taki, że 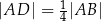 , a na boku
, a na boku 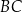 wybrano taki punkt
wybrano taki punkt 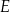 , że
, że 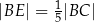 (zobacz rysunek poniżej). Pole trójkąta
(zobacz rysunek poniżej). Pole trójkąta 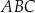 jest równe 20.
jest równe 20.

Oblicz pole trójkąta 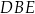 .
.
Trójkąt podzielono odcinkami 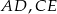 i
i 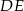 na 5 trójkątów, przy czym
na 5 trójkątów, przy czym 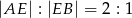 .
.
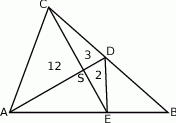
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta  .
.
