Prosta 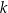 przecina okrąg o środku
przecina okrąg o środku 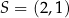 w punktach
w punktach 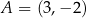 i
i 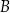 , przy czym
, przy czym 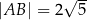 . Wyznacz równanie prostej
. Wyznacz równanie prostej 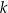 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Punkty wspólne z prostą
Napisz równanie okręgu o środku 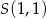 , który na prostej o równaniu
, który na prostej o równaniu 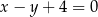 odcina cięciwę
odcina cięciwę 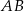 długości
długości 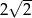 . Wykonaj rysunek.
. Wykonaj rysunek.
Prosta o równaniu 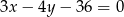 przecina okrąg o środku
przecina okrąg o środku 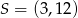 w punktach
w punktach 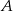 i
i 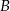 . Długość odcinka
. Długość odcinka 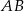 jest równa 40. Wyznacz równanie tego okręgu.
jest równa 40. Wyznacz równanie tego okręgu.
Okrąg o równaniu 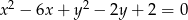 i prosta
i prosta 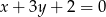 przecinają się w punktach
przecinają się w punktach 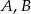 . Wyznacz długość cięciwy
. Wyznacz długość cięciwy 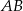 tego okręgu.
tego okręgu.
Dla jakiej wartości 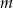 wykres funkcji
wykres funkcji 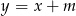 ma co najmniej jeden punkt wspólny z okręgiem o promieniu
ma co najmniej jeden punkt wspólny z okręgiem o promieniu  , którego środkiem jest początek układu współrzędnych?
, którego środkiem jest początek układu współrzędnych?
Końce cięciwy 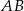 okręgu o równaniu
okręgu o równaniu 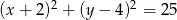 leżą na prostej
leżą na prostej 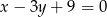 . Oblicz sinus kąta wypukłego
. Oblicz sinus kąta wypukłego 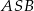 , gdzie
, gdzie 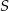 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Wyznacz współrzędne punktów wspólnych prostej 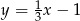 i okręgu
i okręgu 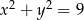 .
.
Wyznacz punkty wspólne okręgu 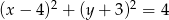 oraz prostej
oraz prostej 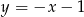 .
.
Oblicz długość cięciwy, którą wycina z prostej 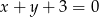 okrąg o środku w punkcie
okrąg o środku w punkcie 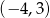 i promieniu 10.
i promieniu 10.
Oblicz długość cięciwy, którą wycina z prostej 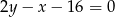 okrąg o środku w punkcie
okrąg o środku w punkcie 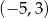 i promieniu 5.
i promieniu 5.
Punkty 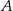 i
i 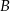 są punktami wspólnymi prostej o równaniu
są punktami wspólnymi prostej o równaniu 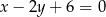 oraz okręgu o środku
oraz okręgu o środku 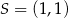 . Długość odcinka
. Długość odcinka 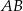 jest równa
jest równa 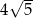 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 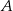 i
i 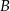 .
.
Środki okręgów 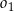 i
i 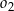 znajdują się po różnych stronach prostej
znajdują się po różnych stronach prostej 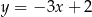 , która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu
, która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu 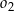 jest równy
jest równy 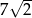 oraz, że okrąg
oraz, że okrąg 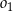 ma równanie
ma równanie 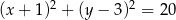 , wyznacz równanie okręgu
, wyznacz równanie okręgu 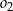 .
.
Dane są okrąg 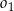 o równaniu
o równaniu 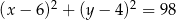 oraz okrąg
oraz okrąg 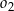 o promieniu
o promieniu 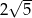 . Środki okręgów
. Środki okręgów 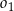 i
i 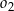 leżą po różnych stronach prostej
leżą po różnych stronach prostej 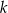 o równaniu
o równaniu 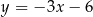 , a punkty wspólne obu okręgów leżą na prostej
, a punkty wspólne obu okręgów leżą na prostej 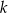 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu 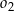 .
.
Wyznacz wszystkie wartości parametru 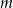 , dla których prosta o równaniu
, dla których prosta o równaniu 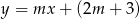 ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie
ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie 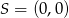 i promieniu
i promieniu 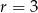 .
.
Ile punktów wspólnych ma okrąg o równaniu 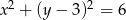 z prostą o równaniu
z prostą o równaniu 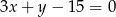 ?
?
Wyznacz wszystkie wartości parametru 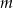 , dla których okrąg o równaniu
, dla których okrąg o równaniu 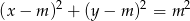 jest styczny do prostej
jest styczny do prostej 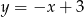 .
.
W układzie współrzędnych punkty 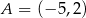 i
i 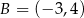 są końcami cięciwy okręgu
są końcami cięciwy okręgu  . Średnica
. Średnica 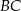 tego okręgu jest zwarta w prostej o równaniu
tego okręgu jest zwarta w prostej o równaniu 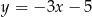 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 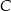 .
.
Ile punktów wspólnych ma prosta 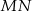 z okręgiem
z okręgiem 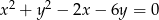 jeśli
jeśli 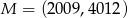 oraz
oraz 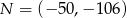 .
.
Określ wzajemne położenie prostej 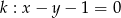 i okręgu o równaniu
i okręgu o równaniu 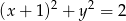 .
.
Prosta 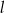 przecina okrąg o środku
przecina okrąg o środku 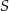 w punktach
w punktach 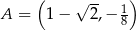 i
i 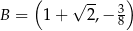 . Punkt
. Punkt 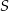 leży na prostej
leży na prostej 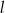 . Oblicz pole koła ograniczonego tym okręgiem.
. Oblicz pole koła ograniczonego tym okręgiem.

