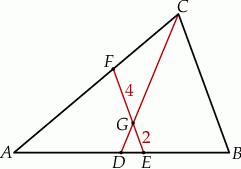
W trójkącie 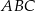 odcinek
odcinek 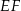 o końcach należących do boków odpowiednio
o końcach należących do boków odpowiednio 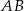 i
i 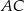 przecina środkową
przecina środkową 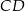 w punkcie
w punkcie 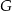 , oraz odcinek
, oraz odcinek 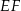 jest równoległy do odcinka
jest równoległy do odcinka 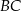 (patrz rysunek). Oblicz długość odcinka
(patrz rysunek). Oblicz długość odcinka 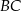 wiedząc, że
wiedząc, że 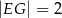 i
i 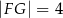 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 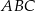 odcinek
odcinek 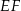 o końcach należących do boków odpowiednio
o końcach należących do boków odpowiednio 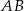 i
i 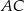 przecina środkową
przecina środkową 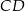 w punkcie
w punkcie 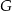 , oraz odcinek
, oraz odcinek 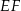 jest równoległy do odcinka
jest równoległy do odcinka 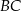 (patrz rysunek). Oblicz długość odcinka
(patrz rysunek). Oblicz długość odcinka 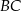 wiedząc, że
wiedząc, że 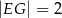 i
i 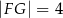 .
.

Okrąg o promieniu 4 jest wpisany w trójkąt. Punkt styczności podzielił jeden z boków na odcinki o długości 6 i 8. Oblicz długości boków tego trójkąta.
W trójkącie 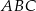 długości boków
długości boków 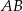 i
i 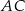 są odpowiednio równe 4 i 6. Punkt
są odpowiednio równe 4 i 6. Punkt 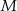 jest środkiem odcinka
jest środkiem odcinka 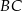 , a długość środkowej
, a długość środkowej 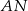 trójkąta
trójkąta 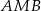 jest równa 3. Oblicz długość boku
jest równa 3. Oblicz długość boku 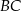 .
.
Promień okręgu opisanego na trójkącie 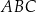 jest równy 17. Najdłuższym bokiem tego trójkąta jest bok
jest równy 17. Najdłuższym bokiem tego trójkąta jest bok 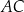 , a długości dwóch pozostałych boków są równe
, a długości dwóch pozostałych boków są równe 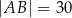 oraz
oraz 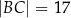 . Oblicz miarę kąta
. Oblicz miarę kąta 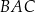 oraz długość boku
oraz długość boku 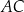 tego trójkąta.
tego trójkąta.
W trójkącie kąt między bokami o długościach 8 i 6 jest równy 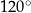 . Jaką długość ma trzeci bok trójkąta?
. Jaką długość ma trzeci bok trójkąta?
W trójkącie kąt między bokami o długościach 6 i 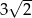 jest równy
jest równy 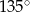 . Jaką długość ma trzeci bok trójkąta?
. Jaką długość ma trzeci bok trójkąta?
W trójkącie 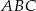 proste zawierające dwusieczne kątów poprowadzonych z wierzchołków
proste zawierające dwusieczne kątów poprowadzonych z wierzchołków 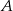 i
i 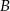 przecinają się pod kątem
przecinają się pod kątem 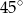 . Wiedząc, że
. Wiedząc, że 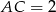 i
i 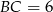 , oblicz
, oblicz
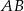 trójkąta
trójkąta 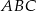 ;
; 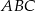 poprowadzonej z wierzchołka
poprowadzonej z wierzchołka 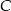 .
.Dane są długości boków  i
i 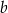 trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku
trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku 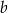 .
.
Trójkąt o bokach 6, 8 i 10 jest podobny do trójkąta o obwodzie 216. Oblicz długości boków drugiego trójkąta.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
W trójkącie 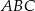 dane są kąty
dane są kąty 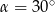 ,
, 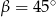 oraz długość
oraz długość  boku leżącego naprzeciw kąta
boku leżącego naprzeciw kąta  . Oblicz długości pozostałych boków.
. Oblicz długości pozostałych boków.
W trójkącie 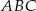 dane są:
dane są: 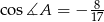 ,
, 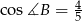 i
i 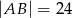 . Oblicz długości pozostałych boków trójkąta
. Oblicz długości pozostałych boków trójkąta 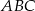 .
.
Liczby 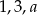 są długościami boków trójkąta. Wyznacz liczbę
są długościami boków trójkąta. Wyznacz liczbę  , wiedząc, że jest to liczba naturalna.
, wiedząc, że jest to liczba naturalna.
Na rysunku przedstawiono trójkąt 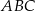 , w którym
, w którym 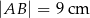 oraz odcinek
oraz odcinek 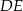 równoległy do boku
równoległy do boku 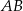 trójkąta.
trójkąta.
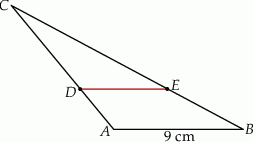
Stosunek pola trapezu 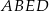 do pola trójkąta
do pola trójkąta 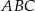 jest równy
jest równy 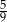 . Oblicz długość odcinka
. Oblicz długość odcinka 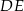 .
.
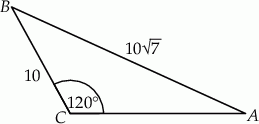
Dany jest trójkąt rozwartokątny 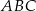 , w którym
, w którym 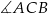 ma miarę
ma miarę 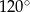 . Ponadto wiadomo, że
. Ponadto wiadomo, że 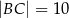 i
i 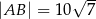 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 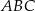 .
.
Dany jest trójkąt 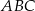 , w którym
, w którym 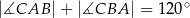 . Ponadto wiadomo, że
. Ponadto wiadomo, że 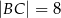 i
i 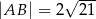 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 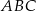 .
.
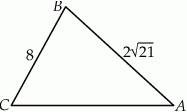
Dany jest trójkąt rozwartokątny 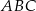 , w którym
, w którym 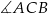 ma miarę
ma miarę 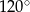 . Ponadto wiadomo, że
. Ponadto wiadomo, że 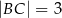 i
i 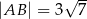 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 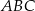 .
.
Kąty ostre trójkąta  o polu
o polu  mają miary
mają miary 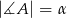 ,
, 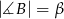 . Oblicz długości boków
. Oblicz długości boków 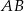 i
i 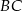 tego trójkąta.
tego trójkąta.
Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy 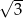 , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
, a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
Punkt 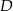 jest środkiem boku
jest środkiem boku 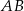 trójkąta
trójkąta 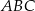 oraz
oraz 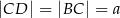 ,
, 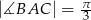 . Oblicz długości boków
. Oblicz długości boków 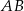 i
i 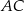 trójkąta
trójkąta 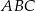 .
.
Wysokość trójkąta 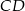 ma długość 4 i dzieli bok
ma długość 4 i dzieli bok 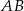 na odcinki, z których krótszy
na odcinki, z których krótszy 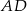 ma długość 2, a kąt
ma długość 2, a kąt 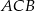 na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku
na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku 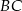 tego trójkąta.
tego trójkąta.
Dane są dwa boki trójkąta: 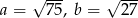 . Jaką długość może przyjmować trzeci bok trójkąta?
. Jaką długość może przyjmować trzeci bok trójkąta?
W trójkącie 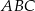 środkowa
środkowa 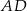 jest prostopadła do boku
jest prostopadła do boku 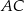 . Kąt
. Kąt 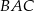 ma miarę
ma miarę 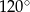 oraz
oraz 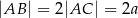 . Oblicz długość odcinka
. Oblicz długość odcinka 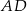 .
.
W trójkącie ostrokątnym 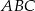 , którego pole równa się 16, boki
, którego pole równa się 16, boki 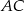 i
i 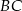 mają długości
mają długości 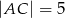 ,
, 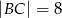 . Oblicz długość boku
. Oblicz długość boku 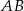 .
.
