Punkty 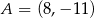 i
i 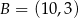 są końcami cięciwy okręgu o środku
są końcami cięciwy okręgu o środku 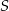 . Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt
. Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt 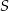 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Różne
Określ wzajemne położenie okręgów 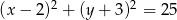 i
i 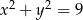 .
.
Określ wzajemne położenie okręgów 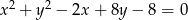 i
i 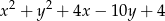 .
.
Określ wzajemne położenie okręgów: 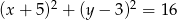 i
i 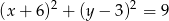 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 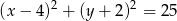 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu 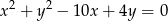 .
.
Wyznacz współrzędne środka i promień okręgu o równaniu 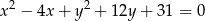 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 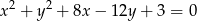 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 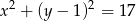 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 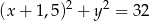 .
.
Okrąg o równaniu 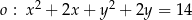 jest styczny do prostych
jest styczny do prostych 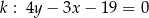 i
i 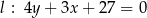 w punktach
w punktach  i
i 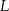 odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu
odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu  , prostych
, prostych 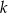 i
i 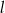 , oraz nie przechodzą przez punkty
, oraz nie przechodzą przez punkty 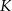 i
i 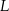 .
.
Określ wzajemne położenie okręgów: 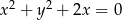 i
i 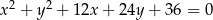 .
.
Znajdź równanie obrazu krzywej 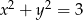 w przesunięciu o wektor
w przesunięciu o wektor ![u = [− 4 ,2 ]](https://img.zadania.info/zad/4910174/HzadT1x.gif) .
.
Oblicz odległość środka okręgu 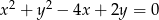 od prostej
od prostej 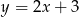 .
.
Punkt 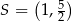 leży wewnątrz figury
leży wewnątrz figury 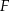 opisanej układem nierówności
opisanej układem nierówności
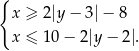
Wyznacz równanie największego okręgu o środku 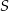 , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury 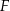 .
.
Napisz równanie okręgu o środku 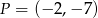 , którego punkty wspólne z okręgiem o równaniu
, którego punkty wspólne z okręgiem o równaniu 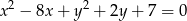 są końcami odcinka o długości
są końcami odcinka o długości 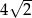 .
.
Okrąg o równaniu 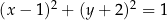 przecina jedną z gałęzi hiperboli o równaniu
przecina jedną z gałęzi hiperboli o równaniu 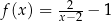 , gdzie
, gdzie 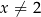 , w punktach
, w punktach 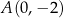 i
i 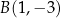 .
.
-
Narysuj obie krzywe we wspólnym układzie współrzędnych.
-
Na drugiej gałęzi hiperboli wyznacz współrzędne takiego punktu
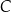 , który jest równo odległy od punktów
, który jest równo odległy od punktów 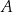 i
i 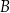 .
.
Dane są figury:
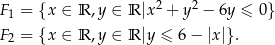
- Narysuj figury
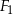 i
i 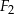 oraz wyznacz figurę
oraz wyznacz figurę 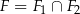 .
. - Oblicz pole figury
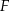
Dane są figury:
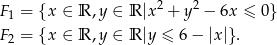
- Narysuj figury
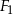 i
i 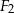 oraz wyznacz figurę
oraz wyznacz figurę 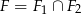 .
. - Oblicz pole figury
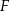
W układzie współrzędnych dany jest okrąg  opisany równaniem
opisany równaniem 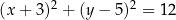 . Sprawdź, czy prosta o równaniu
. Sprawdź, czy prosta o równaniu 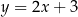 jest styczna do okręgu
jest styczna do okręgu  .
.
Zapisz równanie okręgu o środku 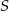 i promieniu
i promieniu  , jeśli
, jeśli 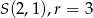 .
.
Zapisz równanie okręgu o środku 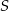 i promieniu
i promieniu  , jeśli
, jeśli 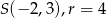 .
.
Dany jest okrąg o równaniu 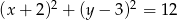 oraz punkt
oraz punkt 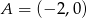 . Napisz równanie symetralnej odcinka, którego końcami są dany punkt
. Napisz równanie symetralnej odcinka, którego końcami są dany punkt 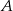 i środek
i środek 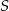 danego okręgu.
danego okręgu.
Sprawdź, czy odległość środka okręgu 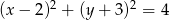 od prostej
od prostej 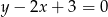 jest równa promieniowi okręgu.
jest równa promieniowi okręgu.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 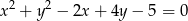 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 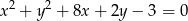 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 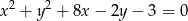 .
.
O ile procent pole koła o promieniu długości 8 jest większe od pola koła wyznaczonego przez okrąg o równaniu 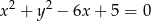 .
.
Środek 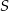 okręgu
okręgu 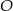 należy do prostej
należy do prostej 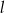 o równaniu
o równaniu 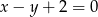 . Punkty
. Punkty 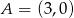 i
i 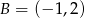 należą do tego okręgu.
należą do tego okręgu.
- Wyznacz równanie okręgu
 .
. - Wyznacz współrzędne takiego punktu
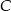 należącego do okręgu
należącego do okręgu 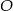 , że
, że 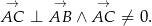
- Wyznacz równania stycznych
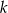 i
i 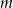 do okręgu
do okręgu 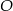 takich, że
takich, że 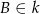 i
i 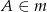 oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
oraz oblicz tangens jednego z kątów, pod jakim przecinają się te styczne.
Okrąg 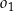 o środku w punkcie
o środku w punkcie 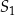 jest określony równaniem
jest określony równaniem 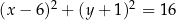 . Okrąg
. Okrąg 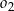 ma środek w punkcie
ma środek w punkcie 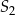 takim, że
takim, że ![−→ S 1S2 = [− 4,4]](https://img.zadania.info/zad/9553446/HzadT5x.png) . Promienie tych okręgów są sobie równe. Figura
. Promienie tych okręgów są sobie równe. Figura 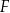 składa się z dwóch okręgów:
składa się z dwóch okręgów: 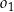 oraz
oraz 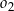 . Punkty
. Punkty 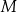 i
i 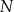 są punktami przecięcia figury
są punktami przecięcia figury 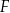 z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt
z tą z jej osi symetrii, która jest prostą o dodatnim współczynniku kierunkowym. Wyznacz punkt 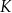 , leżący na jednej z osi symetrii figury
, leżący na jednej z osi symetrii figury 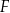 , taki, że pole trójkąta
, taki, że pole trójkąta 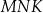 jest równe 40.
jest równe 40.

