Dwa przeciwległe wierzchołki prostokąta mają współrzędne 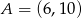 i
i 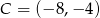 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 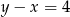 B)
B) 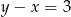 C)
C) 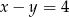 D)
D) 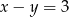
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt/Prostokąt
Jeżeli punkty 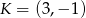 i
i 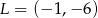 są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
A) 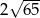 B)
B) 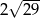 C)
C) 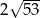 D)
D) 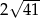
Dłuższy z boków prostokąta 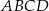 ma długość równą 12, a dwa sąsiednie wierzchołki mają współrzędne
ma długość równą 12, a dwa sąsiednie wierzchołki mają współrzędne 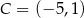 ,
, 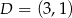 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 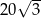 B) 64 C) 80 D) 96
B) 64 C) 80 D) 96
W prostokącie 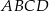 dane są wierzchołki
dane są wierzchołki 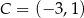 oraz
oraz 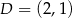 . Bok
. Bok 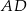 ma długość 6. Pole tego prostokąta jest równe
ma długość 6. Pole tego prostokąta jest równe
A) 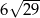 B)
B) 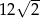 C) 24 D) 30
C) 24 D) 30
Punkty o współrzędnych: 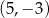 ,
, 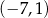 ,
, 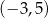 i
i 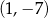 są wierzchołkami prostokąta. Pole tego prostokąta jest równe
są wierzchołkami prostokąta. Pole tego prostokąta jest równe
A) 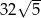 B) 32 C) 64 D)
B) 32 C) 64 D) 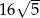
Dany jest prostokąt 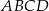 o wierzchołkach
o wierzchołkach 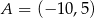 ,
, 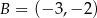 ,
, 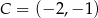 i
i 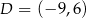 . Który z podanych punktów leży na okręgu opisanym na prostokącie
. Który z podanych punktów leży na okręgu opisanym na prostokącie 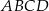 ?
?
A) 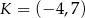 B)
B) 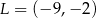 C)
C) 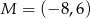 D)
D) 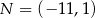
Punkty 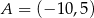 ,
, 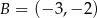 i
i 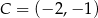 są kolejnymi wierzchołkami prostokąta
są kolejnymi wierzchołkami prostokąta 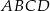 . Wierzchołek
. Wierzchołek 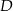 tego prostokąta ma współrzędne
tego prostokąta ma współrzędne
A) 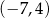 B)
B) 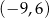 C)
C) 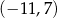 D)
D) 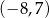
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki prostokąta 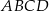 :
: 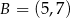 ,
, 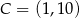 ,
, 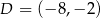 . Jakie współrzędne ma punkt A?
. Jakie współrzędne ma punkt A?
A) 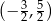 B)
B) 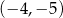 C)
C) 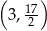 D)
D) 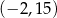
Punkty 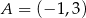 i
i 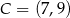 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 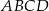 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 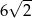 C) 5 D)
C) 5 D) 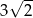
Punkty 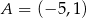 i
i 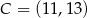 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 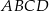 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 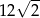 C) 20 D)
C) 20 D) 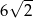
Punkty 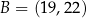 i
i 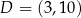 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 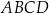 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 20 B) 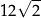 C) 10 D)
C) 10 D) 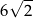
Punkty 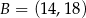 i
i 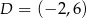 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 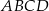 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 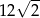 C) 20 D)
C) 20 D) 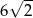
Punkty 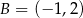 i
i 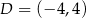 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 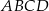 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 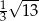 B)
B) 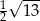 C)
C) 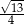 D)
D) 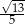
Punkty 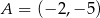 i
i 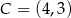 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 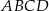 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 8 B) 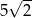 C) 5 D)
C) 5 D) 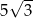
Dwusieczne kątów utworzonych przez przekątne prostokąta 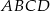 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 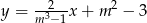 oraz
oraz 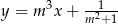 . Zatem
. Zatem
A) 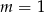 B)
B) 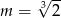 C)
C) 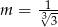 D)
D) 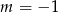
Punkty 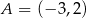 i
i 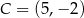 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 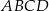 . Długość przekątnej
. Długość przekątnej 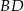 tego prostokąta jest równa
tego prostokąta jest równa
A) 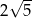 B)
B) 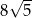 C)
C) 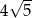 D)
D) 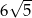
W prostokącie 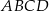 dane są wierzchołki
dane są wierzchołki 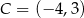 oraz
oraz 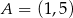 . Bok
. Bok 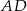 ma długość 3. Pole tego prostokąta jest równe
ma długość 3. Pole tego prostokąta jest równe
A) 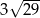 B)
B) 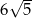 C) 24 D) 18
C) 24 D) 18
W prostokącie 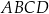 dane są wierzchołki
dane są wierzchołki 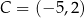 oraz
oraz 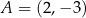 . Bok
. Bok 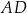 ma długość 5. Pole tego prostokąta jest równe
ma długość 5. Pole tego prostokąta jest równe
A) 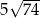 B) 35 C)
B) 35 C) 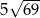 D) 245
D) 245
Punkt 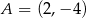 jest wierzchołkiem prostokąta
jest wierzchołkiem prostokąta 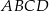 . Prosta o równaniu
. Prosta o równaniu 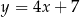 zawiera bok
zawiera bok 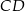 . Bok
. Bok 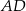 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 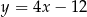 B)
B) 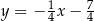 C)
C) 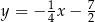 D)
D) 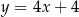
Punkty 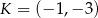 i
i 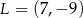 są środkami boków
są środkami boków 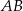 i
i 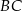 prostokąta
prostokąta 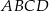 . Boki prostokąta
. Boki prostokąta 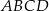 są równoległe do osi układu współrzędnych. Pole prostokąta
są równoległe do osi układu współrzędnych. Pole prostokąta 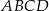 jest równe.
jest równe.
A) 48 B) 20 C) 192 D) 400
Bok 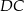 prostokąta
prostokąta 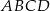 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 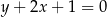 . Jedna z przekątnych tego prostokąta może być zawarta w prostej o równaniu
. Jedna z przekątnych tego prostokąta może być zawarta w prostej o równaniu
A) 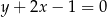 B)
B) 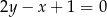 C)
C) 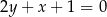 D)
D) 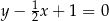
Punkty 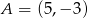 ,
, 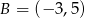 ,
, 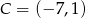 i
i 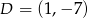 są wierzchołkami prostokąta
są wierzchołkami prostokąta 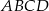 . Pole tego prostokąta jest równe
. Pole tego prostokąta jest równe
A) 16 B) 32 C) 64 D) 96

