Mediana uporządkowanego niemalejąco zestawu liczb: 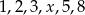 nie zmienia się po dopisaniu liczby 10. Wtedy
nie zmienia się po dopisaniu liczby 10. Wtedy
A) 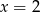 B)
B) 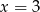 C)
C) 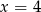 D)
D) 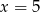
/Szkoła średnia/Zadania testowe/Statystyka/Mediana/Dane z opisu
Wiadomo, że mediana liczb 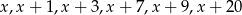 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 5 B) 26 C) 28 D) 4
Wiadomo, że mediana liczb 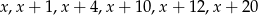 jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 11. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 4 B) 28 C) 22 D) 24
Wiadomo, że mediana liczb 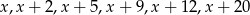 jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
jest równa 9. Zatem suma najmniejszej i największej z tych liczb jest równa
A) 2 B) 16 C) 22 D) 24
Liczba  jest dodatnia. Mediana zestawu czterech liczb:
jest dodatnia. Mediana zestawu czterech liczb: 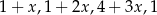 , jest równa 10. Wtedy
, jest równa 10. Wtedy
A) 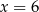 B)
B) 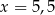 C)
C) 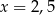 D)
D) 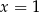
Liczba  jest dodatnia. Mediana zestawu czterech liczb:
jest dodatnia. Mediana zestawu czterech liczb: 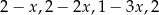 , jest równa
, jest równa 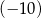 . Wtedy
. Wtedy
A) 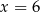 B)
B) 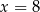 C)
C) 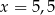 D)
D) 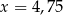
Dany jest zestaw danych: 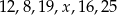 , gdzie
, gdzie  jest pewną liczbą całkowitą. Mediana tego zestawu danych nie może być równa
jest pewną liczbą całkowitą. Mediana tego zestawu danych nie może być równa
A) 14 B) 17,5 C) 13,5 D) 16,5
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 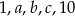 . Mediana liczb:
. Mediana liczb: 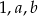 jest równa 3, a mediana liczb:
jest równa 3, a mediana liczb: 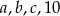 jest równa 5. Liczba
jest równa 5. Liczba  jest równa
jest równa
A) 4 B) 5 C) 6 D) 7
Pięć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej: 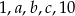 . Mediana liczb:
. Mediana liczb: 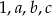 jest równa 3, a mediana liczb:
jest równa 3, a mediana liczb: 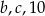 jest równa 8. Liczba
jest równa 8. Liczba 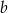 jest równa
jest równa
A) 4 B) 5 C) 6 D) 7
Średnia arytmetyczna dziesięciu liczb naturalnych: 3, 10, 5,  ,
,  ,
,  ,
,  , 12, 19, 7 jest równa 12. Mediana tych liczb jest równa
, 12, 19, 7 jest równa 12. Mediana tych liczb jest równa
A) 14 B) 12 C) 16 D) 
Średnia arytmetyczna zestawu danych: 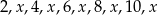 jest równa 4,5. Mediana tego zestawu danych wynosi
jest równa 4,5. Mediana tego zestawu danych wynosi
A) 2 B) 2,5 C) 3 D) 3,5
Średnia arytmetyczna dziesięciu liczb naturalnych: 21, 11, 5,  ,
,  ,
,  ,
,  , 24, 18, 15 jest równa 13. Mediana tych liczb jest równa
, 24, 18, 15 jest równa 13. Mediana tych liczb jest równa
A) 11 B) 9 C) 10 D) 
Sześć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej:
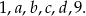
Mediana liczb: 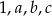 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 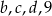 , a średnia arytmetyczna liczb
, a średnia arytmetyczna liczb 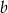 i
i  jest liczbą naturalną. Mediana liczb
jest liczbą naturalną. Mediana liczb 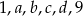 jest równa
jest równa
A) 5 B) 4 C) 6 D) 3
Mediana danych: 0, 1, 1, 2, 3, 1 jest równa
A) 1 B) 1,5 C) 2 D) 2,5
Pięć osób ze sprawdzianu otrzymało ocenę dopuszczającą, cztery dostateczną, trzy osoby ocenę bardzo dobrą, dwie celującą jedna niedostateczną i pięć osób ocenę dobrą. Mediana ocen z tego sprawdzianu jest równa
A) 3 B) 3,5 C) 4 D) 4,5
Wyniki konkursu matematycznego podano w punktach: 94, 92, 90, 90, 86, 86, 86, 72. Medianą tego zestawu wyników jest
A) 86 B) 88 C) 92 D) 94
W czterech rzutach sześcienną kostką do gry otrzymano następujące liczby oczek: 6, 3, 1, 4. Mediana tych danych jest równa
A) 2 B) 2,5 C) 5 D) 3,5
Mediana danych: 1,2,1,1,2,3,1,2,2 jest równa
A) 1 B) 1,5 C) 2 D) 2,5
W kolejnych dziewięciu rzutach kostką otrzymano następujące wyniki: 3, 5, 1, 3, 4, 6, 5, 2, 5. Mediana tych wyników jest równa:
A) 5 B) 4 C) 3,5 D) 3
Pewna firma zatrudnia 6 osób. Dyrektor zarabia 8000 zł, a pensje pozostałych pracowników są równe: 2000 zł, 2800 zł, 3400 zł, 3600 zł, 4200 zł. Mediana zarobków tych 6 osób jest równa
A) 3400 zł B) 3500 zł C) 6000 zł D) 7000 zł
W kolejnych sześciu rzutach kostką otrzymano następujące wyniki: 6, 3, 1, 2, 5, 5. Mediana tych wyników jest równa:
A) 3 B) 3,5 C) 4 D) 5
W loterii liczbowej wylosowano dziesięć liczb: 4, 3, 3, 3, 4, 6, 1, 5, 1, 6. Mediana tych danych jest równa
A) 5 B) 3,6 C) 3,5 D) 3
Pewna firma zatrudnia 7 osób. Dyrektor zarabia 7000 zł, a pensje pozostałych pracowników są równe: 4200 zł, 2800 zł, 2600 zł, 3400 zł, 3600 zł, 3000 zł. Mediana zarobków tych 7 osób jest równa
A) 3400 zł B) 3500 zł C) 3200 zł D) 7000 zł
Mediana danych: 3, 2, 0, 2, 2, 1 jest równa
A) 1 B) 1,5 C) 2 D) 2,5
Wyniki konkursu ortograficznego podano w punktach: 82, 94, 88, 92, 90, 86, 76, 72. Medianą tego zestawu wyników jest
A) 86 B) 88 C) 87 D) 90
W czterech rzutach sześcienną kostką do gry otrzymano następujące liczby oczek: 6, 3, 1, 2. Mediana tych danych jest równa
A) 2 B) 2,5 C) 3 D) 3,5
Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 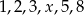 jest równa 4. Wtedy
jest równa 4. Wtedy
A) 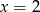 B)
B) 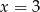 C)
C) 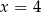 D)
D) 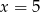
Sześciowyrazowy ciąg liczbowy 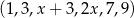 jest niemalejący. Mediana wyrazów tego ciągu jest równa 6. Wynika stąd, że
jest niemalejący. Mediana wyrazów tego ciągu jest równa 6. Wynika stąd, że
A) 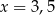 B)
B) 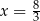 C)
C) 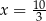 D)
D) 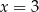
Sześciowyrazowy ciąg liczbowy 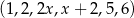 jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że
jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że
A) 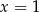 B)
B) 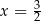 C)
C) 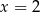 D)
D) 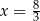
Mediana uporządkowanego niemalejąco zestawu sześciu liczb: 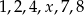 jest równa 5. Wtedy
jest równa 5. Wtedy
A) 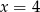 B)
B) 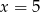 C)
C) 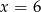 D)
D) 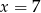
Medianą danych 2,3,3,4,6,7,7,7 jest liczba
A) 4 B) 5 C) 6 D) 7
Medianą danych 2,3,4,5,7,7,7,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Medianą danych 2,3,3,3,5,7,8,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Medianą danych 1,2,3,5,7,7,8,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Mediana kolejnych pięciu liczb naturalnych jest równa 7. Najmniejsza z tych liczb to
A) 5 B) 9 C) 8 D) 11
Mediana kolejnych pięciu liczb naturalnych jest równa 12. Najmniejsza z tych liczb to
A) 16 B) 14 C) 13 D) 10
Mediana kolejnych sześciu liczb naturalnych jest równa 47,5. Najmniejsza z tych liczb to
A) 46 B) 41 C) 45 D) 44
Mediana kolejnych pięciu liczb naturalnych jest równa 8. Najmniejsza z tych liczb to
A) 9 B) 10 C) 6 D) 12
Mediana zestawu liczb: 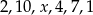 zmniejsza się o 1 po usunięciu liczby
zmniejsza się o 1 po usunięciu liczby  . Wtedy
. Wtedy
A) 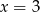 B)
B) 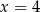 C)
C) 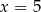 D)
D) 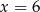
Mediana niemalejącego zestawu danych 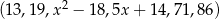 jest równa 40. Zatem
jest równa 40. Zatem
A) istnieją więcej niż dwie możliwe wartości liczby  .
.
B) istnieją dokładnie dwie możliwe wartości liczby  .
.
C) istnieje dokładnie jedna możliwa wartość liczby  .
.
D) nie istnieje liczba  spełniająca podany warunek.
spełniająca podany warunek.
Średnia arytmetyczna zestawu danych:
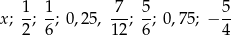
jest równa 0,25. Wtedy mediana tego zestawu danych jest równa
A) 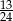 B)
B) 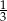 C)
C)  D)
D) 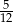
Mediana danych 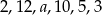 jest równa 7. Wówczas
jest równa 7. Wówczas
A) 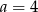 B)
B) 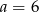 C)
C) 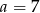 D)
D) 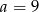
Medianą zestawu danych  jest liczba 4. Wtedy
jest liczba 4. Wtedy  może być równe
może być równe
A) 2 B) 3 C) 4 D) 5
Mediana danych 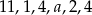 jest równa 3. Wówczas
jest równa 3. Wówczas
A) 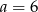 B)
B) 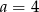 C)
C) 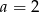 D)
D) 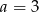
Mediana zestawu sześciu danych liczb: 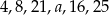 jest równa 14. Zatem
jest równa 14. Zatem
A) 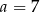 B)
B) 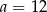 C)
C) 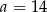 D)
D) 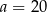
Mediana danych 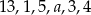 jest równa 4. Wówczas
jest równa 4. Wówczas
A) 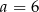 B)
B) 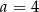 C)
C) 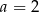 D)
D) 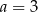
Mediana zestawu ośmiu danych liczb: 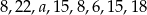 jest równa 14. Zatem
jest równa 14. Zatem
A) 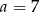 B)
B) 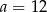 C)
C) 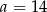 D)
D) 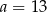
Medianą zestawu danych 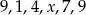 jest liczba 8. Wtedy
jest liczba 8. Wtedy  może być równe
może być równe
A) 8 B) 4 C) 7 D) 9
Sześć liczb: 19, 15, 13,  , 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,
, 7, 1, tworzących zestaw danych, jest uporządkowanych malejąco. Mediana tego zestawu sześciu danych jest równa medianie zestawu pięciu danych: 15,  , 8, 2, 19. Zatem
, 8, 2, 19. Zatem
A) 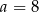 B)
B) 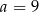 C)
C) 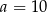 D)
D) 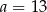
Średnia arytmetyczna zestawu danych: 3, 8, 3, 11, 3, 10, 3,  jest równa 6. Mediana tego zestawu jest równa
jest równa 6. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Średnia arytmetyczna sześciu liczb naturalnych: 31, 16, 25, 29, 27,  , jest równa
, jest równa 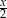 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 26 B) 27 C) 28 D) 29
Średnia arytmetyczna liczb: 3, 1, 6, 5, 2, 4,  , 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
, 2, 3, 8 wynosi 4. Medianą tego zbioru liczb jest
A) 3,5 B) 3 C) 4,5 D) 4
Średnia arytmetyczna sześciu liczb naturalnych: 21, 14, 19, 15, 24,  , jest równa
, jest równa 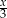 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa
A) 17 B) 20 C) 19 D) 21
Średnia arytmetyczna liczb:  , 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa
, 13, 7, 5, 5, 3, 2, 11 jest równa 7. Mediana tego zestawu liczb jest równa
A) 6 B) 7 C) 10 D) 5
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 12, 14 jest równa 9. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 9 C) 10 D) 16
Średnia arytmetyczna zestawu danych:  , 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
, 2, 4, 6, 8, 10, 13, 16 jest równa 8,5. Wtedy mediana tego zestawu danych jest równa
A) 8 B) 8,5 C) 9 D) 10
Średnia arytmetyczna zestawu danych: 4, 5, 3, 8, 10, 4, 8, 9, 6,  jest równa 6,5. Mediana tego zestawu jest równa
jest równa 6,5. Mediana tego zestawu jest równa
A) 5 B) 6 C) 7 D) 8
Średnia arytmetyczna dziesięciu kolejnych liczb naturalnych jest równa 15,5. Mediana tych liczb jest równa
A) 15,5 B) 31 C) 16 D) 16,5
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
A) 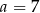 B)
B) 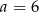 C)
C) 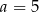 D)
D) 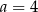
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
A) 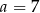 B)
B) 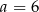 C)
C) 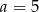 D)
D) 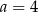
Ze zbioru liczb 3, 4, 1, 5, 1, 3, 1 usunięto jedną liczbę w ten sposób, że mediana tego zbioru liczb nie uległa zmianie. Usunięta liczba to
A) 1 B) 3 C) 4 D) 5

