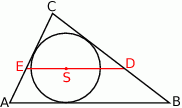
Przez środek 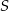 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 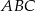 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 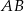 , która przecina boki
, która przecina boki 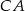 i
i 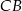 odpowiednio w punktach
odpowiednio w punktach 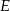 i
i 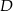 .
.
Wykaż, że 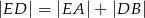 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przez środek  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt  poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku  , która przecina boki
, która przecina boki 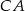 i
i 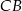 odpowiednio w punktach
odpowiednio w punktach 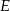 i
i 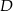 .
.
Wykaż, że 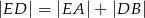 .
.

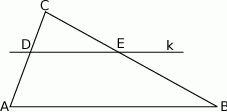
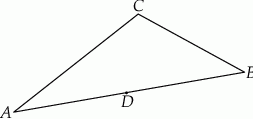
Prosta 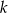 równoległa do boku
równoległa do boku 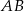 trójkąta
trójkąta 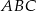 przecina boki
przecina boki 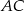 oraz
oraz 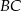 odpowiednio w punktach
odpowiednio w punktach 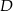 i
i 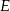 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 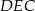 wynosi
wynosi 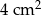 , zaś pole trapezu
, zaś pole trapezu 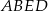 jest równe
jest równe 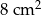 . Wykaż, że
. Wykaż, że 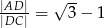 .
.
Prosta  równoległa do boku
równoległa do boku  trójkąta
trójkąta 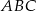 przecina boki
przecina boki 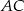 oraz
oraz 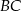 odpowiednio w punktach
odpowiednio w punktach 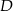 i
i 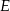 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 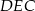 wynosi
wynosi 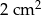 , zaś pole trapezu
, zaś pole trapezu 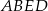 jest równe
jest równe 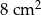 . Wykaż, że
. Wykaż, że 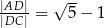 .
.
Dany jest trójkąt 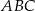 . Punkt
. Punkt 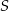 jest środkiem boku
jest środkiem boku 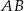 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 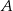 i
i 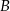 od prostej
od prostej 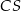 są równe.
są równe.
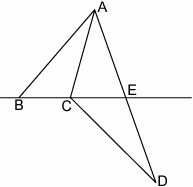
Na boku  trójkąta
trójkąta 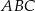 wybrano punkt
wybrano punkt 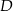 w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 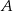 i
i 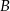 od prostej
od prostej 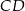 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 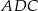 i
i 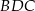 mają równe pola.
mają równe pola.
Pole trójkąta 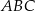 jest równe
jest równe 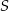 , a długości jego boków
, a długości jego boków 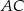 i
i 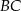 są odpowiednio równe
są odpowiednio równe 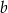 i
i  . Na bokach
. Na bokach 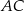 i
i 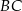 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 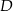 i
i 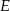 .
.
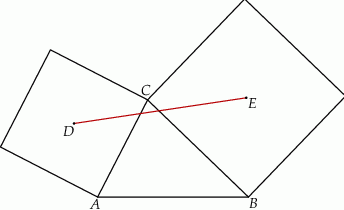
Wykaż, że
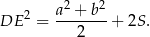
Dane są dwa trójkąty:  oraz
oraz  takie, że
takie, że 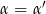 oraz
oraz 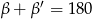 .
.
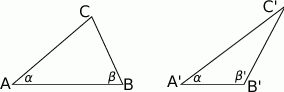
Wykaż, że:
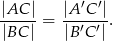
W trójkącie 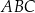 dwusieczna kąta
dwusieczna kąta 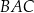 przecina bok
przecina bok 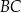 trójkąta w punkcie
trójkąta w punkcie 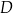 . Wykaż, że
. Wykaż, że
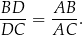
Dany jest trójkąt 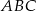 , w którym
, w którym 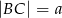 . Z wierzchołka
. Z wierzchołka 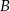 poprowadzono środkową
poprowadzono środkową 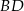 do boku
do boku 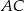 . Punkt
. Punkt 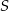 jest środkiem odcinka
jest środkiem odcinka 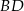 . Przez punkty
. Przez punkty 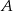 i
i 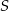 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 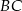 w punkcie
w punkcie 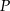 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 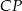 jest równa
jest równa 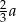 .
.
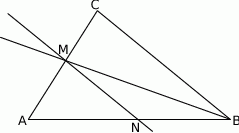
Dany jest trójkąt 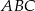 oraz punkt
oraz punkt 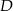 na jego boku
na jego boku 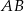 taki, że
taki, że 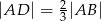 . Z wierzchołka
. Z wierzchołka 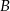 poprowadzono środkową
poprowadzono środkową 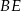 do boku
do boku 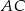 . Punkt
. Punkt 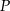 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 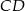 i
i 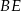 . Wykaż, że punkt
. Wykaż, że punkt 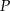 jest środkiem odcinka
jest środkiem odcinka 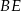 .
.
Wiedząc, że punkt 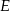 jest środkiem odcinka
jest środkiem odcinka 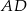 , a punkt
, a punkt 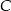 jest środkiem odcinka
jest środkiem odcinka 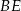 oraz
oraz 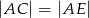 , wykaż, że
, wykaż, że 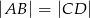 .
.
Odcinki  i
i  są równoległe do boku
są równoległe do boku  trójkąta
trójkąta 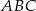 , a odcinki
, a odcinki 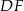 i
i 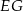 są równoległe do boku
są równoległe do boku 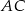 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 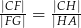 , to
, to 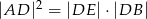 .
.
W trójkącie 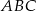 dwusieczna kąta
dwusieczna kąta 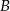 przecina bok
przecina bok 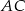 w punkcie
w punkcie 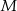 . Przez punkt
. Przez punkt 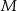 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 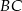 , przecinającą bok
, przecinającą bok 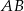 w punkcie
w punkcie 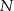 (rys.). Udowodnij, że
(rys.). Udowodnij, że 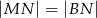 .
.
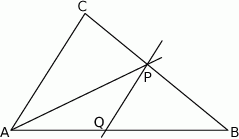
W trójkącie  dwusieczna kąta
dwusieczna kąta  przecina bok
przecina bok  w punkcie
w punkcie 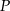 . Przez punkt
. Przez punkt 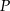 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 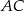 , przecinającą bok
, przecinającą bok 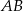 w punkcie
w punkcie 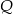 (rys.). Udowodnij, że
(rys.). Udowodnij, że 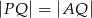 .
.
Wykaż, że jeżeli kąty 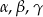 trójkąta
trójkąta 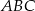 spełniają warunek
spełniają warunek 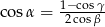 to trójkąt jest równoramienny.
to trójkąt jest równoramienny.
Odcinek 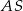 jest środkową trójkąta
jest środkową trójkąta 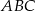 . Udowodnij, że
. Udowodnij, że 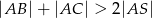 .
.
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.
Wykaż, że jeżeli w trójkącie dwusieczna pokrywa się ze środkową, to trójkąt ten jest równoramienny.
W trójkącie 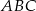 środkowa
środkowa 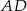 jest prostopadła do boku
jest prostopadła do boku 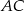 . Kąt
. Kąt 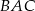 ma miarę
ma miarę 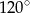 . Wykaż, że
. Wykaż, że 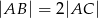 .
.
Środkowa 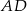 trójkąta
trójkąta 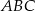 ma długość równą połowie długości boku
ma długość równą połowie długości boku 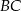 oraz
oraz 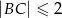 . Wykaż, że
. Wykaż, że 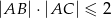 .
.
W trójkącie 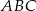 środkowe
środkowe 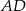 i
i 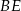 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 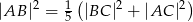 .
.
Dwa boki trójkąta ostrokątnego wpisanego w okrąg o promieniu 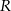 mają długości
mają długości 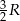 i
i 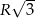 . Wykaż, że długość trzeciego boku wynosi
. Wykaż, że długość trzeciego boku wynosi 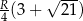 .
.
Trzy cięciwy okręgu o promieniu  tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości
tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości 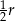 i
i 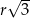 . Wykaż, że trzecia cięciwa ma długość
. Wykaż, że trzecia cięciwa ma długość 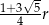 .
.
Wykaż, że jeżeli 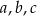 są długościami boków trójkąta to
są długościami boków trójkąta to 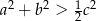 .
.
Na bokach trójkąta zbudowano kwadraty o polach  i
i  (zobacz rysunek)
(zobacz rysunek)
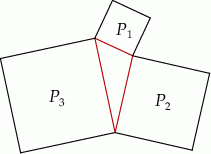
Wykaż, że 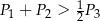 .
.
